湖北省武汉市江夏区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-10 类型：期末考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{a - 1}$ 有意义，则 $a$ 的取值范围是（）

A、 $a \geq 1$ B、 $a \leq 1$ C、 $a > 1$ D、 $a \neq 1$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{\frac{1}{2}} \times \sqrt{6} = \sqrt{3}$ C、 $4 \sqrt{3} - 3 \sqrt{3} = 1$ D、 $\sqrt{{(- 3)}^{2}} = - 3$

查看试题解析
3. 将函数y=﹣3x的图象沿y轴向上平移2个单位长度后，所得图象对应的函数关系式为（）

A、 $y = - 3 x + 2$ B、 $y = - 3 x - 2$ C、 $y = - 3 (x + 2)$ D、 $y = - 3 (x - 2)$

查看试题解析
4. 下列性质中，矩形具有、正方形也具有、但是菱形却不具有的性质是（）

A、对角线互相垂直 B、对角线互相平分 C、对角线长度相等 D、一组对角线平分一组对角

查看试题解析
5. 为了大力宣传节约用电，某小区随机抽查了10户家庭的月用电量情况，统计如下表.关于这10户家庭的月用电量说法正确的是（）

月用电量（度）

25

30

40

50

60

户数

1

2

4

2

1

A、中位数是40 B、众数是4 C、平均数是20.5 D、极差是3

查看试题解析
6. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，过点 $A$ 作 $A E ⊥ B D$ ，垂足为点 $E$ ，若 $∠ E A C = 2 ∠ C A D$ ，则 $∠ B A E =$ （）

A、 $60 °$ B、 $45 °$ C、 $30 °$ D、 $22.5 °$

查看试题解析
7. 对于函数y=－3x＋1，下列结论正确的是（）

A、它的图象必经过点（－1，3） B、它的图象经过第一、二、三象限 C、当x＞ $\frac{1}{3}$ 时，y＜0 D、y的值随x值的增大而增大

查看试题解析
8. 某天早上李雯上学，她先步行一段路程，因为时间紧，她改乘出租车，结果到校还是迟到了5分钟，其行程如图所示，假设这天早上她出门时直乘坐出租车（车速不变），则她（）

A、刚好按时到校 B、可以提前2分钟到校 C、可以提前5分钟到校 D、仍会迟到2分钟到校

查看试题解析
9. 如图所示，在 $Δ A B C$ 中， $A D$ 平分 $∠ C A B$ 交 $B C$ 于点 $E$ ，若 $∠ B D A = 90 °$ ， $E$ 是 $A D$ 中点， $D E = 2$ ， $B D = 3$ ，则 $A C$ 的长为（）

A、 $\frac{5}{3}$ B、 $\frac{4}{3}$ C、 $\frac{3}{2}$ D、1

查看试题解析
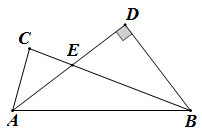10. 如图，在▱ABCD中，CD=2AD，BE⊥AD于点E，F为DC的中点，连结EF、BF，下列结论：①∠ABC=2∠ABF；②EF=BF；③S_{四边形DEBC}=2S_△EFB；④∠CFE=3∠DEF，其中正确结论的个数共有（）

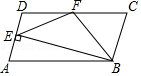A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 计算： $\sqrt{16}$ 的结果为； ${(- \sqrt{5})}^{2}$ 的结果是；在实数范围内因式分解 $x^{3} - 3 x$ 的结果是.

查看试题解析
12. 甲、乙、丙三人进行飞镖比赛，已知他们每人五次投得的成绩如图6－Z－2所示，那么三人中成绩最稳定的是.

查看试题解析
13. 在 $▱ A B C D$ 中， $A B = 5 cm$ ， $∠ A B C$ 的角平分线交对边于一点 $P$ ，若 $\frac{A P}{D P} = \frac{5}{2}$ ，则它的周长为 $cm$ .

查看试题解析
14. 用四块大的正方形地砖和一块小的正方形地砖拼成图所示的实线图案，如果每块大的正方形地砖的面积为 $a$ ，小正方形地砖的面积为 $b$ ，依次连接四块大正方形地砖的一个顶点得到一个正方形 $A B C D$ ，则正方形 $A B C D$ 的面积为.

查看试题解析
15. 如图所示，直线 $y = k x + b (k < 0)$ 经过 $A (3 ， 1)$ ，当 $k x + b \leq \frac{1}{3} x$ 时， $x$ 的取值范围是.

查看试题解析
16. 在 $Δ A B C$ 中， $A B = A C$ ， $∠ B A C = 120 °$ ， $D$ 为 $Δ A B C$ 形内一点，以 $A D$ 为腰作等腰 $Δ D A E$ ，使 $∠ D A E = ∠ B A C$ ，连接 $B E$ 、 $C D$ ，若 $M$ 、 $N$ 分别是 $D E$ 、 $B C$ 的中点， $M N = 1$ ，则 $C D$ 的长为.

查看试题解析

三、解答题

17. 计算：
① $\sqrt{48} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{24}$

② $\frac{2}{3} \sqrt{9 x} + 6 \sqrt{\frac{x}{4}} - 2 x \sqrt{\frac{1}{x}}$

查看试题解析
18. 如图，将平行四边形 $A B C D$ 的对角线 $B D$ 向两个方向延长，分别至点 $E$ 和点 $F$ ，且使 $B E = D F$ .求证：四边形 $A E C F$ 是平行四边形.

查看试题解析
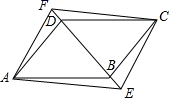19. 在平面直角坐标系中，直线 $y = 3 x + 3$ 分别交 $x$ 轴， $y$ 轴于点 $A ， B$ .

(1)、当 $0 < y \leq 3$ ，自变量 $x$ 的取值范围是（直接写出结果）；

(2)、点 $C (- \frac{2}{3} ， n)$ 在直线 $y = 3 x + 3$ 上.
①直接写出 $n$ 的值为 ▲ ；

②过 $C$ 点作 $C D ⊥ A B$ 交 $x$ 轴于点 $D$ ，求直线 $C D$ 的解析式.

查看试题解析
20. 如图所示，在由边长为1的小正方形成的正方形网格中建立平面直角坐标系，格点 $Δ A B C$ 的顶点坐标分别为 $A (1 ， 6)$ 、 $B (6 ， 6)$ 、 $C (2 ， 2)$ .请仅用无刻度直尺，在给定的网格中依次完成下列作图（要求保留必要的作图痕迹），并回答下列问题：

（ 1 ）画出格点 $A$ 关于直线 $B C$ 的对称点 $D$ ，并写出点 $D$ 的坐标_▲_；

（ 2 ）在 $A B$ 上找到点 $E$ ，使 $∠ A C E = ∠ A B C$ ；

（ 3 ）在 $B D$ 上找到点 $F$ ，使 $B F = B E$ ；

（ 4 ）在 $A C$ 上找到点 $P$ ，使 $B P ⊥ A C$ .直接写出直线 $B P$ 的解析式_▲_.

查看试题解析
21. 如图，点 $G$ 是正方形 $A B C D$ 对角线 $C A$ 的延长线上任意一点，以线段 $A G$ 为边作一个正方形 $A E F G$ ，线段 $E B$ 和 $G D$ 相交于点 $H$ .

(1)、求证： $△ E A B ≅ △ G A D$ ；

(2)、若 $A B = 3 \sqrt{2}$ ， $A G = 3$ ，求 $E B$ 的长.

查看试题解析
22. 在2019年春季环境整治活动中，某社区计划对面积为 $1600 m^{2}$ 的区域进行绿化.经投标，由甲、乙两个工程队来完成，若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍，并且在独立完成面积为 $400 m^{2}$ 区域的绿化时，甲队比乙队少用5天.

(1)、求甲、乙两工程队每天能完成绿化的面积；

(2)、设甲工程队施工 $x$ 天，乙工程队施工 $y$ 天，刚好完成绿化任务，求 $y$ 关于 $x$ 的函数关系式；

(3)、在（2）的条件下，若甲队每天绿化费用是0.6万元，乙队每天绿化费用为0.25万元，且甲乙两队施工的总天数不超过25天，则如何安排甲乙两队施工的天数，使施工总费用最低？并求出最低费用.

查看试题解析
23. 矩形 $A B C D$ 中， $A B = 6$ ， $A D = 8$ ， $E$ 是 $B C$ 边上一点， $E F ⊥ A E$ 且 $E F = A E$ .

(1)、如图1，当 $F$ 在 $C D$ 边上时，求 $B E$ 的长；

(2)、如图2，若 $D F ⊥ E F$ ，求 $\frac{B E}{B C}$ 的值；

(3)、如图3， $Q$ 为 $A F$ 的中点，直接写出 $C Q$ 的最小值为.

查看试题解析
24. 如图1，直线 $y = - \frac{1}{2} x + 2$ 与 $x$ 轴、 $y$ 轴分别交于 $A$ 、 $B$ 两点，点 $E$ 为 $y$ 轴负半轴上一点，且 $S_{Δ A B E} = 12$ .

(1)、求直线 $A E$ 的解析式；

(2)、如图2，直线 $y = m x$ 交直线 $A B$ 于点 $M$ ，交直线 $A E$ 于点 $N$ ，当 $S_{Δ O E N} = 2 S_{Δ O B M}$ 时，求 $m$ 的值；

(3)、如图3，点 $P$ 为直线 $y = - x - 1$ 上一点，若 $∠ A B P = 45 °$ ，请直接写出点 $P$ 的坐标：.

查看试题解析

月用电量（度）	25	30	40	50	60
户数	1	2	4	2	1