湖北省武汉市江汉区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-10 类型：期末考试

进入出卷网下载

一、单选题

1. 使 $\sqrt{a - 1}$ 有意义的a的取值范围是（）

A、a＞1 B、a≤1 C、a＜1 D、a≥1

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{3} = \sqrt{6}$ B、 $\sqrt{7} - \sqrt{2} = \sqrt{5}$ C、 $2 \times \sqrt{5} = \sqrt{10}$ D、 $\sqrt{8} \div 2 = \sqrt{2}$

查看试题解析
3. 下列长度的三条线段，不能组成直角三角形的是（）

A、1， $\sqrt{2}$ ， $\sqrt{3}$ B、5，12，13 C、0.3，0.4，0.5 D、 $3^{2}$ ， $4^{2}$ ， $5^{2}$

查看试题解析
4. 下列函数是正比例函数的是（）

A、 $y = \frac{x}{2}$ B、 $y = \frac{2}{x}$ C、 $y = x^{2}$ D、 $y = 2 (x + 1)$

查看试题解析
5. 下列图象中，能表示y是x的函数的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 甲、乙、丙、丁四位同学五次数学测验成绩统计如表．如果从这四位同学中，选出一位成绩较好且状态稳定的同学参加全国数学联赛，那么应选（）
甲
乙
丙
丁
平均数
80
85
85
80
方差
42
42
54
59

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 下列说法正确的是（）

A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相垂直且相等的四边形是正方形 D、每组邻边都互相垂直且相等的四边形是正方形

查看试题解析
8. 如图，在矩形ABCD中，AD=10，AB=6，E为BC上一点，DE平分∠AEC，则CE的长为（）

A、1 B、2 C、3 D、4

查看试题解析
9. 若一次函数 $y = k x + b$ （k，b是常数）的图象不经过第三象限，则一次函数 $y = x + k b$ 的图象（）

A、不经过第二象限 B、不经过第四象限 C、经过一、二、三象限 D、经过一、三、四象限

查看试题解析
10. 如图，点P是正方形 $A B C D$ 的对角线 $B D$ 上一点， $P E ⊥ B C$ ， $P F ⊥ C D$ ，垂足分别为E，F，连接 $A P$ ， $E F$ ，下列结论：① $A P = E F$ ；② $A P ⊥ E F$ ；③ $△ A P D$ 与四边形 $P E F D$ 的面积相等.其中正确的结论是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题

11. 计算： $\sqrt{{(- 4)}^{2}}$ = ．

查看试题解析
12. 已知一组数据5，7，9，4，－1，则这组数据的中位数是.

查看试题解析
13. 将直线 $y = 2 x + 3$ 向下平移5个单位长度，则平移后的直线解析式为.

查看试题解析
14. 如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为 $8 c m$ ，则图中所有正方形的面积的和是 $c m^{2}$ .

查看试题解析
15. 在平面直角坐标系 $x O y$ 中，一次函数 $y = k x$ 和 $y = m x + n$ 的图象如图所示，则关于x的一元一次不等式 $(k - m) x - n > 0$ 的解集是.

查看试题解析
16. 如图，在四边形 $A B C D$ 中， $A B = A D$ ， $∠ A = ∠ C = 90 °$ ，若 $B C + C D = 10 cm$ ，则四边形 $A B C D$ 的面积为 ${cm}^{2}$ .

查看试题解析
17. 函数 $y = | 2 x + 1 | - 2$ 的图象如图，当 $- 2 < x < 2$ 时，则函数值y的取值范围是.

查看试题解析
18. 已知一次函数 $y = (m - 1) x - 2 m + 5$ 图象上两点 $A (x_{1} ， y_{1})$ 和 $B (x_{2} ， y_{2})$ ，下列结论：①若 $(x_{1} - x_{2}) (y_{1} - y_{2}) < 0$ ，则 $m < 1$ ；②图象过定点 $(2 ， 3)$ ；③原点O到直线 $A B$ 的距离的最大值为5，正确的是（填写正确结论的序号）.

查看试题解析
19. 如图，在边长为4的正方形 $A B C D$ 中，E是 $B C$ 的中点，F是 $C D$ 上一点， $D F = 1$ ，连 $A E$ ， $B F$ ，P，Q分别为 $A E$ 和 $B F$ 的中点，则 $P Q =$ .

查看试题解析
20. 如图，P是正方形 $A B C D$ 内一点， $C P = C D$ ， $A P ⊥ B P$ ，则 $\frac{P A}{P D}$ 的值为.

查看试题解析

三、解答题

21. 计算下列各题：

(1)、 $\sqrt{75} \times \sqrt{\frac{1}{3}} \div \sqrt{5}$

(2)、 $\sqrt{18} + \sqrt{12} - \sqrt{\frac{1}{2}} - \sqrt{27}$ .

查看试题解析
22. 某校为了解学生每天在校体育活动的时间（单位： $h$ ），随机调查了该校的部分学生，根据调查结果绘制出如图所示的统计图.

(1)、求被调查的学生人数为， $m =$ ；

(2)、求被调查的学生每天在校体育活动时间的平均数、众数；

(3)、若该校有1500名学生，估计该校每天在校体育活动时间大于 $1 h$ 的学生人数.

查看试题解析
23. 已知，在边长为1的小正方形组成的 $4 \times 8$ 网格中， $△ A B C$ 的顶点均为格点.，请按要求分别作出 $△ A B C$ ，并解答问题.

(1)、在图1中作钝角 $△ A B C$ ，图2中作直角 $△ A B C$ ，图3中作锐角 $△ A B C$ ，都使 $B C = 5$ ；

(2)、在图4中作直角 $△ A B C$ ， $A B$ 为斜边，两直角边长度为无理数，并直接写出 $△ A B C$ 的面积.

查看试题解析
24. 如图，菱形 $A B C D$ 的对角线 $A C$ ， $B D$ 交于点O，过点B作 $B E // A C$ ，且使得 $B E = \frac{1}{2} A C$ ，连接 $E C$ ， $E D$ .

(1)、求证：四边形 $B E C O$ 是矩形

(2)、若 $A C = 2$ ， $∠ A B C = 60 °$ ，求 $D E$ 的长.

查看试题解析
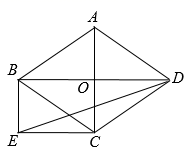25. 已知一次函数 $y = k x + b$ 的图象过点 $(1 ， 4)$ 和 $(- 1 ， 8)$ .且交x轴于点A，交y轴于点B.

(1)、求这个函数的解析式；

(2)、求 $△ A O B$ 的面积

(3)、已知点 $M (6 ， - 2)$ ，点 $N (0 ， 2)$ ，点 $P (m ， n)$ 在线段 $A B$ 上，设 $△ P M N$ 的面积为S，请直接写出S关于m的函数关系式以及自变量m的取值范围.

查看试题解析
26. A城有肥料400吨，B城有肥料600吨.现要把这些肥料全部运往C，D两乡，C乡需要肥料480吨，D乡需要肥料520吨，其运往C，D两乡的运费如下表：

运往C乡

运往D乡

A城

20元/吨

18元/吨

B城

16元/吨

12元/吨

设从A城运往C乡的肥料为x吨，从A城运往两乡的总运费为 $y_{1}$ 元，从B城运往两乡的总运费为 $y_{2}$ 元.

(1)、分别求 $y_{1}$ ， $y_{2}$ 与x之间的函数关系式，以及同时满足 $y_{1}$ ， $y_{2}$ 的自变量x的取值范围；

(2)、若A城的总运费不得超过7600元，怎样调运使两城总费用的和最少？并求出最小值.

查看试题解析
27. 如图，P是正方形 $A B C D$ 的边 $C D$ 右侧一点， $C P = C D$ ， $∠ P C D$ 为锐角，连 $P B$ ， $P D$ .

(1)、如图1，若 $P D = P C$ ，则 $∠ B P D$ 的度数为；

(2)、如图2，作 $C E$ 平分 $∠ P C D$ 交 $P B$ 于E.
①求 $∠ B E C$ 的度数；

②猜想 $P D$ ， $B E$ ， $C E$ 之间有何数量关系，并证明你的结论；

(3)、如图3，若 $P B = 6$ ，则四边形 $P C B D$ 的面积为平方单位

查看试题解析
28. 如图，在平面直角坐标系中，直线l交x轴负半轴于 $A (a ， 0)$ ，交y轴于 $B (0 ， 1)$ ，且 $∠ B A O = 30 °$ ，C是x轴正半轴上一点，且点C关于直线l的对称点D正好落在y轴上.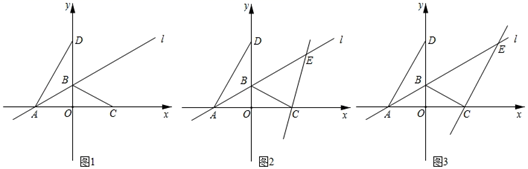

(1)、直接写出
① $a =$ .

②直线 $l$ 的解析式为.

③C点的坐标.

(2)、点E为直线l上一点，且在第一象限内
①如图2，若 $∠ A E C = 45 °$ ，求E点坐标

②如图3，若直线 $C E$ 的解析式为 $y = \frac{4}{3} \sqrt{3} x + b$ ，P是直线 $C E$ 上位于y轴右侧的一点，点Q在y轴上，当 $△ C P Q$ 为等边三角形时，直接写出P点的坐标.

查看试题解析

	运往C乡	运往D乡
A城	20元/吨	18元/吨
B城	16元/吨	12元/吨

	甲	乙	丙	丁
平均数	80	85	85	80
方差	42	42	54	59