湖北省武汉市洪山区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-10 类型：期末考试

进入出卷网下载

一、单选题

1. 一次函数 $y = - 2 x - 3$ 的图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列计算错误的是（）

A、 $\sqrt{12} \times \sqrt{\frac{3}{4}} = 3$ B、 $2 \sqrt{2} - \sqrt{2} = \sqrt{2}$ C、 $\sqrt{16} = \pm 4$ D、 $(\sqrt{2} + \sqrt{3}) - \sqrt{3} = \sqrt{2}$

查看试题解析
3. 2021年8月18日，第三十一届世界大学生夏季运动会将在四川成都举行.为迎接大运会的到来，某校开展了主题为“爱成都•迎大运”的演讲比赛.九年级10名同学参加该演讲比赛的成绩如下表，则这组数据的众数和中位数分别为（）

成绩/分

80

85

90

95

人数/人

2

3

4

1

A、 85，87.5 B、85，85 C、90，85 D、90，87.5

查看试题解析
4. 已知 $A (- \frac{1}{3} ， y_{1})$ ， $B (- 1 ， y_{2})$ ， $C (\frac{1}{2} ， y_{3})$ 是一次函数 $y = - x + b$ 的图象上的三点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系为（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{1} < y_{2}$ C、 $y_{3} < y_{2} < y_{1}$ D、 $y_{2} < y_{1} < y_{3}$

查看试题解析
5. 四边形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 交于 $O$ ，下列条件不能判定四边形 $A B C D$ 是菱形的是（）

A、 $∠ A B C = ∠ A D C$ ， $∠ B A D = ∠ B C D$ ， $A C ⊥ B D$ B、 $A B // C D$ ， $A B = C D$ ， $A B = B C$ C、 $O A = O C$ ， $O B = O D$ ， $A C ⊥ B D$ D、 $A B // C D$ ， $A D = B C$ ， $A B = B C$

查看试题解析
6. 将函数 $y = 3 x$ 的图象沿y轴向下平移4个单位长度后所得图象的函数关系式为（）

A、 $y = - 3 (x - 4)$ B、 $y = - 3 x - 4$ C、 $y = - 3 (x + 4)$ D、 $y = 3 x - 4$

查看试题解析
7. 如图，点 $E$ 为 $▱ A B C D$ 边 $A D$ 上一点，将 $△ A B E$ 沿 $B E$ 翻折得到 $△ F B E$ ，点 $F$ 在 $B D$ 上，且 $E F = D F$ . $∠ C = 52 °$ 那么 $∠ A B E$ 的度数为（）

A、38° B、48° C、51° D、62°

查看试题解析

8. 某登山队大本营所在地的气温为5℃，气温随着海拔高度增加而下降.已知登山队所在的位置的气温是y（单位：℃），登山队员由大本营向上登高x（单位：km），则y是x的一次函数.下表记录了四次测量的数据，其中只有一组是记录错误的数据，它是（）

组数	第一组	第二组	第三组	第四组
x	1	2	4	5
y	－1	－7	－15	－25

A、第一组 B、第二组 C、第三组 D、第四组

查看试题解析

9. 如图1，将正方形 $A B C D$ 置于平面直角坐标系中，其中 $A D$ 边在x轴上，其余各边均与坐标轴平行，直线 $L ： y = x - 3$ 沿x轴的负方向以每秒1个单位的速度平移，在平移的过程中，该直线被正方形 $A B C D$ 的边所截得的线段长为m，平移的时间为t（秒），m与t的函数图象如图2所示，则图2中a的值为（）

A、7 B、9 C、12 D、13

查看试题解析
10. 如图，矩形 $A B C D$ 中， $A E ⊥ B D$ 交 $C D$ 于点 $E$ ，点 $F$ 在 $A D$ 上，连接 $C F$ 交 $A E$ 于点 $G$ ，且 $C G = G F = A F$ ，若 $B D = 4 \sqrt{3}$ ，则 $C D$ 的值为（）

A、 $\sqrt{15}$ B、4 C、 $\sqrt{17}$ D、 $\sqrt{30}$

查看试题解析

二、填空题

11. 二次根式 $\sqrt{2 - 3 x}$ 有意义，则x的取值范围是

查看试题解析
12. 某中学八年级开展“光盘行动”宣传活动，6个班级参加该活动的人数统计结果为：28，32，31，27，29，32，对于这组统计数据的中位数是

查看试题解析
13. 如图，已知一次函数 $y_{1} = x + b$ 与正比例函数 $y_{2} = k x$ 的图象交于点 $P$ .四个结论：① $k > 0$ ；② $b > 0$ ：③当 $x < 0$ 时， $y_{2} > 0$ ；④当 $x < - 2$ 时， $k x > x + b$ .其中正确的是（填写序号）

查看试题解析
14. 甲、乙两车同时从A地出发，以各自的速度匀速向B地行驶．甲车先到达B地后，立即按原路以相同速度匀速返回（停留时间不作考虑），直到两车相遇．若甲、乙两车之间的距离y（千米）与两车行驶的时间x（小时）之间的函数图象如图所示，则A，B两地之间的距离为千米．

查看试题解析
15. 已知在平面直角坐标系中， $A (3 ， 2)$ ，点 $C$ 在 $x$ 轴上，当 $k$ 变化时，一次函数 $y = (k - 3) x + k$ 都经过一定点 $B$ ，则 $C A + C B$ 最小值为

查看试题解析
16. 如图，在矩形 $A B C D$ 中， $A B = 2$ ， $A D = 4$ ， $E$ 为 $A D$ 的中点， $F$ 为线段 $E C$ 上一动点， $P$ 为 $B F$ 中点，连接 $P D$ ，则线段 $P D$ 长的取值范围是

查看试题解析

三、解答题

17. 解答下列各题

(1)、计算： $\sqrt{8} + \sqrt{27} - (\sqrt{2} + 2 \sqrt{3})$

(2)、已知一次函数 $y = k x + b$ 的图象经过点 $(3 ， 5)$ 与 $(- 4 ， - 9)$ ，求一次函数的解析式.

查看试题解析
18. 已知，如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G．

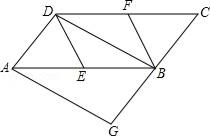(1)、求证：四边形AGBD为平行四边形；

(2)、若四边形AGBD是矩形，则四边形BEDF是什么特殊四边形？证明你的结论．

查看试题解析

19. 为了加强学生课外阅读，开阔视野，某校开展了“书香校园，诵读经典”竞赛活动，学校2000名学生全部参加了竞赛，结果所有学生成绩都不低于60分（满分100分）.为了了解成绩分布情况，学校随机抽取了部分学生的成绩进行统计，得到如下不完整的统计表.根据表中所给信息，解答下列问题：

组别	成绩	人数
A	$90 \leq x \leq 100$	16
B	$80 \leq x < 90$	a
C	$70 \leq x < 80$	b
D	$60 \leq x < 70$	10

(1)、这次被调查的同学共有人，

a =

(2)、本次竞赛随机抽取的部分学生成绩组成的一组数据的中位数落在组，扇形统计图中“

B

组”所对应的圆心角的度数是°

(3)、若成绩不小于80分为优秀，请你估计该校学生大约有多少名学生获得优秀成绩.

查看试题解析

20. 如图，在每个小正方形的边长为1的格中，点 $C ， D ， E ， F ， G$ 均在格点上， $D E$ 与 $F G$ 相交于点 $T$

(1)、 $C D$ 的长等于

(2)、在如图所的网格中，用无刻度的直尺，画出以 $D E$ 为一边的正方形以 $C D ， D T$ 为邻边的矩形 $C D T P$

查看试题解析
21. 在平面直角坐标系中，一次函数 $y = k x + b$ 和 $y = - x + 4$ 的图象分别与 $x$ 轴相交于A、B两点，且这两条直线的交点为C.已知A点坐标为 $(- 1 ， 0)$

(1)、当点C的横坐标是2时，直接写出不等式 $0 < k x + b \leq 2$ 的解集为；

(2)、当点C的横坐标是－2时，求 $△ A B C$ 的面积；

(3)、当 $- 2 < x \leq 2$ 时，直线 $y = k x - 4$ 和 $y = - x - b$ 有交点，直接写出k的取值范围.

查看试题解析
22. 2020年新冠肺炎疫情发生以来，每天用消毒液进行消毒成为一种习惯.某经销店经销甲、乙两种规格复合型消毒液，如下表所示是该店甲、乙两种复合型消毒液的进价和售价：

商品价格

甲种规格

乙种规格

进价（元/瓶）

40

100

售价（元/瓶）

45

110

该店现有一批用7600元购进的甲、乙两种规格复合型消毒液库存，预计全部销售后，可获毛利润共800元.[毛利润＝（售价－进价）×销售量]

(1)、该店库存的甲、乙两种规格复合型消毒液分别为多少瓶？

(2)、根据销售情况，该经销店计划在进价不变情况下，用不超过8000元的资金购进这两种规格复合型消毒液，在原进货数量上，增加甲种规格复合型消毒液的购进量，减少乙种规格复合型消毒液的购进量.已知甲种规格复合型消毒液增加的数量是乙种规格复合型消毒液减少的数量的3倍，则该店怎样进货，可使这次进货全部销售后获得的毛利润最大？并求出最大毛利润.

查看试题解析
23. 正方形 $A B C D$ 中，点 $E$ 、 $F$ 分别在 $A B$ 、 $D C$ 上动点（与顶点不重合），且满足 $A E = C F$

(1)、如图1，连 $E F$ 与对角线 $B D$ 交于点 $O$ ，求证 $O E = O F$

(2)、如图2，连 $D E$ ，过点 $F$ 作 $B C$ 的平行线，分别交 $A C$ 、 $A B$ 于点M、G.过点M作 $H M ⊥ A C$ 交 $A B$ 的延长线于点 $H$ ，连 $H C$ 、 $B M$ ，若 $H C // D E$ ，判断 $D E$ 与 $B M$ 的数量关系，并加以证明.

(3)、如图3，过点 $B$ 作 $B K ⊥$ 直线 $E F$ ，垂足为 $K$ 点，连 $K C$ ，若正方形边长为8，则线段 $K C$ 的最大值为.

查看试题解析
24. 如图在平面直角坐标系之中，点 $O$ 为坐标原点，直线 $y = - \frac{3}{4} x + 3$ 分别交x、y轴于点 $B$ 、 $A$ .

(1)、如图1，点 $C$ 是直线 $A B$ 上不同于点 $B$ 的点，且 $C A = A B$ .则点 $C$ 的坐标为

(2)、点 $C$ 是直线 $A B$ 外一点，满足 $∠ B A C = 45 °$ ，求出直线 $A C$ 的解析式.

(3)、如图2，点 $D$ 是线段 $O B$ 上一点，将 $△ A O D$ 沿直线 $A D$ 翻折，点 $O$ 落在线段 $A B$ 上的点E处，点M在射线 $D E$ 上，在x轴的正半轴上是否存在点N，使以M、A、N、B为顶点的四边形是平行四边形？若存在，请求出点N的坐标；若不存在，请说明理由.

查看试题解析

商品价格	甲种规格	乙种规格
进价（元/瓶）	40	100
售价（元/瓶）	45	110

成绩/分	80	85	90	95
人数/人	2	3	4	1