湖北省武汉市汉阳区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-08-10 类型:期末考试
一、单选题
-
1. 若式子 在实数范围内有意义,则x的取值范围是( )A、x≠1 B、x≤1 C、x≥1 D、x<12. 下列计算正确的是( )A、 B、 C、 D、3. 一组数据4,6,5,5,10中,平均数是( )A、5 B、6 C、7 D、84. 如图,在高为 ,坡面长为 的楼梯表面铺地毯,地毯的长度至少需要( )
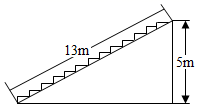 A、 B、 C、 D、5. 下列关于四边形的说法,正确的是( )A、四个角都是直角的四边形是正方形 B、对角线互相垂直的四边形是菱形 C、有两边相等的平行四边形是菱形 D、两条对角线相等的菱形是正方形6. 某次数学素养大赛选拔赛,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.学校将八班同学的成绩整理并绘制成如下统计图,根据统计图可知该组数据的中位数是( )
A、 B、 C、 D、5. 下列关于四边形的说法,正确的是( )A、四个角都是直角的四边形是正方形 B、对角线互相垂直的四边形是菱形 C、有两边相等的平行四边形是菱形 D、两条对角线相等的菱形是正方形6. 某次数学素养大赛选拔赛,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.学校将八班同学的成绩整理并绘制成如下统计图,根据统计图可知该组数据的中位数是( )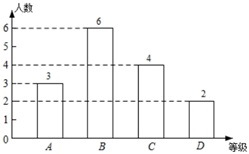 A、100分 B、90分 C、80分 D、70分7. 对于函数 ,下列结论正确的是( )A、它的图象必经过点 B、它的图象不经过第三象限 C、当 时, D、 随 的增大而增大8. 1903年,英国物理学家卢瑟福通过实验证实,放射性物质在放出射线后,这种物质的质量将减少,减少的速度开始较快,后来较慢,实际上,放射性物质的质量减为原来的一半所用的时间是一个不变的量,我们把这个时间称为此种放射性物质的半衰期.如图是表示镭的放射规律的函数图象,根据图象可以判断,镭的质量衰减到 ( 为正整数)的时间是( )
A、100分 B、90分 C、80分 D、70分7. 对于函数 ,下列结论正确的是( )A、它的图象必经过点 B、它的图象不经过第三象限 C、当 时, D、 随 的增大而增大8. 1903年,英国物理学家卢瑟福通过实验证实,放射性物质在放出射线后,这种物质的质量将减少,减少的速度开始较快,后来较慢,实际上,放射性物质的质量减为原来的一半所用的时间是一个不变的量,我们把这个时间称为此种放射性物质的半衰期.如图是表示镭的放射规律的函数图象,根据图象可以判断,镭的质量衰减到 ( 为正整数)的时间是( )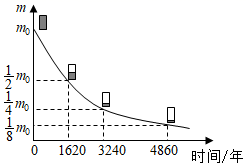 A、 年 B、 年 C、 年 D、 年9. 弹簧秤是重要的计重工具.弹簧挂上物体后会伸长,设弹簧所挂的物体的质量 时,弹簧的长度 ,并且 是 的一次函数.下表记录了四次称重的数据,其中有一组数据记录错误,它是( )
A、 年 B、 年 C、 年 D、 年9. 弹簧秤是重要的计重工具.弹簧挂上物体后会伸长,设弹簧所挂的物体的质量 时,弹簧的长度 ,并且 是 的一次函数.下表记录了四次称重的数据,其中有一组数据记录错误,它是( )组数
1
2
3
4
1
2
5
7
20.5
22
25.5
29.5
A、第1组 B、第2组 C、第3组 D、第4组10. 如图, 、 是正方形 的边 上的两个动点,满足 ,连接 交 于点 ,连接 交 于点 ,连接 ,若正方形的边长为2,则线段 的最小值是( )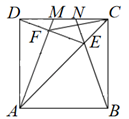 A、2 B、1 C、 D、
A、2 B、1 C、 D、二、填空题
-
11. 把直线y=-2x+1向下平移3个单位后得到直线.12. 已知一次函数的图象经过 , 两点,则该一次函数解析式是.13. 甲,乙,丙,丁四位同学10次数学测验成绩统计如右表所示,如果从这四位同学中,选出一位平均成绩高且成绩稳定的同学参加数学竞赛,那么应选去.
甲
乙
丙
丁
平均分/分
86
90
90
85
方差
24
36
42
38
14. 在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图BD是平行四边形ABCD的对角线,点E在BD上,DC=DE=AE,∠1=25°,则∠C的大小是. 15. 一次函数 与 的图象如图所示,下列说法:①函数 中 随 的增大而减小;②函数 经过第一、二、四象限;③不等式 的解集是 ;④ .其中正确的是(只填序号).
15. 一次函数 与 的图象如图所示,下列说法:①函数 中 随 的增大而减小;②函数 经过第一、二、四象限;③不等式 的解集是 ;④ .其中正确的是(只填序号).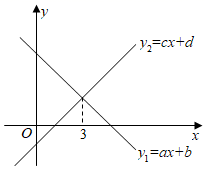 16. 甲、乙两车从 城出发前往 城.在整个行程中,汽车离开 城的距离 与时刻 的对应关系如图所示,则甲、乙两车相距 时,对应 的值是.
16. 甲、乙两车从 城出发前往 城.在整个行程中,汽车离开 城的距离 与时刻 的对应关系如图所示,则甲、乙两车相距 时,对应 的值是.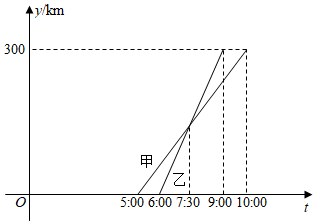
三、解答题
-
17. (模型建立)如图1,等腰直角三角形 中, , ,直线 经过点 ,过点 作 于点 ,过点 作 于点 ,易证明 (无需证明),我们将这个模型称为“ 形图”.接下来我们就利用这个模型来解决一些问题:
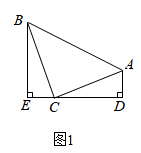 (1)、(模型运用)
(1)、(模型运用)如图2,在平面直角坐标系中,等腰 , , , 与 轴交点 ,点 的坐标为 , 点的坐标为 ,求 , 两点坐标;
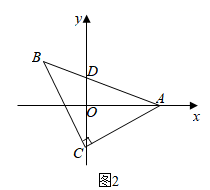 (2)、如图3,在平面直角坐标系中,直线 函数关系式为: ,它交 轴于点 ,交 轴于点 ,在 轴上是否存在点 ,使直线 与直线 的夹角为45°?若存在,求出点 的坐标;若不存在,请说明理由.
(2)、如图3,在平面直角坐标系中,直线 函数关系式为: ,它交 轴于点 ,交 轴于点 ,在 轴上是否存在点 ,使直线 与直线 的夹角为45°?若存在,求出点 的坐标;若不存在,请说明理由.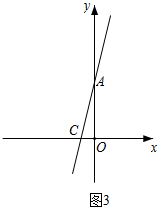 (3)、(模型拓展)
(3)、(模型拓展)如图4,在 中, , , ,点 在 上,点 在 上, ,分别连接 , 交于 点.若 ,请直接写出 的长.
 18. 计算:(1)、 ;(2)、 .19. 如图, , 分别是平行四边形 的边 , 边上的点,且 ,连接 , .求证:四边形 是平行四边形.
18. 计算:(1)、 ;(2)、 .19. 如图, , 分别是平行四边形 的边 , 边上的点,且 ,连接 , .求证:四边形 是平行四边形.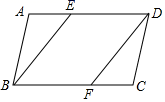 20. 某中学要从八年级学生中选报一名学生参加数学知识竞赛,需要从获奖情况、笔试、面试三个项目进行综合考查,按获奖情况占10%,笔试40%,面试占50%计算总成绩,李武和周文两位同学的各项成绩如下表:(单位:分)
20. 某中学要从八年级学生中选报一名学生参加数学知识竞赛,需要从获奖情况、笔试、面试三个项目进行综合考查,按获奖情况占10%,笔试40%,面试占50%计算总成绩,李武和周文两位同学的各项成绩如下表:(单位:分)获奖情况
笔试
面试
周文
80
75
李武
70
80
88
(1)、计算李武同学的总成绩;(2)、若周文同学要在总成绩上超过李武同学,则他的面试成绩 应超过多少分?721. 在如图的网格中建立平面直角坐标系, 的顶点坐标分别为 , , , 是 与网格线的交点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示,并回答下列问题:
( 1 )在第一象限内画出平行四边形 ;
( 2 )画出点 关于 的对称点 ;
( 3 )过点 画出一条直线 ,使它平分平行四边形 的周长,请直接写出直线 的解析式;
( 4 )设过点 的直线 的解析式为 ,当直线 与平行四边形 有公共点,且直线 不与 轴平行时,请直接写出 的取值范围.
22. 如图1,已知 , , .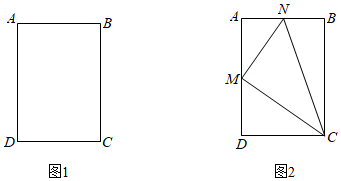 (1)、求证:四边形 为矩形(2)、如图2, 为 的中点, 为 的中点, .若 ,求 的长23. 某工厂安排300名工人生产 型、 型、 型三种产品共51件,生产这些产品每件所需工人数和产值如下表所示,且生产 型不少于14件.设 型、 型、 型三种产品分别为 件、 件和 件.
(1)、求证:四边形 为矩形(2)、如图2, 为 的中点, 为 的中点, .若 ,求 的长23. 某工厂安排300名工人生产 型、 型、 型三种产品共51件,生产这些产品每件所需工人数和产值如下表所示,且生产 型不少于14件.设 型、 型、 型三种产品分别为 件、 件和 件.产品
每件产品所需人数
每件产品产值
型
4
4.5万元
型
8
9万元
型
5
7.5万元
(1)、用含 的式子表示 和 ;(2)、若总产值 (万元),求 关于 的函数关系式;(3)、计划总产值 不低于360万元,工厂怎样安排三种产品的件数才能取得最优效益?24. 如图, 是正方形 边 上一个动点,线段 与 关于直线 对称,连接 并延长交直线 于点 ,连接 .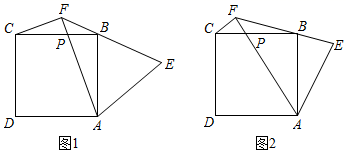 (1)、如图1, ,
(1)、如图1, ,①求 的大小;
②求证: ;
(2)、如图2,试猜想线段 与 之间的数量关系,并证明你的结论.