湖北省武汉市东西湖江岸区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-08-10 类型:期末考试
一、单选题
-
1. 二次根式 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、2. 下列各式中,运算正确的是( )A、 B、 C、 D、3. 以下列长度的线段为边,不能组成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 近日来,武汉市网红打卡点“武汉小锻仓”吸引众多市民前来拍照打卡,洪山区交警大队加强了该区域的交通管制,控制车辆速度,确保市民安全.某交警在该路口统计的某个时段,来往的 辆车行驶速度的分布如条形图所示这些车辆速度的众数是( )
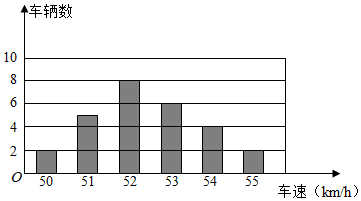 A、53 B、52 C、55 D、515. 将直线 向上平移4个单位长度后,所得的直线的解析式为( )A、 B、 C、 D、6. 下列性质中,矩形具有、正方形也具有、但是菱形却不具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、对角线长度相等 D、一组对角线平分一组对角7. 水龙头关闭不严会造成滴水,已知漏水量与漏水时间为一次函数关系,八( )班的同学进行了以下实验,在滴水的水龙头下放置一个能显示水量的容器,每10分钟记录一次容器中的水量,下表是一位同学的记录结果,老师发现有一组数据记录有较大偏差,它是( )
A、53 B、52 C、55 D、515. 将直线 向上平移4个单位长度后,所得的直线的解析式为( )A、 B、 C、 D、6. 下列性质中,矩形具有、正方形也具有、但是菱形却不具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、对角线长度相等 D、一组对角线平分一组对角7. 水龙头关闭不严会造成滴水,已知漏水量与漏水时间为一次函数关系,八( )班的同学进行了以下实验,在滴水的水龙头下放置一个能显示水量的容器,每10分钟记录一次容器中的水量,下表是一位同学的记录结果,老师发现有一组数据记录有较大偏差,它是( )时间
0
10
20
30
40
水量W(mL)
1
2.2
3.4
4.5
5.8
组别
1
2
3
4
5
A、第2组 B、第3组 C、第4组 D、第5组8. 如图 中, , , ,分别以三边为直径画半圆,则两月形图案的面积之和(阴影部分的面积)是( )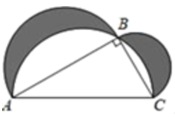 A、5π B、10π C、5 D、109. 如图,在矩形 中, 是 的中点,将 折叠后得到 ,点 在矩形内部,延长 交 于点 ,若 , ,则折痕 的长为( )
A、5π B、10π C、5 D、109. 如图,在矩形 中, 是 的中点,将 折叠后得到 ,点 在矩形内部,延长 交 于点 ,若 , ,则折痕 的长为( )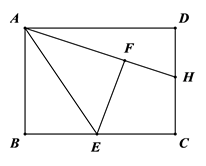 A、 B、 C、3 D、10. 已知函数 ( 为常数),当 时, 有最小值为5,则 的值为( )A、3或-1 B、3或4 C、-2或-1 D、-2或4
A、 B、 C、3 D、10. 已知函数 ( 为常数),当 时, 有最小值为5,则 的值为( )A、3或-1 B、3或4 C、-2或-1 D、-2或4二、填空题
-
11. 化简: = .12. 某学校欲招聘一名教师,对应聘者甲进行了笔试和面试,其笔试和面试的成绩分别为80分和90分,若按笔试成绩占30%,面试成绩占70%计算综合成绩,则甲的综合成绩为分.13. 平行四边形 两角线 、 交于点 , 为等边三角形,且 ,则 的长为.14. 如图,已知函数 和 ( 为常数,且 )的图象相交于点 ,则关于 的不等式 的解集为.
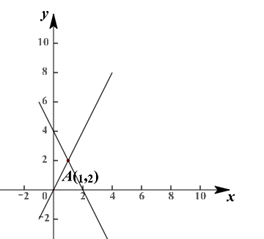 15. 如图,甲,乙两个工程队完成某项工程,首先是甲单独做了 天,然后乙队加入合做,完成剩下的全部工程.设工程总量为单位 ,工程进度满足如图所示的函数关系,设 甲的工作效率:乙的工作效率,则 的值为.
15. 如图,甲,乙两个工程队完成某项工程,首先是甲单独做了 天,然后乙队加入合做,完成剩下的全部工程.设工程总量为单位 ,工程进度满足如图所示的函数关系,设 甲的工作效率:乙的工作效率,则 的值为.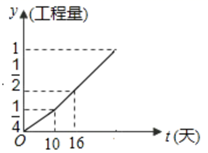 16. 如图,在 中, , , 平分 交 于点 . 为直线 上一动点.以 、 为邻边构造平行四边形 ,连接 ,若 .则 的最小值为.
16. 如图,在 中, , , 平分 交 于点 . 为直线 上一动点.以 、 为邻边构造平行四边形 ,连接 ,若 .则 的最小值为.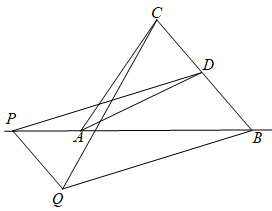
三、解答题
-
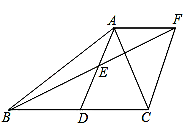
17. 计算:(1)、(2)、18. 如图,在 中, , 是中线, 是 的中点,过点 作 交 的延长线于 ,连接 .求证:四边形 是菱形.
 19. 武汉市教育局举办中小学生经典诵读活动,微发了同学们的读书热情.为了引导学生生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的数量最少的是5本,最多的是8本,并根据调查结果绘制了如图不完整的图表.
19. 武汉市教育局举办中小学生经典诵读活动,微发了同学们的读书热情.为了引导学生生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的数量最少的是5本,最多的是8本,并根据调查结果绘制了如图不完整的图表.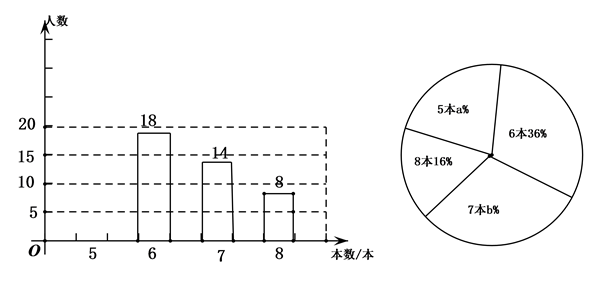 (1)、补全条形统计图,扇形统计图中的 ▲ .(2)、本次抽样调查中,中位数是 , 扇形统计图中课外阅读 本的扇形的圆心角大小为度;(3)、若该校八年级共有1200名学生,请估计该校八年级学生课外阅读至少7本的人数.20. 如图,在所给的正方形网格中,每个小正方形的边长均为1个单位.每个小正方形的顶点称为格点,如图格点 , , ,用无刻度的直尺作图.
(1)、补全条形统计图,扇形统计图中的 ▲ .(2)、本次抽样调查中,中位数是 , 扇形统计图中课外阅读 本的扇形的圆心角大小为度;(3)、若该校八年级共有1200名学生,请估计该校八年级学生课外阅读至少7本的人数.20. 如图,在所给的正方形网格中,每个小正方形的边长均为1个单位.每个小正方形的顶点称为格点,如图格点 , , ,用无刻度的直尺作图.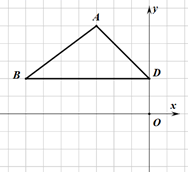 (1)、作平行四边形 ,则点 的坐标为 ▲ .(2)、作出 的中点 ,并直接写出直线 的解析式 ▲ ;(3)、在 轴上作出点 ,使得 .21. 如图,在平面直角坐标系 中,已知 , ,一次函数 的图象与直线 交于点 .
(1)、作平行四边形 ,则点 的坐标为 ▲ .(2)、作出 的中点 ,并直接写出直线 的解析式 ▲ ;(3)、在 轴上作出点 ,使得 .21. 如图,在平面直角坐标系 中,已知 , ,一次函数 的图象与直线 交于点 .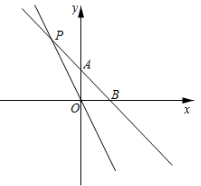 (1)、求 点的坐标;(2)、若 点是 轴上一点,且 的面积等于 ,求点 的坐标;(3)、若直线 与 的三边恰好有两个公共点.直接写出 的取值范围.22. 5月22日以来,大理市漾濞县连发多次地震,其中 、 两乡镇受灾非常严重. 、 两市获知 、 两乡镇分别需要救灾物资180吨和290吨后,决定调运物资支援 、 两乡镇.已知 市有救灾物资220吨, 市有救灾物资250吨,现将这些物资全部运往 、 两乡镇.已知从 市运往 、 两乡镇的费用分别是每吨22元和18元,从 市运往 、 两乡镇的费用分别是24元和25元,设 市运往 乡镇的救灾物资为 吨.(1)、请填写下表
(1)、求 点的坐标;(2)、若 点是 轴上一点,且 的面积等于 ,求点 的坐标;(3)、若直线 与 的三边恰好有两个公共点.直接写出 的取值范围.22. 5月22日以来,大理市漾濞县连发多次地震,其中 、 两乡镇受灾非常严重. 、 两市获知 、 两乡镇分别需要救灾物资180吨和290吨后,决定调运物资支援 、 两乡镇.已知 市有救灾物资220吨, 市有救灾物资250吨,现将这些物资全部运往 、 两乡镇.已知从 市运往 、 两乡镇的费用分别是每吨22元和18元,从 市运往 、 两乡镇的费用分别是24元和25元,设 市运往 乡镇的救灾物资为 吨.(1)、请填写下表合计吨
220
250
总计(吨)
180
290
470
(2)、设 、 两市运往 、 两乡镇的救灾物资总运费为 元,求总运费最小时的运输方案及最小运费;(3)、经过紧急抢修, 市运往 乡镇的路况得到改善,缩短了运输时间,每吨运费减少了 元 ,具体路线运费不变.若 、 两市运往 、 两乡镇的救灾物资总运费的最小值为9430元,求 的值.23. 正方形 中,点 在边 上,点 在边 上.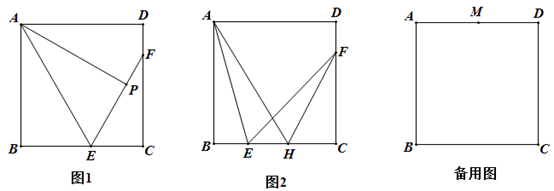 (1)、如图1,若 , 于点 ,当 时,求 的度数;(2)、如图2,若 ,点 在边 上,且在点 右侧,当 时,求证: .(3)、 为正方形 外一动点,且 , 为边 的中点,当 运动时,则 的最小值为.24. 如图1,直线 的解析式为 , 点坐标为 , 点关于直线 的对称点 点在直线 上.
(1)、如图1,若 , 于点 ,当 时,求 的度数;(2)、如图2,若 ,点 在边 上,且在点 右侧,当 时,求证: .(3)、 为正方形 外一动点,且 , 为边 的中点,当 运动时,则 的最小值为.24. 如图1,直线 的解析式为 , 点坐标为 , 点关于直线 的对称点 点在直线 上.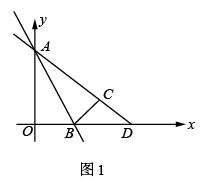
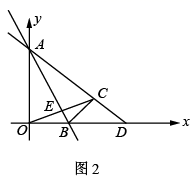
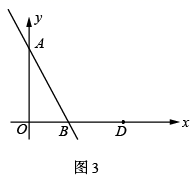 (1)、求直线 、 的解析式;(2)、如图2,若 交 于点 ,在线段 上是否存在一点 ,使 与 的面积相等,若存在求出 点坐标,若不存在,请说明理由;(3)、如图3,过点 的直线 .当它与直线 夹角等于 时,求出相应 的值.
(1)、求直线 、 的解析式;(2)、如图2,若 交 于点 ,在线段 上是否存在一点 ,使 与 的面积相等,若存在求出 点坐标,若不存在,请说明理由;(3)、如图3,过点 的直线 .当它与直线 夹角等于 时,求出相应 的值.