湖北省武汉市东湖高新区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-10 类型：期末考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{5 + x}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥0 B、x＞﹣5 C、x≠﹣5 D、x≥﹣5

查看试题解析
2. 下列各式中，运算正确的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 ${(\sqrt{3})}^{2} = \pm 3$ C、 $\sqrt{14} \times \sqrt{7} = 7 \sqrt{2}$ D、 $3 \sqrt{2} - \sqrt{2} = 3$

查看试题解析
3. 下列各组数据中，由线段a，b，c组成的三角形不是直角三角形的一组是（）

A、a＝6，b＝8，c＝10 B、a＝40，b＝50，c＝60 C、a＝ $\frac{5}{4}$ ，b＝1，c＝ $\frac{3}{4}$ D、a＝ $\sqrt{41}$ ，b＝4，c＝5

查看试题解析
4. 准备在甲，乙，丙，丁四人中选取成绩稳定的一名参加射击比赛，在相同条件下各人射击10次，已知他们的平均成绩相同，方差分别是S_甲²＝0.6，S_乙²＝1，S_丙²＝0.8，S_丁²＝2.3，则应该选择哪位运动员参赛（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 已知一次函数y＝2x﹣4，下列结论错误的是（）

A、图象与x轴的交点坐标（2，0） B、图象与y轴的交点坐标（0，﹣4） C、y随着x的增大而减小 D、当x＜2时，y＜0

查看试题解析
6. 菱形具有而一般平行四边形不具有的性质是（）

A、两组对边分别相等 B、两组对角分别相等 C、两条对角线互相平分 D、每一条对角线平分一组对角

查看试题解析
7. 若点A（x₁ ， ﹣1），B（x₂ ， ﹣2），C（x₃ ， 3）在一次函数y＝﹣2x+m（m是常数）的图象上，则x₁ ， x₂ ， x₃的大小关系是（）

A、x₁＞x₂＞x₃ B、x₂＞x₁＞x₃ C、x₁＞x₃＞x₂ D、x₃＞x₂＞x₁

查看试题解析
8. 水龙头关闭不严会造成滴水，为了调查滴水量与流水时间的关系，进行以下试验，并记录如表：

流水时间t/分钟

1

2

4

7

滴水量w/毫升

16

19

a

34

已知滴水量w与流水时间t之间为一次函数关系，以上记录的数据中a的值是（）

A、22 B、23 C、24 D、25

查看试题解析
9. 如图，正方形ABCD的边长为8，点E在CD边上，CE＝6，若点F在正方形的某一边上，满足CF＝BE，且CF与BE的交点为M，则CM的长度为（）

A、 $\frac{24}{5}$ B、7 C、5或 $\frac{24}{5}$ D、7或 $\frac{24}{5}$

查看试题解析
10. 已知a，b，c分别是Rt△ABC的三条边长，c为斜边长，∠C＝90°，我们把关于x的形如y＝ $\frac{a}{c} x + \frac{b}{c}$ 的一次函数称为“勾股一次函数”.若点P（﹣1， $\frac{\sqrt{2}}{2}$ ）在“勾股一次函数”的图象上，且Rt△ABC的面积是 $\frac{9}{2}$ ，则c的值是（）

A、6 B、12 C、2 $\sqrt{6}$ D、3 $\sqrt{2}$

查看试题解析

二、填空题

11. 化简 $\sqrt{\frac{3}{100}}$ 的结果是 .

查看试题解析
12. 现有一组数据：2，﹣1，0，4，5，7，这组数据的中位数为.

查看试题解析
13. 点（5，2）在直线y＝kx+b（k，b是常数，k≠0）上，则关于x的方程kx+b＝2的解x＝.

查看试题解析
14. 一个有进水管和出水管的容器，从某时刻开始4 min内只进水不出水，在随后的8 min内既进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y（1）与时间x(min)之间的关系如图所示，则每分钟的出水量为

查看试题解析
15. 已知一次函数y₁＝2kx+b（k，b是常数，k≠0），正比例函数y₂＝mx（m是常数，m≠0）.下列四个结论：
①若一次函数的图象与正比例函数的图象平行，则k＝ $\frac{m}{2}$ ；

②若kb＜0，则一次函数的图象经过第一、二、四象限；

③将一次函数图象向右平移2个单位长度，则平移后的图象对应的函数解析式为y＝2kx﹣4k+b；

④若b＝2﹣k，当x＞ $\frac{1}{2}$ 时，y₁总是小于y₂ ，则m≥4.

其中正确的结论是（填写序号）.

查看试题解析
16. 课堂上小强进行如下实践操作：
第一步，将一张矩形纸片利用图1的方法折出一个正方形，然后把纸片展平；

第二步，如图2，把这个正方形折成两个全等的矩形，然后把纸片展平；

第三步，如图3，折出内侧矩形AFBC的对角线AB，并把AB沿AQ对折到AD处；

第四步，如图4，展平纸片，按照所得的点D折出DE，得矩形BCDE.

则 $\frac{B E}{D E}$ ＝.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{80} - \sqrt{20} + \sqrt{5}$ ；

(2)、 $(\sqrt{5} + \sqrt{3}) (\sqrt{5} - \sqrt{3})$ .

查看试题解析
18. 如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD．
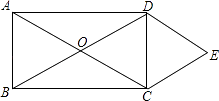
求证：四边形OCED是菱形．

查看试题解析

19. 在“世界读书日”来临之际，某校为了解学生的课外阅读情况，从全校随机抽取了部分学生，调查了他们平均每周的课外阅读时间t（单位：h）.整理所得数据绘制成不完整的统计图表.

平均每周的课外阅读时间频数分布表

组别	平均每周的课外阅读时间t/h	人数
A	t＜6	16
B	6≤t＜8	a
C	8≤t＜10	b
D	t≥10	8

根据以上图表信息，解答下列问题：

(1)、这次抽样调查的样本容量是， a＝；

(2)、B组所在扇形的圆心角的大小是；

(3)、该校共1600名学生，请你估计该校学生平均每周的课外阅读时间不少于8h的人数.

查看试题解析

20. 已知函数y₁＝（m+1）x﹣m²+1（m是常数）.

(1)、m为何值时，y₁随x的增大而减小；

(2)、m满足什么条件时，该函数是正比例函数？

(3)、若该函数的图象与另一个函数y₂＝x+n（n是常数）的图象相交于点（m，3），求这两个函数的图象与y轴围成的三角形的面积.

查看试题解析
21. 如图是由边长为1的小正方形构成6×6的网格，每个小正方形的顶点叫做格点.四边形ABCD的顶点都是格点，点E是边AD与网格线的交点.仅用无刻度尺的直尺在给定网格中画图，画图过程用虚线表示，画图结果用实线表示，按步骤完成下列问题：

（ 1 ）直接写出四边形ABCD的形状；

（ 2 ）在BC边上画点F，连接EF，使得四边形AEFB的面积为5；

（ 3 ）画出点E绕着B点逆时针旋转90°的对应点G；

（ 4 ）在CD边（端点除外）上画点H，连接EH，使得EH＝AE+CH.

查看试题解析
22. 某公司分别在A，B两城生产同种产品，共100件.A生产的产品总成本y（万元）与产品数量x（件）之间具有函数关系y＝kx+b.当x＝10时，y＝130；当x＝20时，y＝230.B城生产的产品每件成本为60万元，若B城生产的产品数量至少比A城生产的产品数量多40件.

(1)、求k，b的值；

(2)、当A，B两城生产这批产品的总成本的和最少时，求A，B两城各生产多少件？

(3)、从A城把该产品运往C，D两地的费用分别为m万元/件和3万元/件；从B城把该产品运往C，D两地的费用分别为1万元/件和2万元/件.C地需要90件，D地需要10件，在（2）的条件下，直接写出A，B两城总运费的和的最小值（用含有m的式子表示）.

查看试题解析
23. 正方形ABCD中，点E为对角线BD上任意一点（不与B，D重合），连接AE，过点E作EF⊥AE，交线段BC于点F.

(1)、如图1，求证：AE＝EF；

(2)、如图2，EG⊥BD，交线段CD于点G，EF与BG相交于点H，若点H是BG的中点，求证：AE＝ $\sqrt{2}$ EH；

(3)、若 $\frac{D E}{D B} = \frac{1}{3}$ ，直接写出 $\frac{B F}{F C}$ 的值.

查看试题解析
24. 在平面直角坐标系中，直线y＝kx+8k（k是常数，k≠0）与坐标轴分别交于点A，点B，且点B的坐标为（0，6）.

(1)、求点A的坐标；

(2)、如图1，将直线AB绕点B逆时针旋转45°交x轴于点C，求直线BC的解析式；

(3)、在（2）的条件下，直线BC上有一点M，坐标平面内有一点P，若以A、B、M、P为顶点的四边形是菱形，请直接写出点P的坐标.

查看试题解析

流水时间t/分钟	1	2	4	7
滴水量w/毫升	16	19	a	34