湖北省随州市广水市2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-10 类型：期末考试

进入出卷网下载

一、单选题

1. 下列根式是最简二次根式的是（）

A、 $\sqrt{\frac{1}{5}}$ B、 $\sqrt{0.5}$ C、 $\sqrt{5}$ D、 $\sqrt{28}$

查看试题解析
2. 已知△ABC中，a、b、c分别是∠A、∠B、∠C的对边，下列条件中不能判断△ABC是直角三角形的是（）

A、∠A：∠B：∠C＝3：4：5 B、∠C＝∠A﹣∠B C、a²+b²＝c² D、a：b：c＝6：8：10

查看试题解析
3. 如下图，直线l上有三个正方形a，b，c，若a，c的面积分别为7，18，则b的面积为（）

A、9 B、67 C、25 D、126

查看试题解析
4. 已知，如图，长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（）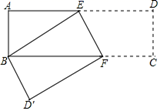

A、6cm² B、8 cm² C、10 cm² D、12 cm²

查看试题解析
5. 如图，四边形 $A B C D$ 的两条对角线相交于点 $O$ ，且互相平分.添加下列条件，仍不能判定四边形 $A B C D$ 为菱形的是（）

A、 $A C ⊥ B D$ B、 $A B = A D$ C、 $A C = B D$ D、 $∠ A B D = ∠ C B D$

查看试题解析
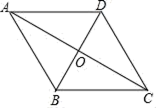6. 如下图，平行四边形ABCD的对角线AC与BD相交于点O，AB⊥AC，若AB＝4，AC＝6，则BD的长是（）

A、10 B、9 C、8 D、11

查看试题解析
7. 下列图象中不可能是一次函数y=mx-（m-3）的图象的是（）

A、 B、 C、 D、

查看试题解析
8. 某手表厂抽查了10只手表的日走时误差，数据如下表所示：则这10只手表的平均日走时误差（单位：秒）是（）

日走时误差（秒）

0

1

2

3

只数（只）

3

4

2

1

A、0 B、0.6 C、0.8 D、1.1

查看试题解析
9. 如图，点A，B，C在一次函数y= -2x+m的图象上，它们的横坐标依次为-1，1，2，分别过这些点作x轴与y轴的垂线，则图中的阴影部分的面积之和是（）

A、1 B、3 C、3（m-1） D、 $\frac{3}{2} (m - 2)$

查看试题解析
10. 一条公路旁依次有A，B，C三个村庄，甲乙两人骑自行车分别从A村，B村同时出发前往C村，甲乙之间的距离S（km）与骑行时间t（h）之间的函数关系如图所示，下列结论：① A，B两村相距10km；② 出发1.25h后两人相遇；③ 甲每小时比乙多骑行8km；④ 相遇后，乙又骑行了15min或65min时两人相距2km；⑤ 两人最远相距6km.其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 化简 $\sqrt{1 \frac{7}{9}}$ =.

查看试题解析
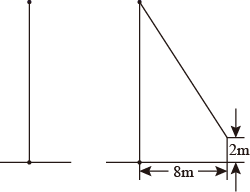
12. 函数y= $\frac{\sqrt{x + 2}}{x}$ 中，自变量x的取值范围是．

查看试题解析
13. 如图，小亮将升旗的绳子拉到旗杆底端，绳子刚好接触到地面，然后将绳子末端拉到距离旗杆8m处，发现此时绳子末端离地面2m，则旗杆的高度（滑轮上方的部分忽略不计）为m.

查看试题解析
14. 如图，在Rt△ABC中，∠ACB＝90°，D，E分别是AB，AC的中点，连接CD，过E作EF∥DC交BC的延长线于F，若四边形CDEF的周长是10cm，AC的长为4cm，则△ABC的周长是cm.

查看试题解析
15. 已知菱形ABCD的边长为6， $∠ A = 60 °$ ，如果点P是菱形内一点，且 $P B = P D = 2 \sqrt{3}$ ，那么 $A P$ 的长为.

查看试题解析
16. 如图，正方形ABCD中，AB=6，点E在边CD上，且CD＝3DE，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG，CF，完成下列填空：①∠GAE的度数为；② $S_{△ F G C} ＝$ .

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{27} + \frac{\sqrt{18}}{3} - \sqrt{0.5} - \frac{6}{\sqrt{3}}$ ；

(2)、 $(\sqrt{5} - \sqrt{3}) \times (\sqrt{5} + \sqrt{3}) - {(\sqrt{2} + \sqrt{6})}^{2}$ ；

查看试题解析
18. 先化简，再计算： $\frac{x^{2} - x - 2}{x} \cdot \frac{1}{x - 2} - \frac{2 x + 2}{x^{2} + x}$ ，其中x＝ $\sqrt{2} + 1$ ．

查看试题解析
19. 如图，点D，E，F分别是△ABC各边中点.

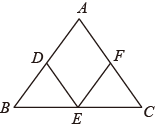(1)、求证：四边形ADEF是平行四边形；

(2)、若AB=AC=10，BC=12，求四边形ADEF的周长和面积.

查看试题解析
20. 如图，在 $▱$ ABCD中，AC⊥AB，AC与BD相交于点O，将△ABC沿对角线AC翻转180°，得到△AB'C.

(1)、求证：以A，C，D，B' 为顶点的四边形是矩形；

(2)、若四边形ABCD的面积为12平方厘米，求翻转后重叠部分的面积，即△ACE的面积.

查看试题解析
21. 为了解学生参加户外活动的情况，和谐中学对学生每天参加户外活动的时间进行抽样调查，并将调查结果绘制成如图两幅不完整的统计图，根据图示，请回答下列问题：

(1)、被抽样调查的学生有 ▲ 人，并补全条形统计图；

(2)、每天户外活动时间的中位数是(小时)；

(3)、该校共有2000名学生，请估计该校每天户外活动时间超过1小时的学生有多少人？

查看试题解析
22. 某公司有A产品40件，B产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完.两商店销售这两种产品每件的利润 (元) 如下表所示：

A产品的利润/元

B产品的利润/元

甲店

200

170

乙店

160

150

(1)、设分配给甲店A产品x件，这家公司卖出这100件产品的总利润为W (元)，求W关于x的函数关系式，并求出x的取值范围；

(2)、若要求总利润不低于17560元；有多少种不同的分配方案? 并将各种方案设计出来；

(3)、为了促销，公司决定仅对甲店A产品让利销售，每件让利a元，但让利后A产品的每件利润仍高于甲店B产品的每件利润.甲店的B产品以及乙店的A，B产品的每件利润不变，问该公司又如何设计分配方案，使总利润达到最大?

查看试题解析
23. 阅读材料：基本不等式 $\sqrt{a b} \leq \frac{a + b}{2} (a > 0 ， b > 0)$ 当且仅当a=b时，等号成立，其中我们把 $\frac{a + b}{2}$ 叫做正数a，b的算术平均数， $\sqrt{a b}$ 叫做正数a，b的几何平均数，它是解决最大（小）值问题的有力工具，例如：在x＞0的条件下，当x为何值时， $x + \frac{1}{x}$ 有最小值？最小值是多少？
解：∵x＞0， $\frac{1}{x} > 0$ ，∴ $\frac{x + \frac{1}{x}}{2}$ ≥2 $\sqrt{x \cdot \frac{1}{x}}$ ，∴ $x + \frac{1}{x} \geq 2$ ，当且仅当 $x ＝ \frac{1}{x}$ 时，即x=1时，有 $x + \frac{1}{x}$ 有最小值为2.

请根据阅读材料解答下列问题：

(1)、填空：当 $x$ >0时，设 $y = x + \frac{4}{x}$ ，则当且仅当 $x$ =时，y有最值为；

(2)、若 $x$ ＞0，函数 $y = 2 x + \frac{1}{x}$ ，当x为何值时，函数有最值？并求出其最值；

(3)、在Rt△ABC中，∠C＝90°，若△ABC的面积等于8，求△ABC周长的最小值.

查看试题解析
24. 如图，在平面直角坐标系中，直线 $y = - \frac{\sqrt{3}}{2} x - 2 \sqrt{3}$ 与x轴，y轴分别交于点A，C，经过点C的直线与x轴交于点B（2，0）.

(1)、求直线BC的解析式；

(2)、点P是线段AC上一动点，若直线BP把△ABC的面积分成1：2的两部分，请求点P的坐标；

(3)、若点P是直线AC上一动点，点E是坐标轴上一动点，则是否存在动点P使以点B，C，P，E为顶点的四边形是以BC为一边的平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由.

查看试题解析

	A产品的利润/元	B产品的利润/元
甲店	200	170
乙店	160	150

日走时误差（秒）	0	1	2	3
只数（只）	3	4	2	1