湖北省黄石市西塞山区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-10 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，不能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{8}$ C、 $\sqrt{18}$ D、 $\sqrt{12}$

查看试题解析
2. 如图，在▱ABCD中，DE平分∠ADC，AD=8，BE=3，则▱ABCD的周长是（　　）

A、16 B、14 C、26 D、24

查看试题解析
3. 某次文艺演中若干名评委对八（1）班节目给出评分.在计算中去掉一个最高分和最低分.这种操作，对数据的下列统计一定不会影响的是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
4. 如图，在 $Δ A B C$ 中，AD⊥BC于 D， AB=3，DB=2，DC=1，则AC等于（）

A、6 B、 $\sqrt{6}$ C、 $\sqrt{5}$ D、4

查看试题解析
5. 一次函数 $y = - 3 x + m$ 的图象经过点 $P (- 2 ， 3)$ ，若 $Q (q ， 1)$ 也在此函数图象上，则 $q$ 的值为（）

A、 $- \frac{4}{3}$ B、 $- \frac{3}{4}$ C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
6. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 相交于点 $O$ ， $A E$ 垂直平分 $B O$ ，若 $A E = 2 \sqrt{3}$ cm，则 $O D =$ （）

A、 $2 c m$ B、3cm C、 $4 c m$ D、 $6 c m$

查看试题解析
7. 如图，直线 $y = - x + m$ 与 $y = n x + 4 n (n \neq 0)$ 的交点的横坐标为 $- 2$ ，则关于 $x$ 的不等式 $- x + m > n x + 4 n > 0$ 的整数解为（）.

A、-1 B、-5 C、-4 D、-3

查看试题解析
8. 已知一次函数y＝(m－4)x＋2m＋1的图象不经过第三象限，则m的取值范围是（）

A、m＜4 B、 $- \frac{1}{2}$ ≤m＜4 C、 $- \frac{1}{2}$ ≤m≤4 D、m≤ $- \frac{1}{2}$

查看试题解析
9. 如图，在△ABC中，∠C=90°，E是CA延长线上一点，F是CB上一点，AE=12，BF=8，点P，Q，D分别是AF，BE，AB的中点，则PQ的长为（）

A、2 $\sqrt{13}$ B、4 C、6 D、3 $\sqrt{5}$

查看试题解析
10. 如图，在正方形ABCD中，E是对角线BD上一点，且满足 $B E$ =AD，连接CE并延长交AD于点F，连接AE，过点B作 $B G ⊥ A E$ 于点G，延长BG交AD于点H.在下列结论中：① $A H = D F$ ；② $∠ A E F = 45 °$ ；③ $S_{四边形 E F H G} = S_{△ D E F} + S_{△ A G H}$ . 其中不正确的结论有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

11. 计算 $\sqrt{54} - 6 \sqrt{\frac{2}{3}}$ 的结果为.

查看试题解析

12. 表中记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差，根据表中数据，要从中选择一名成定的运动员参加比赛，应选择.

	甲	乙	丙	丁
平均数（环）	9.14	9.15	9.14	9.15
方差	6.6	6.8	6.7	6.6

查看试题解析

13. 函数 $y = \frac{1}{1 - x} + \sqrt{x + 2}$ 中，自变量x的取值范围是．

查看试题解析
14. 若直角三角形的两边长分别为1和2，则斜边上的中线长为.

查看试题解析
15. 如图，已知∠ADC=90°，AD=8m，CD=6m，BC=24m，AB=26m，则图中阴影部分的面积为；

查看试题解析
16. 已知直线 $y = k x - 2$ 上有一点 B(1，b)，点 B 到原点的距离为 $\sqrt{10}$ ，则该直线与两坐标轴围成的三角形的面积为.

查看试题解析
17. 点P是菱形ABCD的对角线AC上的一个动点，已知AB=1，∠ADC=120°，点M，N分别是AB，BC边上的中点，则△MPN的周长最小值是.

查看试题解析
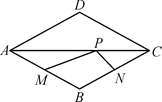18.
如图，在平面直角坐标系中，将△ABO绕点B顺时针旋转到△A₁BO₁的位置，使点A的对应点A₁落在直线y= $\frac{\sqrt{3}}{3}$ x上，再将△A₁BO₁绕点A₁顺时针旋转到△A₁B₁O₂的位置，使点O₁的对应点O₂落在直线y= $\frac{\sqrt{3}}{3}$ x上，依次进行下去…，若点A的坐标是（0，1），点B的坐标是（ $\sqrt{3}$ ，1），则点A₈的横坐标是．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{18} + \sqrt{12} - \sqrt{8} - \sqrt{27}$

(2)、 $(1 - \sqrt{5}) (\sqrt{5} + 1) + {(\sqrt{5} - 1)}^{2}$

查看试题解析
20. 如图，直线 $y = - \frac{1}{2} x + b$ 与 $x$ 轴， $y$ 轴分别交于点 $A$ ，点 $B$ ，与函数 $y = k x$ 的图象交于点 $M (1 ， 2)$ .

(1)、求 $k$ ， $b$ 的值；

(2)、点C在线段 $M A$ 上，过点 $C$ 作 $x$ 轴的垂线，交函数 $y = k x$ 的图象于点 $D$ ，若 $2 C D = O B$ ，求点 $C$ 的坐标.

查看试题解析
21. 如图，已知点E、F分别是平行四边形ABCD的边BC、AD上的点，且BE=DF

(1)、求证：四边形AECF是平行四边形；

(2)、若四边形AECF是菱形，且BC=10，∠BAC=90°，求BE的长.

查看试题解析
22. 为创建足球特色学校，营造足球文化氛围，某学校随机抽取部分八年级学生足球运球的测试成绩作为一个样本，按A，B，C，D四个等级进行统计，制成了如下不完整的统计图.（说明：A级：8分—10分，B级：7分—7.9分，C级：6分—6.9分，D级：1分—5.9分）根据所给信息，解答以下问题：

(1)、样本容量为 ▲ ，C对应的扇形的圆心角是 ▲ 度，补全条形统计图；

(2)、所抽取学生的足球运球测试成绩的中位数会落在等级；

(3)、该校八年级有300名学生，请估计足球运球测试成绩达到 $A$ 级的学生有多少人？

查看试题解析
23. 某服装店准备购进甲、乙两种服装出售，甲种每件售价120元，乙种每件售价90元.每件甲服装的进价比乙服装的进价贵20元，购进3件甲服装的费用和购进4件乙服装的费用相等，现计划购进两种服装共100件，其中甲种服装不少于65件.

(1)、甲种服装进价为元/件，乙种服装进价为元/件；

(2)、若购进这100件服装的费用不得超过7500元.
①求甲种服装最多购进多少件？

②该服装店对甲种服装每件降价 $a (0 < a < 20)$ 元，乙种服装价格不变，如果这100件服装都可售完，那么该服装店如何进货才能获得最大利润？

查看试题解析
24. 如图，在正方形 ABCD 中，点 E 是对角线 BD 上一动点，AE 的延长线交 CD 于点 F，交 BC 的延长线于点 G，M 是 FG 的中点.

(1)、求证： ∠DAE=∠DCE；

(2)、判断线段 CE 与 CM 的位置关系，并证明你的结论；

(3)、当 $A D = \sqrt{3} + 1$ ，并且 $Δ C E G$ 恰好是等腰三角形时，求 DE 的长.

查看试题解析
25. 如图1，在平面直角坐标系中，直线 $y = - \frac{1}{2} x + 2$ 与坐标轴交于 $A$ ， $B$ 两点，以 $A B$ 为斜边在第一象限内作等腰直角三角形 $A B C$ .点 $C$ 为直角顶点，连接 $O C$ .

(1)、 $A$ 点坐标为， $B$ 点坐标为.

(2)、请你过点 $C$ 作 $C E ⊥ y$ 轴于 $E$ 点，试探究并证明 $O B + O A$ 与 $C E$ 的数量关系.

(3)、如图2，将线段 $A B$ 绕点 $B$ 沿顺时针方向旋转至 $B D$ ，且 $O D ⊥ A D$ ，延长 $D O$ 交直线 $y = x + 5$ 于点 $P$ ，求点 $P$ 的坐标.

查看试题解析