湖北省黄石市黄石港区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-08-10 类型:期末考试
一、单选题
-
1. 下列根式中不是最简二次根式的是( )A、 B、 C、 D、2. 下列各组数中,能构成直角三角形的三边的长度是( )A、3,5,7 B、5,22,23 C、 , , D、0.3,0.4,0.53. 正方形具有而矩形没有的性质是( )A、对角线互相平分 B、每条对角线平分一组对角 C、对角线相等 D、对边相等4. 一次函数y=2x-2的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 在 ABCD中,AC,BD是对角线,如果添加一个条件,即可推出 ABCD是矩形,那么这个条件是( )A、AB=BC B、AC=BD C、AC⊥BD D、AB⊥BD6. 一次函数 ,若 ,则它的图象必经过点( )A、 B、 C、 D、7. 比较 的大小,正确的是( )A、 B、 C、 D、8. 某人驾车从 地走高速公路前往 地,中途在服务区休息了一段时间.出发时油箱中存油40升,到 地后发现油箱中还剩油4升,则从 地出发到达 地的过程中,油箱中所剩燃油 升)与时间 (小时)之间的函数图象大致是( )A、
 B、
B、 C、
C、 D、
D、 9. 某校八年级甲、乙两班举行电脑汉字输入速度比赛,两个班参加比赛的学生每分钟输入汉字的个数经统计和计算后结果如下表:
9. 某校八年级甲、乙两班举行电脑汉字输入速度比赛,两个班参加比赛的学生每分钟输入汉字的个数经统计和计算后结果如下表:班级
参加人数
中位数
方差
平均字数
甲
55
149
191
135
乙
55
151
110
135
有一位同学根据上表得出如下结论:①甲、乙两班学生的平均水平相同;②乙班优秀的人数比甲班优秀的人数多(每分钟输入汉字达150个以上为优秀)﹔③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大.上述结论正确的是( )
A、①②③ B、①② C、①③ D、②③10. 如图,等边 与正方形 重叠,其中D,E两点分别在 , 上,且 ,若 , ,则 的面积为( )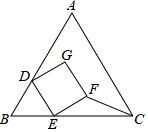 A、1 B、 C、2 D、
A、1 B、 C、2 D、二、填空题
-
11. 二次根式 中,字母 的取值范围是 .12. 已知一次函数y=2x+1,则它的图象与坐标轴围成的三角形面积是 .
13. 在一次函数 中,当 时, 的最小值为.14. 如图,已知∠B=∠C=∠D=∠E=90°,且AB=CD=3,BC=4,DE=EF=2,则AF的长是. 15. 如图,已知函数 和 的图象交点为 ,则不等式 的解集为.
15. 如图,已知函数 和 的图象交点为 ,则不等式 的解集为.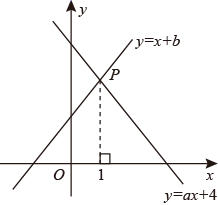 16. 正方形 …按如图所示的方式放置,点 …和点 …分别在直线 和 轴上,已知点 ,点 的坐标是.
16. 正方形 …按如图所示的方式放置,点 …和点 …分别在直线 和 轴上,已知点 ,点 的坐标是.
三、解答题
-
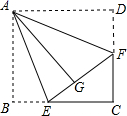
17. 计算:(1)、 ;(2)、 .18. 已知y与 成正比例,且 时, .(1)、求y与x之间的函数关系式;(2)、设点( ,-2)在(1)中函数的图象上,求 的值.19. 如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,求EF的长.
 20. 在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发 (h)时,汽车与甲地的距离为 (km), 与 的函数关系如图所示.
20. 在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发 (h)时,汽车与甲地的距离为 (km), 与 的函数关系如图所示.
根据图象信息,解答下列问题:
(1)、这辆汽车的往、返速度是否相同?请说明理由;(2)、求返程中 与 之间的函数表达式;(3)、求这辆汽车从甲地出发4h时与甲地的距离.21. 某学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为区级先进班集体,下表是这三个班的五项素质考评得分表:五项素质考评得分表(单位:分)
班级
行为规范
学习成绩
校运动会
艺术获奖
劳动卫生
甲班
10
10
6
10
7
乙班
10
8
8
9
8
丙班
9
10
9
6
9
根据统计表中的信息解答下列问题:
(1)、请你补全五项成绩考评分析表中的数据:五项成绩考评分析表
班级
平均分
中位数
众数
甲班
8.6
10
乙班
8.6
8
丙班
9
9
(2)、如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按照 的比确定,学生处的李老师根据这个平均成绩,绘制一幅不完整的条形统计图,请将这个统计图补充完整,依照这个成绩,应推荐哪个班为区级先进班集体? 22. 已知: 是正方形 对角线 上一点, ,垂足分别为 .
22. 已知: 是正方形 对角线 上一点, ,垂足分别为 .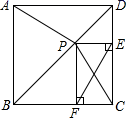 (1)、求证: ;(2)、若 ,求 的长.23. 为迎接“国家级文明卫牛城市”检查,我市环卫局准备购买 两种型号的垃圾箱。通过市场调研发现:购买1个 型垃圾箱和2个 型垃圾箱需340元;购买3个 型垃圾箱和2个 型垃圾箱共需540元.(1)、求每 个型垃圾箱和 型垃圾箱各多少元?(2)、该市现需要购买 两种型号的垃圾箱20个,其中购买 型垃圾箱不超过16个.
(1)、求证: ;(2)、若 ,求 的长.23. 为迎接“国家级文明卫牛城市”检查,我市环卫局准备购买 两种型号的垃圾箱。通过市场调研发现:购买1个 型垃圾箱和2个 型垃圾箱需340元;购买3个 型垃圾箱和2个 型垃圾箱共需540元.(1)、求每 个型垃圾箱和 型垃圾箱各多少元?(2)、该市现需要购买 两种型号的垃圾箱20个,其中购买 型垃圾箱不超过16个.①求购买垃圾箱的总花费 (元)与 型垃圾箱 (个)之间的函数关系式;
②当购买 型垃圾箱个数多少时总费用最小,最小费用是多少?
24. 如图,在Rt ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动.同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF. (1)、求证:AE=DF;(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)、当t为何值时, DEF为直角三角形?请说明理由.25. 在平面直角坐标系 中,一次函数 为常数,且 )的图象经过点 .
(1)、求证:AE=DF;(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)、当t为何值时, DEF为直角三角形?请说明理由.25. 在平面直角坐标系 中,一次函数 为常数,且 )的图象经过点 . (1)、求一次函数的解析式;(2)、无论 取何值,一次函数 为常数,且 )的图象必经过一个固定的点 .
(1)、求一次函数的解析式;(2)、无论 取何值,一次函数 为常数,且 )的图象必经过一个固定的点 .①求点 的坐标;
②在 轴上是否存在一点 使得 是等腰三角形?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.