湘教版数学七年级上册同步训练《4.1 几何图形》
试卷更新日期:2021-08-10 类型:同步测试
一、单选题
-
1. 下列几何体中,圆柱体是( )A、
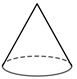 B、
B、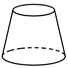 C、
C、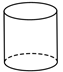 D、
D、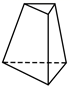 2. 下列图形中,可能是圆锥侧面展开图的是( )
2. 下列图形中,可能是圆锥侧面展开图的是( ) A、
A、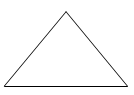 B、
B、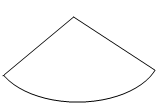 C、
C、 D、
D、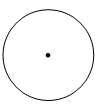 3. 把图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )
3. 把图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )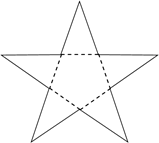 A、五棱锥 B、五棱柱 C、六棱锥 D、六棱柱4. 某几何体的展开图如图所示,该几何体是( )
A、五棱锥 B、五棱柱 C、六棱锥 D、六棱柱4. 某几何体的展开图如图所示,该几何体是( )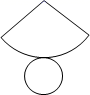 A、
A、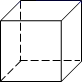 B、
B、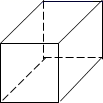 C、
C、 D、
D、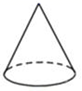 5. 如图是一个正方体的展开图,把展开图折叠成小正方体后,和“建”字所在面相对的面上的字是( )
5. 如图是一个正方体的展开图,把展开图折叠成小正方体后,和“建”字所在面相对的面上的字是( ) A、跟 B、百 C、走 D、年6. 一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )
A、跟 B、百 C、走 D、年6. 一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )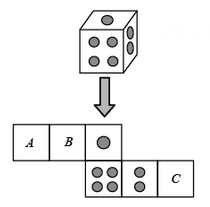 A、 代表
A、 代表 B、 代表
B、 代表  C、 代表
C、 代表  D、 代表
D、 代表  7. 下列图形中,不是正方体表面展开图的是( )A、
7. 下列图形中,不是正方体表面展开图的是( )A、 B、
B、 C、
C、 D、
D、 8. 已知图1的小正方形和图2中所有的小正方形都全等,将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置,放置后所组成的图形是不能围成一个正方体的.那么安放的位置是( )
8. 已知图1的小正方形和图2中所有的小正方形都全等,将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置,放置后所组成的图形是不能围成一个正方体的.那么安放的位置是( ) A、① B、② C、③ D、④
A、① B、② C、③ D、④二、填空题
-
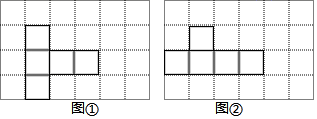
9. 如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有1个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有种拼接方法.
 10. 如图,在长方体 ABCD -EFGH中,与棱CD异面的棱有条.
10. 如图,在长方体 ABCD -EFGH中,与棱CD异面的棱有条. 11. 如图是一个正方体纸盒的展开图,正方体的各面标有数1,2,3, ,A,B,相对面上两个数和相等,则 .
11. 如图是一个正方体纸盒的展开图,正方体的各面标有数1,2,3, ,A,B,相对面上两个数和相等,则 .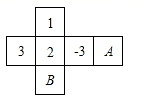 12. 如图是一个正方体的表面展开图,则折成正方体后,与点 重合的点是点.
12. 如图是一个正方体的表面展开图,则折成正方体后,与点 重合的点是点.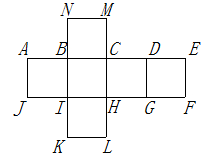 13. 一个正方体的平面展开图如图,已知正方体相对两个面上的数之和为零,则 .
13. 一个正方体的平面展开图如图,已知正方体相对两个面上的数之和为零,则 .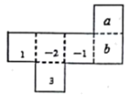 14. 有一个正六面体骰子,放在桌面上,将骰子沿如图所示的方式滚动,每滚动90°算一次,则滚动第2021次后,骰子朝下一面的点数是.
14. 有一个正六面体骰子,放在桌面上,将骰子沿如图所示的方式滚动,每滚动90°算一次,则滚动第2021次后,骰子朝下一面的点数是. 15. 十八世纪数学家欧拉证明了简单多面体中顶点数( ),面数( ),棱数( )之间存在一个有趣的数量关系: ,这就是著名的欧拉定理.某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形拼接而成,且有24个顶点,每个顶点都有3条棱,设该多面体外表面三角形个数是 个,八边形的个数是 ,则x+y= .16. 如图,直角三角形绕直线L旋转一周,得到的立体图形是.
15. 十八世纪数学家欧拉证明了简单多面体中顶点数( ),面数( ),棱数( )之间存在一个有趣的数量关系: ,这就是著名的欧拉定理.某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形拼接而成,且有24个顶点,每个顶点都有3条棱,设该多面体外表面三角形个数是 个,八边形的个数是 ,则x+y= .16. 如图,直角三角形绕直线L旋转一周,得到的立体图形是.
三、解答题
-
17. 如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
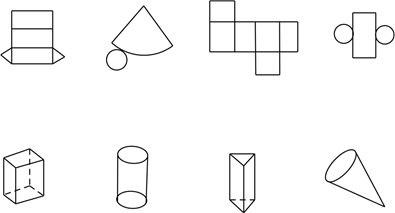 18. 正方体是由六个平面图形围成的立体图形.设想沿着正方体的一些棱将它剪开,就可以把正方体剪成一个平面图形.但同一个正方体,按不同的方式展开所得的平面展开图悬不一样的,下面的图形是由6个大小一样的正方彤,拼接而成的,请问这些图形中哪些可以折成正方体?
18. 正方体是由六个平面图形围成的立体图形.设想沿着正方体的一些棱将它剪开,就可以把正方体剪成一个平面图形.但同一个正方体,按不同的方式展开所得的平面展开图悬不一样的,下面的图形是由6个大小一样的正方彤,拼接而成的,请问这些图形中哪些可以折成正方体?