第十二章 全等三角形 单元测试----初中数学人教版八年级上册
试卷更新日期:2021-08-09 类型:单元试卷
一、单选题
-
1. 下列说法不正确的是( ).A、两边和它们的夹角分别相等的两个三角形全等 B、两角分别相等且其中一组等角的对边相等的两个三角形全等 C、底边和顶角分别相等的两个等腰三角形全等 D、两边和其中一边的对角分别相等的两个三角形全等2. 如图,OC为∠AOB的平分线,CM⊥OB, COM的面积为9,OM=6,则点C到射线OA的距离为( )
 A、9 B、6 C、3 D、4.53. 如图,在 中, , 是 的角平分线,若 ,则点 到 边的距离为( )
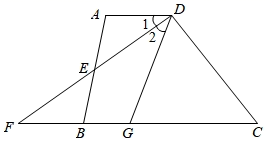
A、9 B、6 C、3 D、4.53. 如图,在 中, , 是 的角平分线,若 ,则点 到 边的距离为( )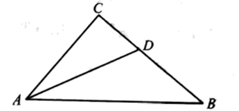 A、1 B、 C、2 D、34. 如图, 和 中,点 , , , 在同一直线上,在① ,② ,③ ,④ ,⑤ 五个条件中,能使 与 全等的条件的序号是( )
A、1 B、 C、2 D、34. 如图, 和 中,点 , , , 在同一直线上,在① ,② ,③ ,④ ,⑤ 五个条件中,能使 与 全等的条件的序号是( ) A、①②③ B、①②④ C、①③④ D、③④⑤5. 如图,若 ,则下列结论中不一定成立的是( )
A、①②③ B、①②④ C、①③④ D、③④⑤5. 如图,若 ,则下列结论中不一定成立的是( ) A、 B、 C、 D、6. 如图,E是线段AB的中点,∠AEC=∠DEB , 再添加一个条件,使得△AED≌△BEC , 所添加的条件不正确的是( )
A、 B、 C、 D、6. 如图,E是线段AB的中点,∠AEC=∠DEB , 再添加一个条件,使得△AED≌△BEC , 所添加的条件不正确的是( ) A、AD=BC B、DE=CE C、∠A=∠B D、∠C=∠D7. 一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是( )
A、AD=BC B、DE=CE C、∠A=∠B D、∠C=∠D7. 一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是( ) A、① B、② C、③ D、④8. 如图,已知 是平角, 平分 ,在平面上画射线 ,使 和 互余,若 ,则 的度数为( )
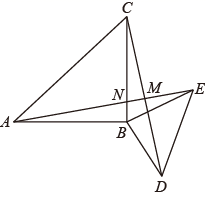
A、① B、② C、③ D、④8. 如图,已知 是平角, 平分 ,在平面上画射线 ,使 和 互余,若 ,则 的度数为( )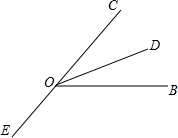 A、 B、 C、 或 D、 或9. 如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=30°,连接AC,BD交于点M,AC与OD相交于E,BD与OA相交于F,连接OM.则下列结论中:①AC=BD;②∠AMB=30°;③△OEM≌△OFM;④MO平分∠BMC.
A、 B、 C、 或 D、 或9. 如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=30°,连接AC,BD交于点M,AC与OD相交于E,BD与OA相交于F,连接OM.则下列结论中:①AC=BD;②∠AMB=30°;③△OEM≌△OFM;④MO平分∠BMC.正确的个数有( )
 A、4个 B、3个 C、2个 D、1个10. 如图 是 的角平分线, 于E,点F,G分别是 , 上的点,且 , 与 的面积分别是10和3,则 的面积是( )
A、4个 B、3个 C、2个 D、1个10. 如图 是 的角平分线, 于E,点F,G分别是 , 上的点,且 , 与 的面积分别是10和3,则 的面积是( ) A、4 B、5 C、6 D、7
A、4 B、5 C、6 D、7二、填空题
-
11. 如图,已知△ABC≌△DEF,则DE=.
 12. 如图,在 中, , 平分 交 于点 , ,垂足为 ,若 , ,则 的长为.
12. 如图,在 中, , 平分 交 于点 , ,垂足为 ,若 , ,则 的长为.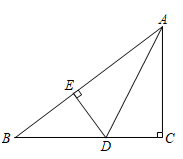 13. 如图所示,△ABC中,∠C=90°,AD平分∠BAC,AB=6,CD=2,则△ABD的面积是.
13. 如图所示,△ABC中,∠C=90°,AD平分∠BAC,AB=6,CD=2,则△ABD的面积是. 14. 将一副三角板按如图拼接,使两斜边重合,取 的中点 ,连接 ,则 .
14. 将一副三角板按如图拼接,使两斜边重合,取 的中点 ,连接 ,则 . 15. 如图,在△ABC中,AB=AC,BD=CE,CD=BF,若∠A=50°,则∠EDF的度数为 .
15. 如图,在△ABC中,AB=AC,BD=CE,CD=BF,若∠A=50°,则∠EDF的度数为 .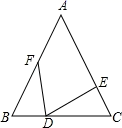 16. 如图,在四边形 中, 于点 ,且 平分 ,若 的面积为 ,则 的面积为 .
16. 如图,在四边形 中, 于点 ,且 平分 ,若 的面积为 ,则 的面积为 .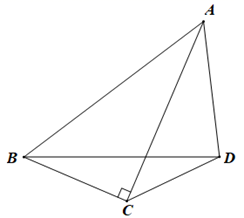
三、解答题
-
17. 我们知道,“对称补缺”的思想是解决与轴对称图形有关的问题时的一种重要的添加辅助线的策略.请参考这种思想,解决本题:如图,在△ABC中,AC=BC , ∠ACB=90°,D是AC上一点,AE⊥BD交BD的延长线于E , 且BD是∠ABC的角平分线.
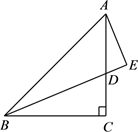
求证:AE= BD .
18. 已知如图,∠A=90°,AB=AC,BD平分∠ABC,CE⊥BD,垂足为E. 求证:BD=2CE. 19. 已知: , , 平分 .求: 的度数.
19. 已知: , , 平分 .求: 的度数.四、作图题
-
20. 已知: 及边 上一点 .求作: ,使得 = .

要求:
(1)、尺规作图,保留作图痕迹,不写作法;(2)、请你写出作图的依据.五、综合题