12.3 角的平分线的性质 同步练习----初中数学人教版八年级上册
试卷更新日期:2021-08-09 类型:同步测试
一、单选题
-
1. 观察下列作图痕迹,所作线段 为 的角平分线的是( )A、
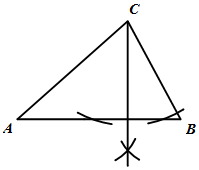 B、
B、 C、
C、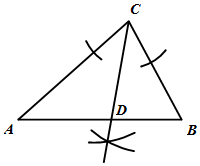 D、
D、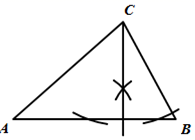 2. 如图,在 中, 平分 ,交 于点D, ,垂足为点E,若 ,则 的长为( )
2. 如图,在 中, 平分 ,交 于点D, ,垂足为点E,若 ,则 的长为( )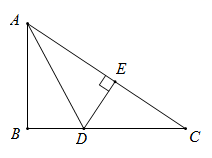 A、 B、1 C、2 D、63. 如图,在 中, , 平分 , 于E,则下列结论中,不正确的是( )
A、 B、1 C、2 D、63. 如图,在 中, , 平分 , 于E,则下列结论中,不正确的是( )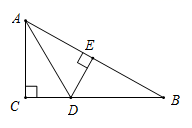 A、 平分 B、 C、 平分 D、4. 如图,已知直线AB//CD,∠GEB 的平分线EF交CD于点F,∠1=30°,则∠2等于( )
A、 平分 B、 C、 平分 D、4. 如图,已知直线AB//CD,∠GEB 的平分线EF交CD于点F,∠1=30°,则∠2等于( ) A、135° B、145° C、155° D、165°5. 如图,在 中, , 平分 , , ,则点D到AC的距离为( )
A、135° B、145° C、155° D、165°5. 如图,在 中, , 平分 , , ,则点D到AC的距离为( ) A、4 B、6 C、8 D、106. 如图,用直尺和圆规作图,以点O为圆心,适当长为半径画弧,分别交OB,OA于点E、D,再分别以点E、D为圆心,大于 ED的长为半径画弧,两弧交于点C,连接OC,则△ODC≌OEC的理由是( )
A、4 B、6 C、8 D、106. 如图,用直尺和圆规作图,以点O为圆心,适当长为半径画弧,分别交OB,OA于点E、D,再分别以点E、D为圆心,大于 ED的长为半径画弧,两弧交于点C,连接OC,则△ODC≌OEC的理由是( )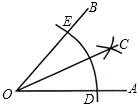 A、SSS B、SAS C、AAS D、HL7. 如图,直线AB∥CD,直线EF分别与AB,CD相交于点E,F,∠BEF的平分线EN与CD相交于点N。若∠1=65°,则∠2=( )
A、SSS B、SAS C、AAS D、HL7. 如图,直线AB∥CD,直线EF分别与AB,CD相交于点E,F,∠BEF的平分线EN与CD相交于点N。若∠1=65°,则∠2=( ) A、64° B、50° C、60° D、54°8. 如图,在 Rt△ACB 中,∠C=90°, AD 平分∠CAB 交BC平D,DE ⊥AB 交AB于E,则下列结论中不正确的是( )
A、64° B、50° C、60° D、54°8. 如图,在 Rt△ACB 中,∠C=90°, AD 平分∠CAB 交BC平D,DE ⊥AB 交AB于E,则下列结论中不正确的是( ) A、BD +ED=BC B、DE 平分∠ADB C、AD 平分∠EDC D、ED+AC>AD9. 如图,在四边形ABCD中,∠A=∠BDC=90°,∠C=∠ADB,点P是BC边上的一动点,连接DP,若AD=4,则DP的长不可能是( )
A、BD +ED=BC B、DE 平分∠ADB C、AD 平分∠EDC D、ED+AC>AD9. 如图,在四边形ABCD中,∠A=∠BDC=90°,∠C=∠ADB,点P是BC边上的一动点,连接DP,若AD=4,则DP的长不可能是( ) A、6 B、5 C、4 D、310. 如图,在△ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+ ∠C;②当∠C=60°时,AF+BE=AB; ③若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是( )
A、6 B、5 C、4 D、310. 如图,在△ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+ ∠C;②当∠C=60°时,AF+BE=AB; ③若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是( ) A、①② B、②③ C、①②③ D、①③
A、①② B、②③ C、①②③ D、①③二、填空题
-
11. 如图,点 是 的平分线 上一点, ,若 ,则 的度数为.
 12. 如图,在△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,已知AC=3,AD=2,则点D到AB边的距离为.
12. 如图,在△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,已知AC=3,AD=2,则点D到AB边的距离为.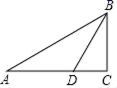 13. 如图,在 中, 是 的角平分线, ,垂足为E,若 .
13. 如图,在 中, 是 的角平分线, ,垂足为E,若 .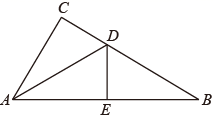 14. 如图,在 中, ,以点 为圆心,任意长为半径画弧,分别交 , 于点 , ,再分别以点 , 为圆心,大于 长为半径画弧,两弧交于点 ,作射线 ,交 于点 .已知 , ,则点 到 的距离为.
14. 如图,在 中, ,以点 为圆心,任意长为半径画弧,分别交 , 于点 , ,再分别以点 , 为圆心,大于 长为半径画弧,两弧交于点 ,作射线 ,交 于点 .已知 , ,则点 到 的距离为. 15. 如图,已知直线AB、CD相交与点O,如果∠BOD=40°,OA平分∠COE,那么∠DOE=.
15. 如图,已知直线AB、CD相交与点O,如果∠BOD=40°,OA平分∠COE,那么∠DOE=.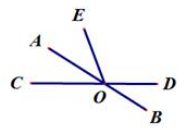 16. 如图,△ABC中∠BAC=60°,将△ACD沿AD折叠,使得点C落在AB上的点C′处,连接C′D与C′C,∠ACB的角平分线交AD于点E;如果BC′=DC′;那么下列结论:①∠1=∠2;②AD垂直平分C′C;③∠B=3∠BCC′;④DC∥EC;其中正确的是:;(只填写序号)
16. 如图,△ABC中∠BAC=60°,将△ACD沿AD折叠,使得点C落在AB上的点C′处,连接C′D与C′C,∠ACB的角平分线交AD于点E;如果BC′=DC′;那么下列结论:①∠1=∠2;②AD垂直平分C′C;③∠B=3∠BCC′;④DC∥EC;其中正确的是:;(只填写序号)
三、解答题
-
17. 如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8,若S△ABC=28,求DE的长.
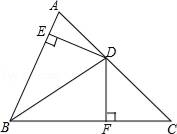 18. 如图,已知 平分 , .求证: .
18. 如图,已知 平分 , .求证: . 19. 如图,已知BE平分∠ABC,点D在射线BA上,且∠ABE=∠BED,若∠ABE=25°时,求∠ADE的度数.
19. 如图,已知BE平分∠ABC,点D在射线BA上,且∠ABE=∠BED,若∠ABE=25°时,求∠ADE的度数.
四、作图题
-
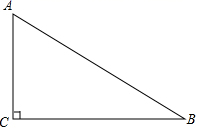
20. 如图,在 中, ,用尺规在 上求作一点 ,使 到边 , 的距离相等(不写作法,保留作图痕迹).
五、综合题
-
21. 探索角的平分线的画法.(1)、画法1:利用直尺和圆规
请在图中用直尺和圆规画出 的平分线 ;(不写画法不需证明,保留作图痕迹)
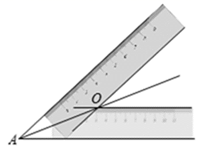
 (2)、画法2:利用等宽直尺.
(2)、画法2:利用等宽直尺.如图,将一把等宽直尺的一边依次落在 的两条边上,再过另一边分别画直线,两条直线相交于点O.画射线 ,则射线 是 的平分线.这种角的平分线的画法依据的是______.
 A、 B、 C、 D、(3)、画法3:利用刻度尺
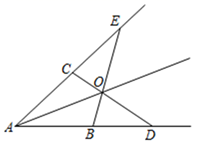
A、 B、 C、 D、(3)、画法3:利用刻度尺已知:如图,在 的两条边上分别画 , ,连接 、 ,交点为点O,画射线 .
求证: 是 的平分线.
 (4)、画法4:利用你手里带有刻度的一块直角三角尺,设计一种与上述画法不同的角的平分线的画法.请在图中画出 的平分线 ,写出画法,并加以证明.
(4)、画法4:利用你手里带有刻度的一块直角三角尺,设计一种与上述画法不同的角的平分线的画法.请在图中画出 的平分线 ,写出画法,并加以证明.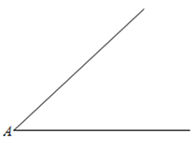 22. 如图1,点A、B分别在射线 、 上运动(不与点O重台), 、 分别是 和 的角平分线, 延长线交 于点G .
22. 如图1,点A、B分别在射线 、 上运动(不与点O重台), 、 分别是 和 的角平分线, 延长线交 于点G .
 (1)、若 ,则 ;(直接写出答案)(2)、若 ,求出 的度数;(用含n的代数式表示)(3)、如图2.若 ,过点C作 交 于点F , 求 与 数量关系.
(1)、若 ,则 ;(直接写出答案)(2)、若 ,求出 的度数;(用含n的代数式表示)(3)、如图2.若 ,过点C作 交 于点F , 求 与 数量关系.
-