第十一章 三角形 数学活动 镶嵌----初中数学人教版八年级上册
试卷更新日期：2021-08-09 类型：同步测试
一、单选题
-
1. 用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是平面图形的镶嵌.工人师傅不能用下列哪种形状、大小完全相同的一种地砖在平整的地面上镶嵌（ ）A、等边三角形 B、正方形 C、正五边形 D、正六边形2. 用正三角形和正六边形铺地面，设在一个顶点周围有m个正三角形，有n个正六边形，则m ， n满足的关系式是（ ）A、m+n＝8 B、2m+n＝6 C、2m+3n＝12 D、m+2n＝63. 正多边形通过镶嵌能够密铺成一个无缝隙的平面，下列组合中不能镶嵌成一个平面的是（ ）A、正三角形和正方形 B、正三角形和正六边形 C、正方形和正六边形 D、正方形和正八边形4. 如图，若干全等正五边形排成形状，图中所示的是前3个正五边形，则要完成这一圆环还需这样的正五边形（ ）
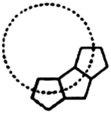A、6个 B、7个 C、9个 D、10个5. 嘉淇用一些完全相同的 纸片，已知六个 纸片按照图1所示的方法拼接可得外轮廓是正六边形图案，若用 个 纸片按图2所示的方法拼接，那么可以得到外轮廓的图案是（ ）
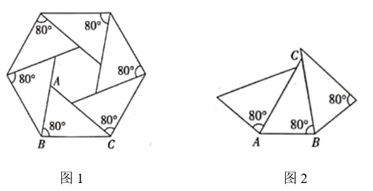A、正十二边形 B、正十边形 C、正九边形 D、正八边形6. 分别剪一些边长相同的①正三角形，②正方形，③正五边形，④正六边形，如果用其中一种正多边形镶嵌，可以镶嵌成一个平面图案的有（ ）A、①②③ B、②③④ C、①②④ D、①②③④都可以7. 如图，张明同学设计了四种正多边形的瓷砖图案，在这四种瓷砖图案不能铺满地面的是（ ）A、
B、
C、
D、
二、填空题
-
8. 现有①正三角形、②正方形、③正五边形三种形状的地砖，只选取其中一种地砖镶嵌地面，不能进行地面镶嵌的有（填序号）．9. 如图所示是三个边长相等的正多边形拼成的无缝隙、不重叠的图形的一部分，正多边形①和②的内角都是108°，则正多边形③的边数是 ．
10. 在数学活动课中我们学习过平面镶嵌.若给出下面一些边长均为1的正三角形、正大边形卡片。要求必须同时使用这两种卡片，不重叠、无继隙，围绕某一个顶点拼在一起，成一个平面图案，则共拼出种不同的图案：其中所拼的图案中最大的周长为.
11. 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时，就能拼成一个既不留空隙，又不相互重叠的平面图形，我们称之为镶嵌．用一种或几种正多边形镶嵌平面有多种方案，如：6个正三角形，记作（3，3，3，3，3，3）；3个正六边形，记作（6，6，6）；又如，（3，3，6，6）表示2个正三角形和2个正六边形的组合．请你再写出除了以上所举的三例以处的三种方案： ．12. 如图是以正八边形为“基本单位”铺成的图案的一部分，（其中有4×3个“基本单位”），其间存有若干个小正方形空隙，以及图案的4个角处有更小的三角形空隙，若密铺5×4个“基本单位”的图案，并填满空隙，则需要个小正方形，小三角形．（不含图案的4个角）
三、综合题
-
13. 在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案．也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里叫做平面镶嵌）．这显然与正多边形的内角大小有关．当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角（360°）时，就拼成了一个平面图形．
(1)、请根据下列图形，填写表中空格：正多边形边数
3
4
5
6
…
正多边形每个内角的度数
…
(2)、如图，如果限于用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形；(3)、正三角形，正四边形，正六边形中选一种，再在其他正多边形中选一种，请画出用这两种不同的正多边形镶嵌成的一个平面图形（草图）；并探索这两种正多边形共能镶嵌成几种不同的平面图形？说明你的理由．