11.2 与三角形有关的角 同步练习----初中数学人教版八年级上册
试卷更新日期：2021-08-09 类型：同步测试
一、单选题
-
1. 如图，直线AB∥CD，∠B＝50°，∠D＝20°，则∠E的度数是（ ）
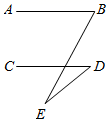A、20° B、30° C、50° D、70°2. 如图，将含30°角的直角三角板ABC放在平行线α和b上，∠C＝90°，∠A＝30°，若∠1＝20°，则∠2的度数等于（ ）
A、60° B、50° C、40° D、30°3. 如图，已知AB∥CD，∠1＝125°，∠2＝55°，则∠C＝（ ）
A、45° B、50° C、70° D、65°4. 如图， ， ，∠CAD=60°， 的度数等于（ ）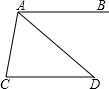
A、60° B、50° C、45° D、40°5. 如图，将一副三角尺按图中所示位置摆放，点 在 上，其中 ， ， ， ， ，则 的度数是（ ）
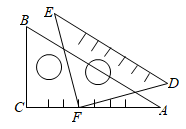A、 B、 C、 D、6. 一副三角板如图所示摆放，若 ，则 的度数是（ ）
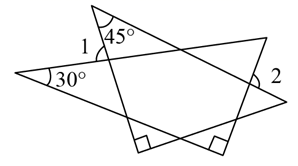A、80° B、95° C、100° D、110°7. 如图， 中， ， ， ，则 的度数是（ ）
A、 B、 C、 D、8. 若三角形三个内角度数比为2：3：5，则这个三角形一定是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定9. 如图，△ABC中，∠ACB=90°，D为AB上任一点，过D作AB的垂线，分别交边AC、BC的延长线于EF两点，∠BAC∠BFD的平分线交于点I，AI交DF于点M，FI交AC于点N，连接BI.下列结论：①∠BAC=∠BFD；②∠ENI=∠EMI；③AI⊥FI；④∠ABI=∠FBI；其中正确结论的个数是（ ）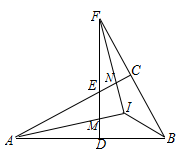
A、1个 B、2个 C、3个 D、4个二、填空题
-
10. 在 中， ，则 等于.11. 如果三角形的一个外角等于与它相邻的内角的5倍，等于与它不相邻的一个内角的3倍.则此三角形最大内角是度.12. 如图，在△ABC中，∠C=90°，点D在AC上，DE∥AB，若∠CDE=165°，则∠B的度数为.
13. 如图，点D在AB上，点E在AC上，BE、CD相交于点O，∠A=40°，∠C=30°，∠BOD=100°.则∠B=°.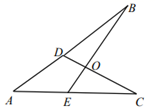
14. 一副三角尺ABC， DEF拼接成如图所示的图形，其中∠B=30°∠D=45°，DF经过点A，两斜边AB与DE互相平行，则∠CAF= 度
15. 如图， .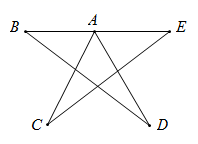
16. 已知△ABC中，∠A=60°，∠ACB=40°，D为BC边延长线上一点，BM平分∠ABC，E为射线BM上一点.若直线CE垂直于△ABC的一边，则∠BEC=°.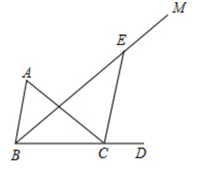
三、解答题
-
17. 如图，在Rt△ABE中，∠AEB=90°，C为.A延长线上的一点，D为AB边上的一点，DC交BE于F，若∠ADC=80"，∠B=30°，求∠C的度数.
18. 如图，在△ABC中，∠B＝80°，∠C＝30°，AD⊥BC于点D，AE平分∠BAC，求∠EAD的度数．
19. 如图，一条直线分别交△ABC的边及延长线于D、E、F． ∠A=20°， ∠CED=100°， ∠ADF=35°．求 ∠B的大小．
四、综合题
