11.2.2 三角形的外角 同步练习----初中数学人教版八年级上册
试卷更新日期:2021-08-09 类型:同步测试
一、单选题
-
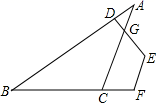
1. 将一副三角板按如图方式重叠,则 的度数为( )
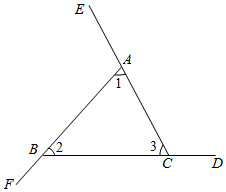
 A、 B、 C、 D、2. 如图,直线 ,则 ( )
A、 B、 C、 D、2. 如图,直线 ,则 ( )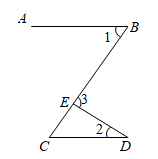 A、 B、 C、 D、3. 三角板是我们学习数学的工具,一副三角板拼成如图方式,则图中 的值为( )
A、 B、 C、 D、3. 三角板是我们学习数学的工具,一副三角板拼成如图方式,则图中 的值为( )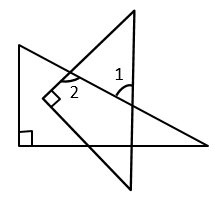 A、30° B、45° C、60° D、不能确定4. 如图,已知 ,则 的值( )
A、30° B、45° C、60° D、不能确定4. 如图,已知 ,则 的值( ) A、不确定 B、等于1 C、等于2 D、大于25. 如图,已知直线 、 、 两两相交,且 .若 ,则 的度数为( )
A、不确定 B、等于1 C、等于2 D、大于25. 如图,已知直线 、 、 两两相交,且 .若 ,则 的度数为( )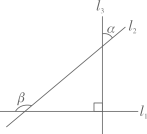 A、 B、 C、 D、6. 如图所示,直线a、b被直线c、d所截,且a//b,c与d相交于点O,则α=( )
A、 B、 C、 D、6. 如图所示,直线a、b被直线c、d所截,且a//b,c与d相交于点O,则α=( ) A、11° B、33° C、43° D、68°7. 如图,l1∥l2 , ∠1=120°,∠2=100°,则∠3等于( )
A、11° B、33° C、43° D、68°7. 如图,l1∥l2 , ∠1=120°,∠2=100°,则∠3等于( ) A、60° B、50° C、40° D、20°8. 如图,在 中, , 是 内角 的平分线, 是 外角 的平分线, 是 外角 的平分线,以下结论不正确的是( )
A、60° B、50° C、40° D、20°8. 如图,在 中, , 是 内角 的平分线, 是 外角 的平分线, 是 外角 的平分线,以下结论不正确的是( ) A、 B、 C、 D、 平分
A、 B、 C、 D、 平分二、填空题
-
9. 如图,直线a∥b , 在Rt△ABC中,点C在直线a上,若∠1=53°,∠A=30°,则∠2=°.
 10. 如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=.
10. 如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=. 11. 如图所示,∠1,∠2 的大小关系是∠1∠2.
11. 如图所示,∠1,∠2 的大小关系是∠1∠2. 12. 欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是°.
12. 欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是°. 13. 如图,直线 ,直线 分别与 ,PQ交于点A,B,小宇同学利用尺规按以下步骤作图:①以点 为圆心,以任意长为半径作弧交 于点 ,交AB于点 ,②分别以C、D为圆心,以大于 长为半径作弧,两弧在 内交于点 ;③作射线 交 于点F,若∠ABP=70°,则 .
13. 如图,直线 ,直线 分别与 ,PQ交于点A,B,小宇同学利用尺规按以下步骤作图:①以点 为圆心,以任意长为半径作弧交 于点 ,交AB于点 ,②分别以C、D为圆心,以大于 长为半径作弧,两弧在 内交于点 ;③作射线 交 于点F,若∠ABP=70°,则 .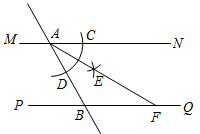 14. 如图,在△ABC中,∠A=64°,∠ABC和∠ACD的平分线交于点A1 , 得∠A1;∠A1BC和∠A1CD的平分线交于点A2 , 得∠A2;…依次类推,则∠A4=度.
14. 如图,在△ABC中,∠A=64°,∠ABC和∠ACD的平分线交于点A1 , 得∠A1;∠A1BC和∠A1CD的平分线交于点A2 , 得∠A2;…依次类推,则∠A4=度.
三、解答题
-
15. 将一副直角三角尺 和 如图放置,其中 , , ,若 ,试判断 与 的位置关系,并说明理由.