山东省临沂市平邑县2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-08-09 类型:期末考试
一、单选题
-
1. 在31415926.4, ,2π, , ,0.1010010001…,这6个数中,无理数有( )A、2个 B、3个 C、4个 D、5个2. 下列调查中,调查方式选择不合理的是( )A、为了了解某学校七年级女生的身高情况,选择全面调查 B、为了了解某公园全年的游客流量,选择抽样调查 C、为了了解神舟飞船的零件的质量情况,选择抽样调查 D、为了了解一批节能灯使用寿命情况,选择抽样调查3. 下列变形中错误的是( )A、由a>b得a﹣c>b﹣c B、由﹣a>﹣b得a>b C、由2x>3得x D、由 y得x<﹣2y4. 如图,直线a//b , 点B在直线a上,且AB⊥BC , ∠2=55°,则∠1的度数为( )
 A、35° B、45° C、55° D、50°5. 如图,直角△ABC沿BC方向平移到△DEF的位置,平移的距离为8,AB=6,则图中四边形ACFD的面积是( )
A、35° B、45° C、55° D、50°5. 如图,直角△ABC沿BC方向平移到△DEF的位置,平移的距离为8,AB=6,则图中四边形ACFD的面积是( ) A、24 B、36 C、48 D、以上答案都不对6. 9的平方根是( )A、 3 B、 C、-3 D、97. 点A为直线a外一点,点B是直线a上点,点A到直线a的距离为5,则AB的长度一定不是( )A、10 B、8 C、5 D、38. 在平面直角坐标系的第四象限内有一点P,点P到x轴的距离为4,到y轴的距离为3,则点P的坐标是( )A、(3,﹣4) B、(4,﹣3) C、(﹣4,3) D、(﹣3,4)9.
A、24 B、36 C、48 D、以上答案都不对6. 9的平方根是( )A、 3 B、 C、-3 D、97. 点A为直线a外一点,点B是直线a上点,点A到直线a的距离为5,则AB的长度一定不是( )A、10 B、8 C、5 D、38. 在平面直角坐标系的第四象限内有一点P,点P到x轴的距离为4,到y轴的距离为3,则点P的坐标是( )A、(3,﹣4) B、(4,﹣3) C、(﹣4,3) D、(﹣3,4)9.一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )
 A、﹣1<x≤2 B、﹣1≤x<2 C、﹣1<x<2 D、无解10. 已知方程组 ,则2x+6y的值是( )A、﹣2 B、2 C、﹣4 D、411. 移动通讯行业人员想了解5G手机的使用情况,在某高校随机对500位大学生进行了问卷调查,结果其中有20位使用了5G手机.下列关于该调查说法错误的是( )A、该调查方式是抽样调查 B、样本是20位大学生 C、样本容量是500 D、5G手机在该高校的使用率约是4%12. 一副直角三角尺如图摆放,点 在 的延长线上, , , , ,则∠ 的度数是( )
A、﹣1<x≤2 B、﹣1≤x<2 C、﹣1<x<2 D、无解10. 已知方程组 ,则2x+6y的值是( )A、﹣2 B、2 C、﹣4 D、411. 移动通讯行业人员想了解5G手机的使用情况,在某高校随机对500位大学生进行了问卷调查,结果其中有20位使用了5G手机.下列关于该调查说法错误的是( )A、该调查方式是抽样调查 B、样本是20位大学生 C、样本容量是500 D、5G手机在该高校的使用率约是4%12. 一副直角三角尺如图摆放,点 在 的延长线上, , , , ,则∠ 的度数是( )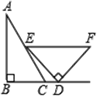 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 的立方根是 .14. 在平面直角坐标系中,已知点A(﹣2,4)、B(3,m),若直线AB∥x轴,则m的值为 .
15. 若a 2<b , a , b是两个连续的整数,则b= .16. 若方程组 的解中 ,则k等于;17. 抽样调查是一种用样本估计总体的很好的统计方法.小明的家承包了村里的一个鱼塘用来养鱼,养殖一年后小明爸爸准备将养的鱼一次性整塘出售给某鱼店老板,为此,小明爸爸想估计一下整塘鱼的数量.小明运用所学习的统计知识进行了一下操作:他首先从鱼塘中随机排捞出100条鱼,将这100条鱼分别作一记号后再放回鱼塘,数天后再从鱼塘中随机捕捞出240条鱼,其中有记号的鱼有15条,这样小明就帮爸爸估算出了鱼塘中鱼的数量.那么小明估计鱼塘中的鱼大约有 条.18. 幸福超市某天卖出39支牙刷和21盒牙膏,收入396元;另一天,以同样的价格卖出同样的52支牙刷和28盒牙膏,则应收入元.19. 如图所示,在平面直角坐标系中,点 , , ,则四边形ABCO的面积为 . 20. “输入一个实数 x,然后经过如图的运算,到判断是否大于 190 为止”叫做一次操作,那么恰好经过三次操作停止,则x的取值范围是 .
20. “输入一个实数 x,然后经过如图的运算,到判断是否大于 190 为止”叫做一次操作,那么恰好经过三次操作停止,则x的取值范围是 .
三、解答题
-
21.(1)、计算: (﹣1)2×|﹣2| ;(2)、解不等式(3x﹣4)﹣3(2x+1)<﹣1;(3)、解方程组 ;(4)、解不等式组 .22. 如图,AB∥CD,∠A=∠D,判断AF与ED的位置关系,并说明理由.
 23. 如图,是小明所在学校的平面示意图,已知宿舍楼的位置是(3,4),艺术楼的位置是(﹣3,1).
23. 如图,是小明所在学校的平面示意图,已知宿舍楼的位置是(3,4),艺术楼的位置是(﹣3,1).
⑴根据题意,画出相应的平面直角坐标系;
⑵分别写出教学楼、体育馆的位置;
⑶若学校行政楼的位置是(﹣1,﹣1),在图中标出行政楼的位置.
24. 如图,已知∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.
证明:∵ DE⊥BC,AB⊥BC(已知)
∴∠DEC=∠ABC=90°( ▲ )
∴DE∥AB( ▲ )
∴∠2= ▲ ( ▲ )
∠1= ▲ ( ▲ )
又∵∠1=∠2( ▲ )
∴∠A=∠3( ▲ )
25. 在党和国家的符合题意领导下,新冠肺炎在中国被得到有效控制,为了了解全市市民对“居家生活和戴口罩”的认识,市调查队随机抽取了10﹣60岁的m名市民进行了调查,并对所抽取的各年龄段的人数数据进行分组整理并绘制成了下列不完整的图表.组别
年龄段
频数
一组
10≤x<20
670
二组
20≤x<30
a
三组
30≤x<40
550
四组
40≤x<50
500
五组
50≤x<60
780

 (1)、求出m和a的值;(2)、求第3组人数在扇形统计图中所对应的圆心角的度数;(3)、假设该市现有10~60岁的市民300万人,问10~20岁年龄段约有多少人?26. 在一次高速铁路建设中,某渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方.已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方31吨,5辆大型渣土运输车与6辆小型渣土运输车一次共运输土方70吨.(1)、一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?(2)、该渣土运输公司决定派出大、小两种型号渣土运输车共20辆参与运输土方,若每次运输土方总量不小于148吨,且小型渣土运输车至少派出2辆,则有哪几种派车方案?
(1)、求出m和a的值;(2)、求第3组人数在扇形统计图中所对应的圆心角的度数;(3)、假设该市现有10~60岁的市民300万人,问10~20岁年龄段约有多少人?26. 在一次高速铁路建设中,某渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方.已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方31吨,5辆大型渣土运输车与6辆小型渣土运输车一次共运输土方70吨.(1)、一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?(2)、该渣土运输公司决定派出大、小两种型号渣土运输车共20辆参与运输土方,若每次运输土方总量不小于148吨,且小型渣土运输车至少派出2辆,则有哪几种派车方案?