山东省东营市垦利区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-08-09 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $a < b$ ，下列式子不成立的是 $($ $)$

A、 $a + 1 < b + 1$ B、 $3 a < 3 b$ C、 $- \frac{1}{2} a > - \frac{1}{2} b$ D、如果 $c < 0$ ，那么 $\frac{a}{c} < \frac{b}{c}$

查看试题解析
2. 下列命题是真命题的是（）

A、相等的角是对顶角 B、线段垂直平分线上的点到这条线段两端点的距离相等 C、若实数a ， b满足a²＝b² ，则a＝b D、若实数a ， b满足a＜0，b＜0，则ab＜0

查看试题解析
3. 不等式3－x＜2x＋6的解集在数轴上表示正确的是（）

A、 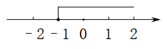B、 C、 D、

查看试题解析
4. 如图，直线a∥b ，在Rt△ABC中，点C在直线a上，若∠1＝58°，∠2＝24°，则∠B的度数为（）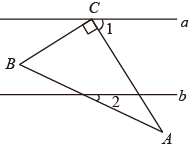

A、56° B、34° C、36° D、24°

查看试题解析
5. 如图，在△ABC中，∠ABC＝90°，AB＝CB ， F为AB延长线一点，点E在BC上，且AE＝CF ， ∠CAE＝30°，则∠ACF的度数是（）

A、75° B、60° C、55° D、45°

查看试题解析
6. 一个两位数，个位与十位的数字之和是11；如果原数加45，等于此两位数的数字位置对调后得到的新的两位数，那么原数是多少？若设原数十位数字为x ，个位数字为y ，则列出的方程组应为（）

A、 ${\begin{array}{l} 10 x + y = 11 \\ 10 x + y + 45 = 10 y + x \end{array}$ B、 ${\begin{array}{l} 10 x + y = 11 \\ x + y + 45 = y + x \end{array}$ C、 ${\begin{array}{l} x + y = 11 \\ 10 x + y + 45 = 10 y + x \end{array}$ D、以上均不对

查看试题解析
7. 如图，一次函数y＝2x和y＝ax+4的图象相交于点A（m，3），则关于x，y的方程组 ${\begin{matrix} y = 2 x \\ y = a x + 4 \end{matrix}$ 的解为（）

A、 ${\begin{matrix} x = \frac{3}{2} \\ y = 3 \end{matrix}$ B、 ${\begin{matrix} x = 3 \\ y = \frac{3}{2} \end{matrix}$ C、 ${\begin{matrix} x = 3 \\ y = 2 \end{matrix}$ D、 ${\begin{matrix} x = 2 \\ y = 3 \end{matrix}$

查看试题解析
8. 如图，在3×3的正方形网格中，已有两个小正方形被涂黑，再将图中剩余的编号1－5的小正方形中任意一个涂黑，则所得图案是一个轴对称图形的概率是（）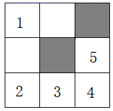

A、1 B、 $\frac{4}{5}$ C、 $\frac{3}{5}$ D、 $\frac{2}{5}$

查看试题解析
9. 已知 ${\begin{matrix} x = 2 \\ y = - 1 \end{matrix}$ 是关于x，y的二元一次方程组 ${\begin{matrix} a x + b y = - 5 \\ 2 b x - a y = 2 \end{matrix}$ 的解，则a＋b的值为（）

A、﹣5 B、﹣1 C、3 D、7

查看试题解析
10. 如图，在△AOB和△COD中，OA＝OB ， OC＝OD ， OA＜OC ， ∠AOB＝∠COD＝36°．连接AC ， BD交于点M ，连接OM ．下列结论：
①∠AMB＝36°，②AC＝BD ， ③OM平分∠AOD ， ④MO平分∠AMD ．其中正确的结论个数有（）个．

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 以方程组 ${\begin{cases} y = 2 x + 2 \\ y = - x + 1 \end{cases}$ 的解为坐标的点（x，y）在第象限．

查看试题解析
12. 把命题“在同一平面内，垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式为．

查看试题解析
13. 如图，△ABC是等边三角形，AD∥BC，CD⊥AD，若AD＝2 cm ，则△ABC的周长为cm.

查看试题解析
14. 若不等式组 ${\begin{array}{l} x \geq 2 a - 1 \\ x < a + 1 \end{array}$ 无解，则a的取值范围是

查看试题解析
15. 如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画弧，分别交AC ， AB于点M ， N ，再分别以点M ， N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P ，作射线AP交边BC于点D ，若CD＝4，AB＝15，则△ABD的面积是．

查看试题解析
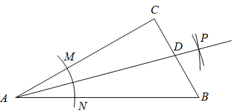16. 一次函数y=ax+b与正比例函数y=kx在同一平面直角坐标系的图象如图所示，则关于x的不等式ax+b≥kx的解集为．

查看试题解析
17. 如果关于x、y的方程组 ${\begin{array}{l} x + 2 y = m \\ x - y = 4 m \end{array}$ 的解是二元一次方程3x＋2y＝14的一个解，那么m的值是．

查看试题解析
18. 如图，已知射线OC上的任意一点到∠AOB的两边的距离都相等，点D、E、F分别为边OC、OA、OB上，如果要想证得OE=OF，只需要添加以下四个条件中的某一个即可，请写出所有可能的条件的序号．
①∠ODE=∠ODF；②∠OED=∠OFD；③ED=FD；④EF⊥OC．

查看试题解析

三、解答题

19.

(1)、解方程组： ${\begin{array}{l} x + y = 16 ， \\ 5 x + 3 y = 72. \end{array}$

(2)、解不等式组： ${\begin{array}{l} \frac{2 x - 1}{3} - \frac{5 x + 1}{2} \leq 1 \\ 5 x - 1 < 3(x + 1) \end{array}$ 并把它的解集表示在数轴上．

查看试题解析
20. 为了提高学生的保护环境意识，某校学生会利用课余时间，组织七、八年级共50名同学参加环保活动，七年级学生平均每人收集10个废弃塑料瓶，八年级学生平均每人收集20个废弃塑料瓶．若所收集的塑料瓶总数不少于800个，至少有多少名八年级学生参加活动？

查看试题解析
21. 如图，点C在线段AB上，AD∥EB ， AC＝BE ， AD＝BC ． CF平分∠DCE ．求证：

(1)、△ACD≌△BEC；

(2)、CF⊥DE ．

查看试题解析
22. 小明和小亮做摸牌游戏，游戏规则为：从形状、大小完全相同的，印有2，3，4，5，4，6，7，9的8张扑克牌中任摸一张，摸到比5大的牌，小明赢；否则，小亮赢．

(1)、求小明摸到4的概率；

(2)、你认为这种游戏规则对他俩公平吗？请你说明理由．若不公平，请你修改游戏规则，使游戏对双方都公平．

查看试题解析
23. 某生态体验园推出了甲、乙两种消费卡，设入园次数为x时所需费用为y元，选择这两种卡消费时，y与x的函数关系如图所示，解答下列问题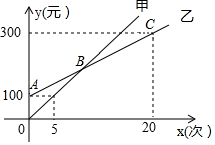

(1)、分别求出选择这两种卡消费时，y关于x的函数表达式；

(2)、请根据入园次数确定选择哪种卡消费比较合算．

查看试题解析
24. 东营某中学为提升校园体育运动多样性，助力师生“阳光运动”，学校决定采购一批排球和足球，采购员在某体育用品商店咨询了排球和足球的售价具体信息：购买2个排球和3个足球共需460元，购买3个排球和1个足球共需270元．

(1)、求排球和足球的售价分别是多少元？

(2)、若该校计划购进排球和足球共100个，其中排球的数量不超过足球的2倍，请你设计出最省钱的购买方案，并说明理由．

查看试题解析
25. 如图

(1)、如图1，在△ABC中，∠ABC ， ∠ACB的平分线交于点O ，过点O作EF∥BC分别交AB ， AC于点E ， F ．直接写出线段EF与BE ， CF之间的数量关系：．

(2)、如图2，若△ABC外角平分线BO和CO交于点O ，过点O作OE∥BC分别交边AB和AC的延长线于点E和F ．线段EF与BE ， CF之间的数量关系是否依然成立？若成立，请说明理由；若不成立，请写出它们之间的数量关系．

(3)、如图3，若△ABC中∠ABC的平分线BO与三角形外角平分线CO交于点O ，过O点作OE∥BC交AB于点E ，交AC于点F ．则EF与BE ， CF之间的数量关系又如何？说明你的理由．

查看试题解析