江西省吉安市吉州区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-08-09 类型：期末考试

进入出卷网下载

一、单选题

1. 如图是常见的安全标记，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $x^{2} + x^{3} = x^{5}$ B、 ${(x + y)}^{2} = x^{2} + y^{2}$ C、 ${(2 x y^{2})}^{3} = 6 x^{3} y^{6}$ D、 $- (x - y) = - x + y$

查看试题解析
3. 下列事件中不是随机事件的是（）

A、打开电视机正好在播放广告 B、明天太阳会从西方升起 C、从课本中任意拿一本书正好拿到数学书 D、从装有黑球和白球的盒子里任意拿出一个球正好是白球

查看试题解析
4.
如图，直线a∥b，∠1=75°，∠2=35°，则∠3的度数是（　　）

A、75° B、55° C、40° D、35°

查看试题解析
5.
如图，向高为H的圆柱形空水杯中注水，表示注水量ｙ与水深ｘ的关系的图象是下面哪一个？（）

A、 B、 C、 D、

查看试题解析
6. 如图，点 $A$ 、 $D$ 在线段 $B C$ 的同侧，连接 $A B$ 、 $A C$ 、 $D B$ 、 $D C$ ，已知 $∠ A B C = ∠ D C B$ ，老师要求同学们补充一个条件使 $Δ A B C ≅ Δ D C B$ ．以下是四个同学补充的条件，其中错误的是 $($ 　　 $)$

A、 $A C = D B$ B、 $A B = D C$ C、 $∠ A = ∠ D$ D、 $∠ A B D = ∠ D C A$

查看试题解析

二、填空题

7. 人体中某种细胞的形状近似看成圆形，其直径约为0.000 002 16米，用科学记数法表示为米.

查看试题解析
8. 已知一等腰三角形的两边长分别为 $2 cm$ 和 $5 cm$ ，则此三角形的周长为 $cm$ ．

查看试题解析
9. 已知 $a + b = 3$ ， $a - b = 2$ ，则 $a^{2} - b^{2} =$ ．

查看试题解析
10. 如图，在长方形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 的交点为O ，长方形的长、宽分别为 $7 cm$ 、 $4 cm$ ， $E F$ 过点O分别交 $A D$ 、 $C B$ 于E、F ，那么图中阴影部分面积为 ${cm}^{2}$ ．

查看试题解析
11. 如图， $A C = B C$ ， $D C = E C$ ， $∠ A C B = ∠ E C D = 90 °$ ，且 $∠ E B D = 50 °$ ，则 $∠ A E B =$

查看试题解析
12. 从点O引出三条射线OA ， OB ， OC ，已知∠AOB=30°，在这三条射线中，当其中一条射线是另两条射线所组成角的平分线时，则∠AOC= ．

查看试题解析

三、解答题

13.

(1)、化简 ${(- a^{2})}^{3} + (- a^{2}) \cdot a^{4}$

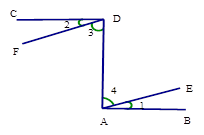
(2)、计算： $- 3^{2} + {(π - 3.14)}^{0} + {(- \frac{1}{3})}^{- 2}$

查看试题解析
14. 如图，已知CD⊥DA，DA⊥AB， ∠1=∠2，试确定直线DF与AE的位置关系，并说明理由。

查看试题解析
15. 先化简，再求值： $(2 x + 1) (2 x - 1) - 5 x (x - 1) + {(x - 1)}^{2}$ ，其中 $x = - \frac{1}{3}$ ．

查看试题解析
16. 在一个不透明的袋中装有2个黄球，3个黑球和5个红球，它们除颜色外其他都相同．

(1)、将袋中的球摇均匀后，求从袋中随机摸出一个球是黄球的概率；

(2)、现在再将若干个红球放入袋中，与原来的10个球均匀混合在一起，使从袋中随机摸出一个球是红球的概率是 $\frac{2}{3}$ ，请求出后来放入袋中的红球的个数．

查看试题解析
17. 仅用无刻度的直尺画图，保留作图痕迹

(1)、在图（1）中的线段 $C D$ 上找一点P ，使点P到A、B两点的距离之和最短；

(2)、在图（2）中画出等腰梯形的对称轴 $M N$

查看试题解析
18. 某课题小组为了了解某品牌电动自行车的销售情况，对某专卖店第一季度该品牌A，B，C，D四种型号的销售做了统计，绘制成如下两幅统计图（均不完整）

(1)、该店第一季度售出这种品牌的电动自行车共多少辆？

(2)、把两幅统计图补充完整；

(3)、若该专卖店计划订购这四款型号的电动自行车1800辆，求C型电动自行车应订购多少辆？

查看试题解析
19. 如图，某校有一块长为（a+b）米，宽为b米的长方形场地（即空白的部分），学校计划把它的各边长都扩大b米，作为健身场地.

(1)、用含 $a$ 、 $b$ 的代数式表示新长方形比原长方形扩大的面积（即阴影部分面积）；

(2)、求出当 $a = 10$ 米， $b = 3$ 米时的阴影部分面积.

查看试题解析
20. 如图，是若干个粗细均匀的铁环最大限度的拉伸组成的链条，已知铁环粗0.8厘米，每个铁环长5厘米，设铁环间处于最大限度的拉伸状态．

求：

(1)、2个、3个、4个铁环组成的链条长分别有多少．

(2)、设n个铁环长为y厘米，请用含n的式子表示y；

(3)、若要组成2.09米长的链条，需要多少个铁环？

查看试题解析
21. 如图1是一个大型的圆形花坛建筑物（其中 $A B$ 与 $C D$ 是一对互相垂直的直径）小川从圆心O出发，按图中箭头所小的方向匀速散步，并保持同样的速度走完下列三条线路：①线段 $O A$ ，②圆弧 $A \to C \to B \to D$ ，③线段 $D O$ 后，回到出发点．记小川所在的位置离出发点的距离为y（即所在位置与点O之间线段的长度）与时间t的关系如图2所示（注：圆周率π取近似值3）根据所给的信息，完成下列各题．

(1)、直接写出 $a =$ ， $b =$ ；

(2)、当 $t \leq 2$ 时，直接写出y与t的关系式；

(3)、在沿途某处小川遇见了他的好朋友小翔并在原地聊了两分钟的时间，然后继续保持原来的速度回到终点O ，请回答：
①小川与小翔的聊天地点位于何处？并求出此时他距离终点O还有多远？

②求他此行总共花了多少分钟的时间？

查看试题解析
22. 代数中的很多等式可以用几何图形直观表示，这种思想叫“数形结合”思想．如：现有正方形卡片A类、B类和长方形C类卡片若干张，如果要拼成一个长为 $2 (a + b)$ ，宽为 $(a + 2 b)$ 的大长方形，可以先计算 $(2 a + b) (a + 2 b) = 2 a^{2} + 5 a b + 2 b^{2}$ ，所以需要A、B、C类卡片2张、2张、5张，如图2所示

(1)、如果要拼成一个长为 $(a + 3 b)$ ，宽为 $(a + b)$ 的大长方形，那么需要A、B、C类卡片各多少张？并画出示意图．

(2)、由图3可得等式：；

(3)、利用（2）中所得结论，解决下面问题，已知 $a + b + c = 11$ ， $a b + b c + a c = 38$ ， $a^{2} + b^{2} + c^{2}$ 的值；

(4)、小明利用2张A类卡片、3张B类卡片和5张长方形C类卡片去拼成一个更大的长方形，那么该长方形的较长的一边长为（用含a、b的代数式表示）

查看试题解析
23. 已知点C为线段 $A B$ 上一点，分别以 $A C$ 、 $B C$ 为边在线段 $A B$ 同侧作 $△ A C D$ 和 $△ B C E$ ，且 $A C = D C$ ， $C B = C E$ ， $∠ A C D = ∠ B C E$ ，直线 $A E$ 与 $B D$ 交于点F ．

(1)、如图①，试说明： $△ A C E ≌ △ D C B$ ；

(2)、如图①，若 $∠ A C D = 60 °$ ，则 $∠ A F B =$ °；如图②，若 $∠ A C D = 90 °$ ，则 $∠ A F B =$ °；如图③，若 $∠ A C D = 120 °$ ，则 $∠ A F B =$ °；

(3)、如图④，若 $∠ A C D = α$ ，求 $∠ A F B$ 的值（用含 $α$ 的代数式表示）；

(4)、若A、B、C三点不在同一直线上，线段 $A C$ 与线段 $B C$ 交于点C（交点F至少在 $B D$ 、 $A E$ 中的一条线），如图⑤，若 $∠ A C D = α$ ，试判断 $∠ A F B$ 与 $α$ 的数量关系，并说明理由．

查看试题解析