云南省昆明市官渡区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列根式中属于最简二次根式的是（）

A、 $\sqrt{a^{2} + 2}$ B、 $\sqrt{\frac{1}{12}}$ C、 $\sqrt{8}$ D、 $\sqrt{27 x^{3}}$

查看试题解析
2. 在平行四边形 $A B C D$ 中， $∠ A + ∠ C = 210^{\circ}$ ，则 $∠ B$ 的度数为（）

A、 $30^{\circ}$ B、 $75^{\circ}$ C、 $95^{\circ}$ D、 $105^{\circ}$

查看试题解析
3. 下列计算正确的是（）．

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 $\sqrt{2} \times \sqrt{5} = \sqrt{7}$ C、 $\sqrt{9} \div \sqrt{3} = 3$ D、 ${(\sqrt{2})}^{2} = 2$

查看试题解析
4. 下列不能表示 $y$ 是 $x$ 的函数的是（）

A、 B、 $y = 2 x + 1$ C、 D、

查看试题解析
5. 悦悦的数学平时成绩为93分，期中考试成绩为94分，期末考试成绩为96分，若按 $3 ： 3 ： 4$ 的比例计算总评成绩，则悦悦的数学总评成绩为（）

A、94 B、94.2 C、94.5 D、95

查看试题解析
6. 下列说法错误的是（）

A、对角线相等的菱形是正方形 B、矩形的对角线相等 C、两组对边分别相等的四边形是平行四边形 D、对角线互相垂直的平行四边形是矩形

查看试题解析
7. 勾股定理是历史上第一个把数与形联系起来的定理，其证明是论证几何的发端．下面四幅图中不能证明勾股定理的是（）

A、 B、 C、 D、

查看试题解析
8. 若关于 $x$ 的一元一次不等式组 ${\begin{array}{l} \frac{2}{3} x > x - 1 \\ 4 x + 1 \geq a \end{array}$ 恰有3个整数解，且一次函数 $y = (a - 2) x + a + 1$ 不经过第三象限，则所有满足条件的整数a的值之和是（）

A、-2 B、-1 C、0 D、1

查看试题解析

二、填空题

9. 若根式 $\sqrt{x - 7}$ 有意义，则实数 $x$ 的取值范围为．

查看试题解析
10. 2020年发布的《云南省初中学生学业水平体育科目考试办法》中，篮球成为三项技能类考试项目之一．某学校甲乙两名同学做了10次定点投篮训练（每次训练投5个），每次训练成绩（投中的个数）如图所示，则甲乙两名同学投篮成绩比较稳定的是（填“甲”或“乙”）．

查看试题解析
11. 如图，△ABC中，AC=5，BC=12，AB=13，CD是AB边上的中线．则CD= ．

查看试题解析
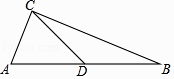12. 如图，直线y=x+2与直线y=ax+c相交于点P（m ， 3），则关于x的不等式x+2≤ax+c的解为．

查看试题解析
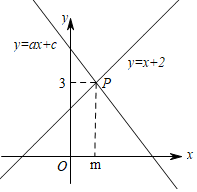13. 如图，在▱ABCD中，按以下步骤作图：①以C为圆心，以适当长为半径画弧，分别交BC ， CD于M ， N两点；②分别以M ， N为圆心，以大于 $\frac{1}{2}$ MN的长为半径画弧，两弧在∠BCD的内部交于点P；⑨连接CP并延长交AD于E ．若AE＝2，CE＝6，∠B＝60°，则ABCD的周长等于．

查看试题解析
14. 在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ， $B C = 2$ ， $D$ 为 $A C$ 中点， $E$ 为边 $A B$ 上一动点，当四边形 $B C D E$ 有一组邻边相等时，则 $A E$ 的长为．

查看试题解析

三、解答题

15. 计算：

(1)、 $(\sqrt{12} + \sqrt{8}) - \sqrt{27}$

(2)、 ${(\sqrt{5} +1)}^{2} - (\sqrt{3} + 1) (\sqrt{3} - 1)$

(3)、 $\sqrt{18} - 4 \sqrt{\frac{1}{2}} - \sqrt{24} \div \sqrt{3}$

查看试题解析
16. 如图，正方形网格中的△ABC，若小方格边长为1，求：

(1)、△ABC的周长；

(2)、△ABC是直角三角形吗？为什么？

查看试题解析

17. 在研发某种新冠疫苗的一次动物实验中，将200只基因编辑小鼠分成20组，每组10只．选取其中10个组作为接种批次，给每只小鼠注射疫苗，其余作为对照批次，不注射疫苗．实验后统计发现，接种批次共有13只小鼠发病，发病率为0.13．对照批次小鼠发病情况如下表所示．

对照批次编号（组）	1	2	3	4	5	6	7	8	9	10
发病小鼠数（只）	3	5	7	3	8	4	8	5	5	6

(1)、①对照批次发病小鼠数的中位数是 ▲ ，众数是 ▲ ；

②求对照批次发病小鼠的总只数；

(2)、流行病学中，疫苗在一定范围内能保护某个群体的机率叫做疫苗保护率，其计算方法是：疫苗保护率＝

\frac{对 照 批 次 发 病 率 - 接 种 批 次 发 病 率}{对 照 批 次 发 病 率}

．由此可得这种新冠疫苗保护率是多少（结果精确到0.01）？

查看试题解析

18. 如图，点 $M 、 N$ 在平行四边形 $A B C D$ 的对角线 $A C$ 上，且 $A M = C N$ ，求证：四边形 $B M D N$ 是平行四边形．

查看试题解析
19. 在平面直角坐标系中，一次函数 $y = k x +b$ （ $k ， b$ 是常数，且上 $k \neq 0$ ）的图象经过点 $(2 ， 1)$ 和 $(- 1 ， 7)$ ．

(1)、求该函数的表达式；

(2)、若点 $P (a - 5 ， 3 a)$ 在该函数的图象上，求点 $P$ 的坐标；

(3)、当 $1 < y < 9$ 时，请直接写出 $x$ 的取值范围．

查看试题解析
20. 阅读下列计算过程：
$\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$

$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$

$\frac{1}{\sqrt{5} + 2} = \frac{1 (\sqrt{5} - 2)}{(\sqrt{5} + 2) (\sqrt{5} - 2)} = \sqrt{5} - 2$

(1)、根据上面运算方法，直接写出 $\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ ；

(2)、利用上面的解法，请化简：
$\frac{1}{\sqrt{2021} + \sqrt{2020}} + \frac{1}{\sqrt{2020} + \sqrt{2019}} + \frac{1}{\sqrt{2019} + \sqrt{2018}} + ... + \frac{1}{\sqrt{2} + 1}$

(3)、根据上面的知识化简 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$

查看试题解析
21. 如图，笔直的公路上A、B两点相距25km，C、D为两村庄，DA⊥AB于点A，CB⊥AB于点B，已知DA=15km，CB=10km，现在要在公路的AB段上建一个土特产品收购站E，使得C、D两村到收购站E的距离相等，则收购站E应建在离A点多远处？

查看试题解析
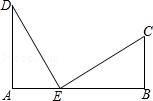22. 为庆祝第二个国际茶日，弘扬云茶文化，做响云茶品牌，云南省“5・21”国际茶日活动在官渡区企业经营管理人才培训基地举办．某茶叶经销商准备参与本次活动．经计算，他销售10千克 $A$ 级茶和20千克 $B$ 级茶的利润为4000元，销售20千克 $A$ 级茶和10千克 $B$ 级茶的利润为3500元．

(1)、求每千克 $A$ 级茶、 $B$ 级茶的利润分别为多少元？

(2)、若该经销商一次决定购进 $A 、 B$ 两种级别的茶叶共200千克用于销售，设购进 $A$ 级茶 $m$ 千克，销售总利润为 $w$ 元．
①求 $w$ 与 $m$ 之间的函数关系式；

②若其中 $B$ 级茶叶的进货量不超过 $A$ 级茶叶的3倍，请你帮该经销商设计一种进货方案使销售总利润最大，并求出总利润的最大值．

查看试题解析
23. 如图，将平行四边形 $D B E C$ 沿 $B D$ 折叠，点 $C$ 恰好落在 $E B$ 的延长线上点 $A$ 处，连接 $A C ， B D$ 交于点 $O$ ．

(1)、证明：四边形 $A B C D$ 是菱形；

(2)、若 $A C = 6 ， B D = 8$ ．
①求 $Δ A C E$ 的面积；

②若直线 $A E$ 上有一点 $F$ ，当 $Δ F C E$ 为等腰三角形时，直接写出线段为 $A F$ 的长．

查看试题解析