山东省枣庄市薛城区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-09 类型:期末考试
一、单选题
-
1. 若分式 中x和y的值都扩大到原来的2倍,则分式的值( )A、扩大到原来的2倍 B、扩大到原来的4倍 C、缩小到原来的 D、不变2. 如图,将 绕边 的中点O顺时针旋转180°.嘉淇发现,旋转后的 与 构成平行四边形,并推理如下:
点A,C分别转到了点C,A处,
而点B转到了点D处.
∵ ,
∴四边形 是平行四边形.
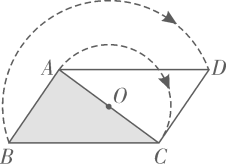
小明为保证嘉淇的推理更严谨,想在方框中“∵ ,”和“∴四边形……”之间作补充.下列正确的是( )
A、嘉淇推理严谨,不必补充 B、应补充:且 , C、应补充:且 D、应补充:且 ,3. 如图,已知等腰 的底角 ,顶点B到边AC的距离是3cm,则AC的长为( ) A、3cm B、 C、 D、4. 把式子2x(a﹣2)﹣y(2﹣a)分解因式,结果是( )A、(a﹣2)(2x+y) B、(2﹣a)(2x+y) C、(a﹣2)(2x﹣y) D、(2﹣a)(2x﹣y)5. 小红同学在某数学兴趣小组活动期间,用铁丝设计并制作了如图所示的三种不同的图形,请您观察甲、乙、丙三个图形,判断制作它们所用铁丝的长度关系是( )
A、3cm B、 C、 D、4. 把式子2x(a﹣2)﹣y(2﹣a)分解因式,结果是( )A、(a﹣2)(2x+y) B、(2﹣a)(2x+y) C、(a﹣2)(2x﹣y) D、(2﹣a)(2x﹣y)5. 小红同学在某数学兴趣小组活动期间,用铁丝设计并制作了如图所示的三种不同的图形,请您观察甲、乙、丙三个图形,判断制作它们所用铁丝的长度关系是( )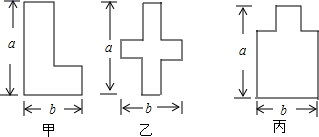 A、制作甲种图形所用铁丝最长 B、制作乙种图形所用铁丝最长 C、制作丙种图形所用铁丝最长 D、三种图形的制作所用铁丝一样长6. 下面的计算过程中,从哪一步开始出现错误( ).
A、制作甲种图形所用铁丝最长 B、制作乙种图形所用铁丝最长 C、制作丙种图形所用铁丝最长 D、三种图形的制作所用铁丝一样长6. 下面的计算过程中,从哪一步开始出现错误( ).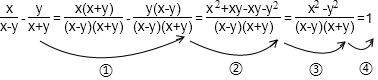 A、① B、② C、③ D、④7. 如图,已知四边形 中, 是 边上的一个动点, 是 边上的一个定点, , 分别是 , 的中点,当 点 在上从 向 逐渐移动时,下列结论成立的是( )
A、① B、② C、③ D、④7. 如图,已知四边形 中, 是 边上的一个动点, 是 边上的一个定点, , 分别是 , 的中点,当 点 在上从 向 逐渐移动时,下列结论成立的是( )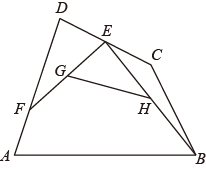 A、线段 的长逐渐增大 B、线段 的长逐渐减少 C、线段 的长保持不变 D、线段 的长先增大后减小8. 如图 是正五边形 的三个外角,若 则 =( )
A、线段 的长逐渐增大 B、线段 的长逐渐减少 C、线段 的长保持不变 D、线段 的长先增大后减小8. 如图 是正五边形 的三个外角,若 则 =( )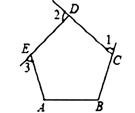 A、 B、 C、 D、9.
A、 B、 C、 D、9.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形.该小正方形的序号是( )
 A、① B、② C、③ D、④10. 关于 的分式方程 有增根,则 的值是( )A、1 B、2 C、4 D、1或411. 如图,平行四边形ABCD中,∠B=60°,AB⊥AC,AC的垂直平分线交AD于点E,△CDE的周长是15,则平行四边形ABCD的面积为( )
A、① B、② C、③ D、④10. 关于 的分式方程 有增根,则 的值是( )A、1 B、2 C、4 D、1或411. 如图,平行四边形ABCD中,∠B=60°,AB⊥AC,AC的垂直平分线交AD于点E,△CDE的周长是15,则平行四边形ABCD的面积为( )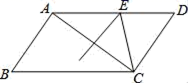 A、 B、40 C、50 D、12. 如图所示,在平面直角坐标系中,将边长为1的正方形 绕点 顺时针旋转45°后得到正方形 .依此方式,绕点 连续旋转2021次得到正方形 ,那么点 的坐标是( )
A、 B、40 C、50 D、12. 如图所示,在平面直角坐标系中,将边长为1的正方形 绕点 顺时针旋转45°后得到正方形 .依此方式,绕点 连续旋转2021次得到正方形 ,那么点 的坐标是( )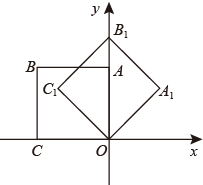 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 代数式 有意义,则x的取值范围是.14. 把 分解因式,结果为 .15. 如图,平行四边形 中, 平分 交 于点 , 平分 交 于点 .若 , ,则 的长为 .
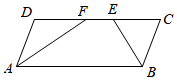 16. 现规定一种新运算, ,其中 、 为常数.已知关于 的不等式 的解集在数轴上表示如图,则 的值为 .
16. 现规定一种新运算, ,其中 、 为常数.已知关于 的不等式 的解集在数轴上表示如图,则 的值为 . 17.
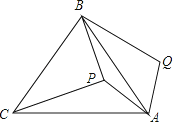
17.如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为 .
 18. 如图,在四边形 中, , , , 是 的中点.点 以每秒1个单位长度的速度从点 出发,沿 向点 运动;点 同时以每秒2个单位长度的速度从点 出发,沿 向点 运动.点 停止运动时,点 也随之停止运动,当运动时间 时,以点 , , , 为顶点的四边形是平行四边形.
18. 如图,在四边形 中, , , , 是 的中点.点 以每秒1个单位长度的速度从点 出发,沿 向点 运动;点 同时以每秒2个单位长度的速度从点 出发,沿 向点 运动.点 停止运动时,点 也随之停止运动,当运动时间 时,以点 , , , 为顶点的四边形是平行四边形.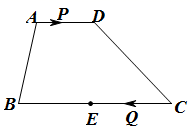
三、解答题
-
19. 例:解不等式(x﹣2)(x+3)>0
解:由实数的运算法则:“两数相乘,同号得正”
得① ,或② ,
解不等式组①得,x>2,
解不等式组②得,x<﹣3,
所以原不等式的解集为x>2或x<﹣3.
阅读例题,尝试解决下列问题:
(1)、平行运用:解不等式x2﹣9>0;(2)、类比运用:若分式 的值为负数,求x的取值范围.20. 已知某正多边形的一个内角比它相邻外角的3倍还多20°.(1)、求这个正多边形一个内角的度数;(2)、求这个正多边形的内角和.21. 先化简,再求值 ,其中 是不等式组 的整数解.22. 如图,平行四边形 对角线 、 相交点 , 、 是平行四边形 的对角线 上的两点,且 , ,连接 、 、 、 .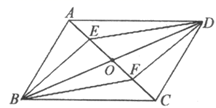 (1)、求证:四边形 为平行四边形;(2)、若 , ,求 的长.23. 为打赢“扶贫攻坚战”,某单位计划选购甲、乙两种果树苗送给贫困户,已知甲种果树苗单价比乙种果树苗的单价高10元,若用500元单独购买甲种果树苗与300元单独购买乙种果树苗的数量相同.(1)、请问甲,乙两种果树苗的单价各为多少元?(2)、如果该单位计划购买甲,乙两种水果树苗共5500棵,总费用不超过92500元,则甲种果树苗最多可以购买多少棵?24. 整式乘法与多项式因式分解是既有联系又有区别的两种变形.
(1)、求证:四边形 为平行四边形;(2)、若 , ,求 的长.23. 为打赢“扶贫攻坚战”,某单位计划选购甲、乙两种果树苗送给贫困户,已知甲种果树苗单价比乙种果树苗的单价高10元,若用500元单独购买甲种果树苗与300元单独购买乙种果树苗的数量相同.(1)、请问甲,乙两种果树苗的单价各为多少元?(2)、如果该单位计划购买甲,乙两种水果树苗共5500棵,总费用不超过92500元,则甲种果树苗最多可以购买多少棵?24. 整式乘法与多项式因式分解是既有联系又有区别的两种变形.例如, 是单项式乘多项式的法则;把这个法则反过来,得到 ,这是运用提取公因式法把多项式因式分解.
又如 、 是多项式的乘法公式;把这些公式反过来,得到 、 ,这是运用公式法把多项式因式分解.
有时在进行因式分解时,以上方法不能直接运用,观察甲、乙两名同学的进行的因式分解.
甲:
(分成两组)
(分别提公因式)
乙:
(分成两组)
(运用公式)
请你在他们解法的启发下,完成下面的因式分解
问题一:因式分解:
(1)、 ;(2)、 .(3)、问题二:探究对 、 定义一种新运算 ,规定: (其中 , 均为非零常数).当 时, 对任意有理数 、 都成立,试探究 , 的数量关系.
25. 如图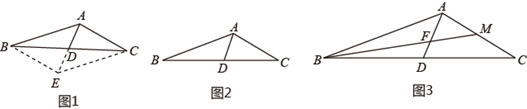 (1)、如图1所示,在 中, 为 的中点,求证:
(1)、如图1所示,在 中, 为 的中点,求证:甲说:不可能出现 ,所以此题无法解决;
乙说:根据倍长中线法,结合我们新学的平行四边形的性质和判定,我们可延长 至点 ,使得 ,连接 、 ,由于 ,所以可得四边形 是平行四边形,请写出此处的依据(平行四边形判定的文字描述)
所以 , 中, ,
即
(2)、如图2,在 中, 为 的中点, , , ,求 的面积;(3)、如图3,在 中, 为 的中点, 为 的中点,连接 交 于 ,若 .求证: .