山东省青岛市市南区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是中心对称图形不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ，下列选项中，能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $A D = A B$ ， $B C = C D$ B、 $A D / / B C$ ， $A B = C D$ C、 $A D = B C$ ， $A D / / B C$ D、 $A O = B O$ ， $C O = D O$

查看试题解析
3. 不等式 $x + 2 < 3 x + 6$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
4. 若把分式 $\frac{x + 2 y}{5 x y}$ 中的 $x$ 、 $y$ 都缩小为原来的一半，则分式的值（）

A、缩小为原来的四分之一 B、缩小为原来的一半 C、不变 D、扩大为原来的 $2$ 倍

查看试题解析
5. 如图， $△ A B C$ 中， $∠ A = 90 °$ ，点 $M$ 、 $N$ 分别为边 $A B$ 和 $A C$ 的中点，若 $A B = 2$ ， $A C = 4$ ，则 $M N$ 的长度为（）

A、 $2 \sqrt{3}$ B、 $\sqrt{3}$ C、 $2 \sqrt{5}$ D、 $\sqrt{5}$

查看试题解析
6. 已知分式方程 $\frac{x - 5}{2 x - 6} = \frac{m}{x - 3}$ 有增根，则m的值是（）

A、-1 B、5 C、1 D、3

查看试题解析
7. 已知平行四边形 $A B C D$ 周长为 $26 cm$ ，对角线 $A C$ 、 $B D$ 相交于点 $O$ ，已知 $△ B O C$ 的周长比 $△ A O B$ 的周长多 $3 cm$ ，则 $B C$ 的长度为（）

A、 $5 cm$ B、 $6 cm$ C、 $7 cm$ D、 $8 cm$

查看试题解析
8. 如图，函数 $y_{1} = \frac{1}{2} x$ 与 $y_{2} = a x + 5$ 图象交于点 $A (m ， 2)$ ，则关于 $x$ 的不等式 $\frac{1}{2} x \leq a x + 5$ 的解集是（）

A、 $x \leq 4$ B、 $x \geq 4$ C、 $x \leq 2$ D、 $x \geq 2$

查看试题解析

二、填空题

9. 因式分解： $8 x^{2} - 2 =$ ．

查看试题解析
10. 如图， $R t △ A B C$ 中， $∠ A = 90 °$ ， $∠ B = 30 °$ ，边 $B C$ 的中垂线分别交 $B C$ 、 $A B$ 于点 $D$ 、点 $E$ ，若 $D E = 1 cm$ ，则 $△ A B C$ 的周长为 $cm$ ．

查看试题解析
11. 某工程队进行爆破时，为了安全，人要撤离到距爆破点 $50$ 米以外的安全区域．已知引线的燃烧速度为 $0.2$ 米/秒，爆破者离开速度为 $3$ 米/秒，点燃时引线向远离爆破点的方向拉直，则引线的长度应满足什么条件？设引线长 $x$ 米，请根据题意列出关于 $x$ 的不等式．

查看试题解析
12. 某装修公司拟用三种边长相同的正多边形地砖无缝隙、无重叠的铺满整个客厅，如图所示，已知点 $A$ 周围有三块地砖，则第三块地砖的边数为．

查看试题解析
13. 在平行四边形 $A B C D$ 中， $A D = 10 cm$ ， $A E$ 平分 $∠ B A D$ 交 $B C$ 于点 $E$ ， $D F$ 平分 $∠ A D C$ 交 $B C$ 于点 $F$ ，且 $E F = 4 cm$ ，则 $A B =$ $cm$ ．

查看试题解析
14. 如图， $△ A B C$ 是边长为 $2$ 的等边三角形，点 $B$ 、点 $C$ 的坐标分别为 $(- 1 ， 0)$ 、 $(1 ， 0)$ ．第一次将 $△ A B C$ 绕点 $O$ 顺时针旋转 $60 °$ 得到 $△ A_{1} B_{1} C_{1}$ （点 $A$ 、 $B$ 、 $C$ 的对应点分别是点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ ，以此类推），第二次仍将 $△ A_{1} B_{1} C_{1}$ 绕点 $O$ 顺时针旋转 $60 °$ 得到 $△ A_{2} B_{2} C_{2}$ ，……，按此方法进行下去，则点 $A_{2021}$ 的坐标为．

查看试题解析

三、解答题

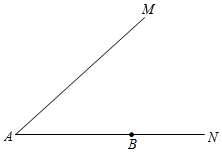
15. 如图，已知点 $B$ 是 $∠ M A N$ 边 $A N$ 上一点．求作：平行四边形 $A B C D$ ，使点 $D$ 在射线 $A M$ 上，且 $∠ A B D = 90 °$ ．

查看试题解析
16.

(1)、化简： $\frac{x^{2}}{x + 1} - x + 1$

(2)、解方程： $\frac{8}{x - 2} - 3 = \frac{7 - 4 x}{2 - x}$

查看试题解析
17.

(1)、解不等式组 ${\begin{array}{l} \frac{2 x - 1}{3} - \frac{5 x + 1}{2} \leq 1 \\ 5 x - 1 < 3 (x + 1) \end{array}$ ，并写出它的非负整数解．

(2)、先化简，再求值： $(\frac{x^{2}}{x - 1} - \frac{2 x + 1}{1 - x}) \div \frac{x + 1}{x - 1}$ ，并从 $- 1$ ， $0$ ， $1$ ， $2$ 四个数中选一个合适的数代入求值．

查看试题解析
18. 某儿童游乐中心设置两种收费方式：普通消费每次收费 $30$ 元；会员消费每月交 $120$ 元会员费，可以免费游玩 $2$ 次，超过 $2$ 次后每次按普通消费打六折收费．小明每个月去此游乐中心多少次时选择会员消费合算？

查看试题解析
19. 为庆祝建党100周年，学校组织学生前往距学校132千米的某革命根据地参观学习．一班先乘车前往，二班所乘汽车因事耽搁，50分钟后二班再乘车出发，为了赶上一班，平均车速是一班平均车速的1.2倍，结果还是比一班晚到20分钟．求一班的平均车速是多少千米/时？

查看试题解析
20. 如图

(1)、如图1，现有编号为①②③④的四种长方体各若干块，现取其中两块拼成一个大长方体如图2，据此写出一个多项式的因式分解：．

(2)、若要用这四种长方体拼成一个棱长为 $(x + 1)$ 的正方体，需要②号长方体个，③号长方体个，据此写出一个多项式的因式分解：．

查看试题解析
21. 已知：如图，在 $△ A B C$ 中， $A B = A C$ ， $B D ⊥ A C$ 于点 $D$ ， $C E ⊥ A B$ 于点 $E$ ，过点 $D$ 作 $C E$ 的平行线交 $B C$ 延长线于点 $F$ ，连接 $D E$ ．求证：

(1)、 $∠ D B C = ∠ E C B$ ；

(2)、 $D E = C F$ ．

查看试题解析
22. 某餐厅推出健康套餐，一份套餐 $A$ 含鸡肉0.05千克，牛肉0.1千克，这两种肉类的成本共11元；一份套餐 $B$ 含鸡肉0.1千克，牛肉0.05千克，这两种肉类的成本共7元．

(1)、每千克鸡肉和牛肉成本各多少元？

(2)、若每千克鸡肉含胆固醇11个单位，每千克牛肉含胆固醇6个单位，一份健康套餐的胆固醇含量不得超过1个单位，现用鸡肉、牛肉这两种肉类共0.15千克制作一份健康套餐，则这份套餐的肉类成本最低是多少元？

查看试题解析
23. 如图

如图 $1$ ，线段 $A B$ 绕端点 $B$ 顺时针旋转 $x °$ ，得到线段 $A^{'} B$ ，此时线段 $A B$ 与线段 $A^{'} B$ 的夹角 $∠ A B A^{'} = x °$ ；

(1)、将线段 $M N$ 绕点 $O$ 顺时针旋转 $x ° (0 < x < 180)$ ，得到线段 $M^{'} N^{'}$ ，
①如图 $2$ ，两条线段相交于点 $P$ ，那么线段 $M N$ 与线段 $M^{'} N^{'}$ 的夹角 $∠ N P N^{'}$ 是多少度？请写出推导过程．

②如图 $3$ ，当线段 $M N$ 与线段 $M^{'} N^{'}$ 的位置如图所示时，这两条线段所在直线的夹角（小于或等于 $90 °$ 的角）是多少度？请写出推导过程．

③由以上探究可得结论：一个图形绕某点旋转 $x °$ 后，对应线段或对应线段所在直线的夹角（小于或等于 $90 °$ 的角）为 ▲ 度．

(2)、如图 $4$ ，点 $E$ 是正方形 $A B C D$ 内一点， $∠ B C E = 30 °$ ， $B E = 1$ ， $C E = \sqrt{2}$ ，将 $△ B C E$ 绕点 $B$ 逆时针旋转 $90 °$ ，得到 $△ B A E^{'}$ ，连接 $E E^{'}$ ，延长 $C E$ 交 $A E^{'}$ 于点 $F$ ，则以下结论：① $C E ⊥ A E^{'}$ ；②点 $F$ 为 $A E^{'}$ 的中点；③ $△ A E E^{'}$ 为等边三角形；④ $A B = \frac{\sqrt{2}}{2} + \frac{\sqrt{3}}{2}$ 正确的是（只填序号）．

查看试题解析
24. 如图， $△ A B C$ 中， $∠ A = 90 °$ ， $A B = A C = 5 cm$ ，点 $P$ 是 $A C$ 边上一动点，以 $1 cm / s$ 的速度由 $A$ 向 $C$ 运动，同时点 $Q$ 从点 $B$ 出发，在 $C B$ 延长线上，以 $\sqrt{2} cm / s$ 的速度向左运动，运动时间为 $t$ 秒，当点 $P$ 到达点 $C$ 时，两点停止运动．连接 $P Q$ 交 $A B$ 于点 $D$ ，过点 $P$ 作 $P E ⊥ B C$ 于 $E$ ，过点 $Q$ 作 $B C$ 的垂线交 $A B$ 延长线于 $F$ ，连接 $E F$ ．

(1)、用含 $t$ 的代数式表示线段长度： $P C =$ ， $P E =$ ；

(2)、当 $t$ 取何值时，四边形 $P Q F E$ 是平行四边形？请写出推理过程．

(3)、在运动过程中，点 $D$ 是否总是 $P Q$ 的中点？请说明理由．

(4)、是否存在某一时刻 $t$ ，使得 $△ B D Q$ 是等腰三角形？若存在，求出 $t$ 的值；若不存在，请说明理由．

查看试题解析