山东省青岛市李沧区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-09 类型:期末考试
一、单选题
-
1. 实数a与b在数轴上的位置如图所示,则下列各式正确的是( )
 A、 B、 C、 D、2. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
A、 B、 C、 D、2. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 下面的计算过程中,从哪一步开始出现错误( )A、① B、② C、③ D、④4. 的顶点分别位于格点,建立如图所示平面直角坐标系,将 绕点B按顺时针方向旋转90°,再向下平移2个单位长度,得到 ,则点A的对应点 的坐标是( )
3. 下面的计算过程中,从哪一步开始出现错误( )A、① B、② C、③ D、④4. 的顶点分别位于格点,建立如图所示平面直角坐标系,将 绕点B按顺时针方向旋转90°,再向下平移2个单位长度,得到 ,则点A的对应点 的坐标是( )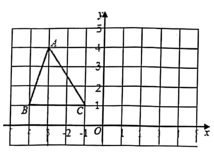 A、 B、 C、 D、5. 如果平行四边形的一边长是10,那么这个平行四边形的两条对角线的长度可以是( )A、4和6 B、6和8 C、20和30 D、8和126. 下列分解因式正确的是( )A、 B、 C、 D、7. 如图, 中, , 平分 , 于点 , 于点 , ,则 的长为( )
A、 B、 C、 D、5. 如果平行四边形的一边长是10,那么这个平行四边形的两条对角线的长度可以是( )A、4和6 B、6和8 C、20和30 D、8和126. 下列分解因式正确的是( )A、 B、 C、 D、7. 如图, 中, , 平分 , 于点 , 于点 , ,则 的长为( )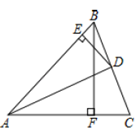 A、3 B、4 C、5 D、68. 如图,已知直线 过点 ,过点 的直线 交 轴于点 ,则关于的不等式组 的解集为( )
A、3 B、4 C、5 D、68. 如图,已知直线 过点 ,过点 的直线 交 轴于点 ,则关于的不等式组 的解集为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
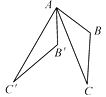
9. 若一个正多边形的每一个外角都等于相邻内角的 ,则这个多边形的内角和为度.10. 如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为 .
 11. 若分式方程 有增根,则a= .12. 如图,在 中,DE垂直平分BC交AB于点E , 若 , 的周长为31,则 的周长为 .
11. 若分式方程 有增根,则a= .12. 如图,在 中,DE垂直平分BC交AB于点E , 若 , 的周长为31,则 的周长为 .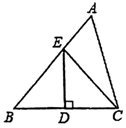 13. 用三块正多边形的木板铺地,拼在一起的三块正多边形木板顶点重合,且各边完全吻合,其中两块木板的边数分别是4和6,则第三块木板的边数是 .14. 如图, 中, , , ,将 沿射线BC的方向平移,得到 ,再将 绕点 逆时针旋转一定角度后,点 恰好与点C重合,则 平移的距离为 .
13. 用三块正多边形的木板铺地,拼在一起的三块正多边形木板顶点重合,且各边完全吻合,其中两块木板的边数分别是4和6,则第三块木板的边数是 .14. 如图, 中, , , ,将 沿射线BC的方向平移,得到 ,再将 绕点 逆时针旋转一定角度后,点 恰好与点C重合,则 平移的距离为 . 15. 在平面直角坐标系中,点A , B , C的坐标分别是(0,0),(5,0),(2,3),以点A、B、C和点D为顶点构造平行四边形,则点D的坐标是.16. 如图,图①是一个三角形,分别连接这个三角形三边中点得到第2个图形(图②),再连接图②中间小三角形三边的中点得到第3个图形(图③),…,依此规律进行下去,则第 个图形中有个平行四边形.
15. 在平面直角坐标系中,点A , B , C的坐标分别是(0,0),(5,0),(2,3),以点A、B、C和点D为顶点构造平行四边形,则点D的坐标是.16. 如图,图①是一个三角形,分别连接这个三角形三边中点得到第2个图形(图②),再连接图②中间小三角形三边的中点得到第3个图形(图③),…,依此规律进行下去,则第 个图形中有个平行四边形.


三、解答题
-
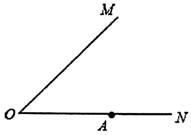
17. 已知:如图,∠MON及边ON上一点A .
求作:在 内部的点P , 使得 ,且点P到 两边的距离相等.
 18. 分解因式:(1)、(2)、19. 计算题:(1)、解不等式组:(2)、化简:(3)、解方程:20. 已知:如图, 是 平分线上的一点, , ,垂足分别为 , ,连接 .
18. 分解因式:(1)、(2)、19. 计算题:(1)、解不等式组:(2)、化简:(3)、解方程:20. 已知:如图, 是 平分线上的一点, , ,垂足分别为 , ,连接 .
求证:
(1)、 ;(2)、 是 的垂直平分线.21. 某厂原计划在规定时间内生产通讯设备60台,由于改进了操作技术,每天生产的台数比原计划多50%,结果提前两天完成任务.求改进操作技术后每天生产通讯设备多少台.22. 如图,四边形ABCD是平行四边形,E , F是对角线BD上的点, .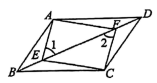 (1)、求证:(2)、线段AF与CE有什么关系?请证明你的结论.23. 某体育用品商店购进A、B两种不同品牌的足球,购进A品牌足球的总费用为2000元,购买B品牌足球的总费用为1400元,已知购买A品牌足球的数量比B品牌的数量多20个,且B品牌足球的购进单价是A品牌单价的1.4倍.(1)、求A , B两种品牌足球的购进单价各是多少元;(2)、若计划用不超过4500元的资金再次购进A , B两种品牌的足球共80个,已知A , B两种品牌足球的进价不变,若A品牌足球每个的售价为60元,而B品牌足球每个售价为88元,问:如何购进两种品牌的足球,才能使卖完这批足球后的利润最大,最大利润是多少?24. 如图,在四边形ABCD中, , ,∠BAD=45°,BC=8,DC=6,动点P沿射线DA的方向以每秒2个单位长度的速度运动,动点Q在线段CB上以每秒1个单位长度的速度向点B运动,点P、Q分别从点D、C同时出发,设运动的时间为t(秒)
(1)、求证:(2)、线段AF与CE有什么关系?请证明你的结论.23. 某体育用品商店购进A、B两种不同品牌的足球,购进A品牌足球的总费用为2000元,购买B品牌足球的总费用为1400元,已知购买A品牌足球的数量比B品牌的数量多20个,且B品牌足球的购进单价是A品牌单价的1.4倍.(1)、求A , B两种品牌足球的购进单价各是多少元;(2)、若计划用不超过4500元的资金再次购进A , B两种品牌的足球共80个,已知A , B两种品牌足球的进价不变,若A品牌足球每个的售价为60元,而B品牌足球每个售价为88元,问:如何购进两种品牌的足球,才能使卖完这批足球后的利润最大,最大利润是多少?24. 如图,在四边形ABCD中, , ,∠BAD=45°,BC=8,DC=6,动点P沿射线DA的方向以每秒2个单位长度的速度运动,动点Q在线段CB上以每秒1个单位长度的速度向点B运动,点P、Q分别从点D、C同时出发,设运动的时间为t(秒)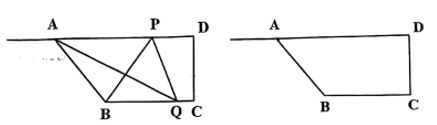 (1)、 时,是否存在某一时刻t , 使得 与 面积之比为2:3?若存在,求t的值;若不存在,请说明理由;(2)、当t为何值时,点P在∠ABC的角平分线上?请说明理由;(3)、设AQ中点为E , 连接BD , 与PQ相交于点F , 若EF是 的中位线,求此时点E到PQ的距离.
(1)、 时,是否存在某一时刻t , 使得 与 面积之比为2:3?若存在,求t的值;若不存在,请说明理由;(2)、当t为何值时,点P在∠ABC的角平分线上?请说明理由;(3)、设AQ中点为E , 连接BD , 与PQ相交于点F , 若EF是 的中位线,求此时点E到PQ的距离.