山东省济宁市兖州区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-09 类型:期末考试
一、单选题
-
1. 下列各曲线中,不表示 是 的函数的是( )A、
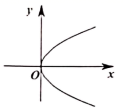 B、
B、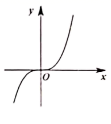 C、
C、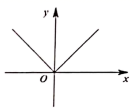 D、
D、 2. 某男装专卖店老板专营某品牌夹克,店主统计了一周中不同尺码的夹克销售量如下表:如果每件夹克的利润相同,你认为该店主最关注的销售数据是下列统计量中的( )
2. 某男装专卖店老板专营某品牌夹克,店主统计了一周中不同尺码的夹克销售量如下表:如果每件夹克的利润相同,你认为该店主最关注的销售数据是下列统计量中的( )尺码
39
40
41
42
43
平均每天销售量/件
10
12
20
12
12
A、平均数 B、方差 C、众数 D、中位数3. 一次函数 的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列运算,结果正确的是( )A、 B、 C、 D、5. 如图,在四边形ABCD中,对角线AC和BD相交于点O , 下列条件不能判断四边形ABCD是平行四边形的是( )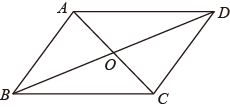 A、 , B、 , C、 , D、 ,6. 顺次连接矩形四边中点所得的四边形一定是()A、正方形 B、矩形 C、菱形 D、等腰梯形7. 如图,2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么 的值为( )
A、 , B、 , C、 , D、 ,6. 顺次连接矩形四边中点所得的四边形一定是()A、正方形 B、矩形 C、菱形 D、等腰梯形7. 如图,2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么 的值为( )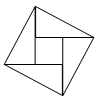 A、13 B、19 C、25 D、1698. 将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )
A、13 B、19 C、25 D、1698. 将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )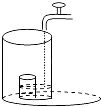 A、
A、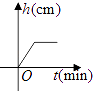 B、
B、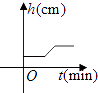 C、
C、 D、
D、 9. 如图1,在平面直角坐标系中, 在第一象限,且 轴.直线 从原点 出发沿x轴正方向平移.在平移过程中,直线被 截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示.那么 的面积为( )
9. 如图1,在平面直角坐标系中, 在第一象限,且 轴.直线 从原点 出发沿x轴正方向平移.在平移过程中,直线被 截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示.那么 的面积为( )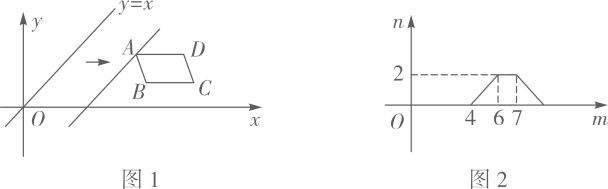 A、3 B、 C、6 D、10. 如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是( )
A、3 B、 C、6 D、10. 如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是( )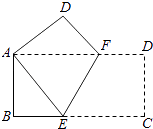 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 试写出一组勾股数 .12. 若二次根式 在实数范围内有意义,则x的取值范围是 .
13. 如图是甲、乙两名射由运动员的10次射击训练成绩的折线统计图观察图形,比较甲、乙这10次射击成绩的方差S甲2、S乙2的大小:S甲2S乙2(填“>”、“<”或“=”)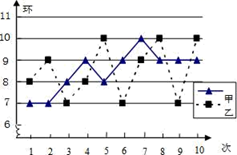 14. 如图,等腰 的底边BC=20,面积为120,点D在BC边上,且CD=5,直线EF是腰AC的垂直平分线,若点M在EF上运动,则∆CDM周长的最小值为 .
14. 如图,等腰 的底边BC=20,面积为120,点D在BC边上,且CD=5,直线EF是腰AC的垂直平分线,若点M在EF上运动,则∆CDM周长的最小值为 .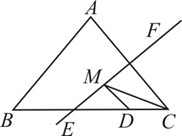 15. 在平而直角坐标系中,直线 与y轴交于点A , 如图所示,依次作正方形 ,正方形 ,正方形 ,正方形 ,……点 , , , ……在直线l上,点 , , , ……在x轴正半轴上,则前n个正方形对角线长的和是 .
15. 在平而直角坐标系中,直线 与y轴交于点A , 如图所示,依次作正方形 ,正方形 ,正方形 ,正方形 ,……点 , , , ……在直线l上,点 , , , ……在x轴正半轴上,则前n个正方形对角线长的和是 .
三、解答题
-
16. 计算:17. 如图,已知 , , , , .
 (1)、求AC的长.(2)、求图中阴影部分图形的面积.18. 下表某公司25名员工月收入的资料.
(1)、求AC的长.(2)、求图中阴影部分图形的面积.18. 下表某公司25名员工月收入的资料.月收入/元
45000
17000
10000
5600
5000
3800
3000
1600
人数
1
1
1
4
5
1
11
1
(1)、这个公司员工月收入的平均数是6312,中位数是 , 众数是;(2)、在(1)中三个集中趋势参数中,你认为用哪一个反映公司全体员工月收入水平更合适?请说明理由.19. 已如一次函数y=kx+b的图象经过点(-1.-5),且与正比例函数y= x的图象相交于点(2,a),求: (1)、a的值:(2)、k,b的值;(3)、在同一平面直角坐标系中画出这两个函数的图象;(4)、求这两个函数图象与x轴所围成的三角形的面积.20. 已知:如图,在边长为1的正方形ABCD中,点P是对角线AC上的一个动点(与点A、C不重合),过点P作 ,PE交边CD于点E , 过点E作 ,垂足为F .
(1)、a的值:(2)、k,b的值;(3)、在同一平面直角坐标系中画出这两个函数的图象;(4)、求这两个函数图象与x轴所围成的三角形的面积.20. 已知:如图,在边长为1的正方形ABCD中,点P是对角线AC上的一个动点(与点A、C不重合),过点P作 ,PE交边CD于点E , 过点E作 ,垂足为F .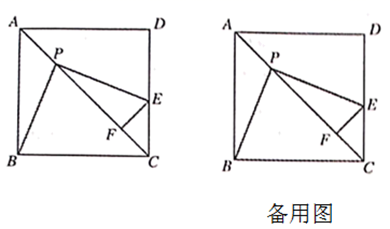 (1)、求证: ;(2)、在点P的运动过程中,PF的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程;若变化,试说明理由.21. 某商店计划采购甲、乙两种不同型号的平板电脑共20台,已知甲型平板电脑进价1600元,售价2000元;乙型平板电脑进价为2500元,售价3000元.(1)、设该商店购进甲型平板电脑x台,请写出全部售出后该商店获利y与x之间函数表达式.(2)、若该商店采购两种平板电脑的总费用不超过39200元,全部售出所获利润不低于8500元,请设计出所有采购方案,并求出使商店获得最大利润的采购方案及最大利润.22. 综合与实践
(1)、求证: ;(2)、在点P的运动过程中,PF的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程;若变化,试说明理由.21. 某商店计划采购甲、乙两种不同型号的平板电脑共20台,已知甲型平板电脑进价1600元,售价2000元;乙型平板电脑进价为2500元,售价3000元.(1)、设该商店购进甲型平板电脑x台,请写出全部售出后该商店获利y与x之间函数表达式.(2)、若该商店采购两种平板电脑的总费用不超过39200元,全部售出所获利润不低于8500元,请设计出所有采购方案,并求出使商店获得最大利润的采购方案及最大利润.22. 综合与实践在线上教学中,教师和学生都学习到了新知识,掌握了许多新技能.例如教材八年级下册的数学活动一一折纸,就引起了许多同学的兴趣.在经历图形变换的过程中,进一步发展了同学们的空间观念,积累了数学活动经验.
 (1)、实践发现:
(1)、实践发现:对折矩形纸片ABCD , 使AD与BC重合,得到折痕EF , 把纸片展平;再一次折叠;纸片,使点A落在EF上的点N处,并使折痕经过点B , 得到折痕BM , 把纸片展平,连接AN , 如图①.
折痕BM(填“是”或“不是”)线段AN的垂直平分线;请判断图中 是什么特殊三角形?答:;进一步计算出 ;
(2)、继续折叠纸片,使点A落在BC边上的点H处,并使折痕经过点B , 得到折痕BG , 把纸片展平,如图②,则 ;(3)、拓展延伸:如图③,折叠矩形纸片ABCD , 使点A落在BC边上的点 处,并且折痕交BC边于点T , 交AD边于点S , 把纸片展平,连接 交ST于点O , 连接AT , .
求证:四边形 是菱形.
(4)、解决问题:如图④,矩形纸片ABCD中, , ,点S是边AD上的一动点,折叠纸片,使点A落在BC边上的点 处,并且折痕过点S , 交AB边于点T , 把纸片展平.同学们小组讨论后,得出线段AT长度的取值范围,请你求出线段AT长度的取值范围.