山东省济南市章丘区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-09 类型：期末考试

进入出卷网下载

一、单选题

1. 如图所示图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若 $a > b$ ，则下列各式中一定成立的是（）

A、 $a - 2 < b - 2$ B、 $a c^{2} > b c^{2}$ C、 $- 2 a > - 2 b$ D、 $a + 2 > b + 2$

查看试题解析
3. 下列从左到右的变形中，是因式分解的是（）

A、x²＋2x＋3＝（x＋1）²＋2 B、15x²y＝3x·5xy C、2（x＋y）＝2x＋2y D、x²＋6x＋9＝（x＋3）²

查看试题解析
4. 分式 $\frac{2}{2 - x}$ 可变形为（）

A、 $\frac{2}{2 + x}$ B、 $- \frac{2}{2 + x}$ C、 $\frac{2}{x - 2}$ D、 $- \frac{2}{x - 2}$

查看试题解析
5. 已知不等式组 ${\begin{array}{l} x \geq a \\ - 3 x > - 6 \end{array}$ 有解，则a的取值范围是（）

A、a≥2 B、a≤2 C、a＞2 D、a＜2

查看试题解析
6. 能判定四边形ABCD是平行四边形的是（）

A、AB∥CD，AB＝CD B、AB＝BC，AD＝CD C、AC＝BD，AB＝CD D、AB∥CD，AD＝CB

查看试题解析
7. 如图，在Rt△ABC中，∠B＝90°，ED是AC的垂直平分线，交AC于点D ，交BC于点E ．已知∠BAC＝5∠BAE ，则∠C的度数为（）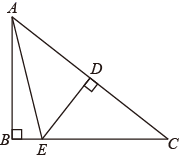

A、30° B、40° C、50° D、60°

查看试题解析
8. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A'B'C ，连接AA'，若∠1=25°，则∠BAA'的度数是(　　)

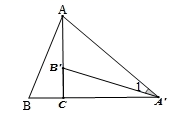A、70° B、65° C、60° D、55°

查看试题解析
9. 若9x²+2(k-3)x+16是完全平方式，则k的值为（）

A、15 B、15 或－15 C、39 或－33 D、15 或－9

查看试题解析
10. 已知a＋b＝3，ab＝1，则多项式a²b＋ab²的值为（）

A、1 B、3 C、4 D、6

查看试题解析
11. 如图，将△ABC放在每个小正方形边长均为1的网格中，点A、B、C均落在格点上，若点B的坐标为（2，﹣1），则到△ABC三个顶点距离相等的点的坐标为（）

A、（0，1） B、（3，1） C、（1，﹣1） D、（0，0）

查看试题解析
12. 已知等边△ABC的边长为4，点P是边BC上的动点，将△ABP绕点A逆时针旋转60°得到△ACQ ，点D是AC边的中点，连接DQ ，则DQ的最小值是（）

A、 $\sqrt{2}$ B、 $\sqrt{5}$ C、2 D、 $\sqrt{3}$

查看试题解析

二、填空题

13. 分解因式：a²-9= ．

查看试题解析
14. 若分式 $\frac{x^{2} - 1}{x - 1}$ 的值为0，则x的值为.

查看试题解析
15. 如图，平行四边形ABCD的周长为36cm，对角线AC、BD相交于点O ， AC＝12cm．若点E是AB的中点，则△AOE的周长为；

查看试题解析
16. 如图，已知函数 $y = 3 x + b$ 和 $y = a x - 3$ 的图象交于点 $P (- 2 ， - 5)$ ，则根据图象可得不等式 $3 x + b > a x - 3$ 的解集是．

查看试题解析
17. 如图，在△ABC中，BF平分∠ABC ， AF⊥BF于点F ， D为AB的中点，连接DF延长交AC于点E ．若AB＝20，BC＝32，则线段EF的长为；

查看试题解析
18. 如图，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，四边形ACDE是平行四边形，连接CE交AD于点F ，连接BD交CE于点G ，连接BE ．下列结论中： ①CE＝DB；②△ADC是等腰直角三角形；③∠ADB＝∠AEB；④CD＝EF；⑤S_{四边形BCDE}＝ $\frac{1}{2}$ BD·CE；⑥BC²＋DE²＝BE²＋CD²；其中一定正确的是（把所有正确结论的序号填在模线上）

查看试题解析

三、解答题

19. 解不等式组： ${\begin{array}{l} 3 x - (x - 2) \geq 4 \\ \frac{2 x + 1}{3} > x - 1 \end{array}$ ，并写出不等式组的所有整数解．

查看试题解析
20. 因式分解：

(1)、a³b－2a²b²＋ab³

(2)、（x²＋4）²－16x² ．

查看试题解析
21. 如图，在△ABC中，D是BC边上的中点，F、E分别是AD及其延长线上的点，CF//BE ．请连接BF、CE ，试判断四边形BECF是何种特殊四边形，并说明理由．

查看试题解析
22.

(1)、化简 $(\frac{1}{x - 1} - \frac{1}{x + 1}) \div \frac{x}{2 x^{2} - 2}$

(2)、解方程： $\frac{x - 1}{4 - x} = 2 - \frac{3}{x - 4}$

查看试题解析
23. 在边长为1个单位长度的小正方形组成的网格中，建立平面直角坐标系，△ABC的位置如图所示，先作△ABC关于原点O成中心对称的△A₁B₁C₁ ，再把△A₁B₁C₁向上平移4个单位长度得到△A₂B₂C₂ ．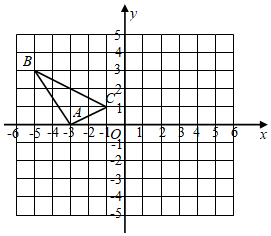

(1)、画出△A₁B₁C₁和△A₂B₂C₂ ．

(2)、△A₂B₂C₂与△ABC关于某点成中心对称，直接写出对称中心的坐标；

(3)、已知P为x轴上一点．若△ABP的面积为3，直接写出点P的坐标；

查看试题解析
24. 疫情期间，为满足市民的防护需求，某医药公司想要购买A、B两种口罩，在进行市场调研时发现：A型口罩比B型口罩每包进价多了10元，用68000元购买A型口罩的包数是用32000元购买B型口罩包数的2倍．

(1)、A、B型口罩进价分别为每包多少元?

(2)、若该公司计划购买A、B型口罩共200包，其中A型口罩的包数不大于B型口罩的包数，且用于购买A型口罩的钱数多于购买B型口罩的钱数．设购买A型口罩x包，则符合条件的进货方案共多少种?（包数均为整数，不用列出方案）

(3)、在（2）的条件下，已知该公司A型口罩的售价为240元/包，B型口罩的售价为220元/包．假设所有口罩均能全部售出，请求出采用哪种方案时，该公司获得的收益最大?最大收益为多少?

查看试题解析
25. 如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝1，将三角板中30°角的顶点D放在AB边上移动，使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F ，且使DE始终与AB垂直．

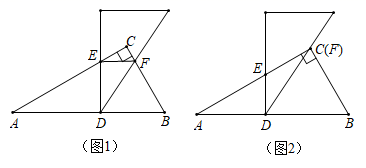(1)、如图1，求证：△BDF是等边三角形；

(2)、如图2，当DF通过点C（即点F与点C重合时），求DE的长；

(3)、若移动点D当EF//AB时，求AD的长．

查看试题解析
26. 已知Rt△ABC中，∠ACB＝90°，CA＝CB＝4，另有一块等腰直角三角板的直角顶点放在C处，CP＝CQ＝2，将三角板CPQ绕点C旋转（保持点P在△ABC内部），连接AP、BP、BQ ．

(1)、如图1，求证：AP＝BQ；

(2)、如图2，当PQ⊥BQ时，求AP的长；

(3)、如田3，设射线AP与射线BQ相交于点E ，连接EC ，写出旋转过程中EP、EQ、EC之间的数量关系，并简述理由．

查看试题解析
27. 如图，在平面直角坐标系xOy中，直线y＝－ $\frac{1}{2}$ x＋ $\frac{3}{2}$ 与y＝x相交于点A ，与x轴交于点B ．

(1)、求点A ， B的坐标；

(2)、在平面直角坐标系xOy中，是否存在一点C ，使得以O ， A ， B ， C为顶点的四边形是平行四边形？如果存在，试求出所有符合条件的点C的坐标；如果不存在，请说明理由；

(3)、在直线OA上，是否存在一点D ，使得△DOB是等腰三角形？如果存在，试求出所有符合条件的点D的坐标，如果不存在，请说明理由．

查看试题解析