山东省济南市历城区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-09 类型:期末考试
一、单选题
-
1. 下列常用APP的图标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列等式从左到右的变形,属于因式分解的是( )A、a(x-y)=ax-ay B、x2-1=(x+1)(x-1) C、(x+1)(x+3)=x2+4x+3 D、x2+2x+1=x(x+2)+13. 如图,在□ABCD中,∠BCD的平分线交BA的延长线于点E , AE=2,AD=5,则CD的长为( )
2. 下列等式从左到右的变形,属于因式分解的是( )A、a(x-y)=ax-ay B、x2-1=(x+1)(x-1) C、(x+1)(x+3)=x2+4x+3 D、x2+2x+1=x(x+2)+13. 如图,在□ABCD中,∠BCD的平分线交BA的延长线于点E , AE=2,AD=5,则CD的长为( ) A、4 B、3 C、2 D、1.54. 若关于x的一元二次方程 有两个不相等的实数根,则m的值可能是( )A、3 B、2 C、1 D、05. 下列各命题是真命题的是( )A、平行四边形既是轴对称图形及是中心对称图形 B、有一个角是直角的平行四边形是正方形 C、对角线相等的平行四边形是矩形 D、对角线互相垂直的四边形是菱形6. 新能源汽车节能、环保,越来越受消费者喜爱,我国新能源汽车近几年销量全球第一,销量逐年增加,2018年销量为125.6万辆,到2020年销量为130万辆,设年平均增长率为x , 可列方程为( )A、125.6(1-x)2-130 B、125.6(1+2x)=130 C、130(1-x)2=125.6 D、125.6(1+x)2=1307. 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,将△ABC绕点A顺时针旋转60°得到△AED , 连接BE , 则BE的长为( )
A、4 B、3 C、2 D、1.54. 若关于x的一元二次方程 有两个不相等的实数根,则m的值可能是( )A、3 B、2 C、1 D、05. 下列各命题是真命题的是( )A、平行四边形既是轴对称图形及是中心对称图形 B、有一个角是直角的平行四边形是正方形 C、对角线相等的平行四边形是矩形 D、对角线互相垂直的四边形是菱形6. 新能源汽车节能、环保,越来越受消费者喜爱,我国新能源汽车近几年销量全球第一,销量逐年增加,2018年销量为125.6万辆,到2020年销量为130万辆,设年平均增长率为x , 可列方程为( )A、125.6(1-x)2-130 B、125.6(1+2x)=130 C、130(1-x)2=125.6 D、125.6(1+x)2=1307. 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,将△ABC绕点A顺时针旋转60°得到△AED , 连接BE , 则BE的长为( ) A、5 B、4 C、3 D、28. 关于x的分式方程 + = 有增根x=-2,则k的值为( )A、-32 B、-23 C、23 D、329. 如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,2),则关于x的不等式x+m<kx﹣1的解集在数轴上表示正确的是( )
A、5 B、4 C、3 D、28. 关于x的分式方程 + = 有增根x=-2,则k的值为( )A、-32 B、-23 C、23 D、329. 如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,2),则关于x的不等式x+m<kx﹣1的解集在数轴上表示正确的是( ) A、
A、 B、
B、 C、
C、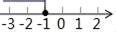 D、
D、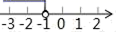 10. 如图,在△ABC中,AB=8,BC=12,点D、E分别是边AB、AC的中点,点F是线段DE上的一点,连接AF、BF , 若∠AFB=90°,则线段EF的长为( )
10. 如图,在△ABC中,AB=8,BC=12,点D、E分别是边AB、AC的中点,点F是线段DE上的一点,连接AF、BF , 若∠AFB=90°,则线段EF的长为( )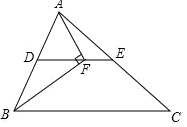 A、4 B、3 C、2 D、111. 关于x的方程 =1的解为正数,则a的取值范围是A、a>-2 B、a>-2且a≠-1 C、a>2 D、a>2且a≠312. 如图,正方形ABCD的边长为5,E为BC上一点,且BE=1,F为AB边上的一个动点,以EF为边向右侧作等边△EFG , 连接CG , 则CG的最小值为( )
A、4 B、3 C、2 D、111. 关于x的方程 =1的解为正数,则a的取值范围是A、a>-2 B、a>-2且a≠-1 C、a>2 D、a>2且a≠312. 如图,正方形ABCD的边长为5,E为BC上一点,且BE=1,F为AB边上的一个动点,以EF为边向右侧作等边△EFG , 连接CG , 则CG的最小值为( )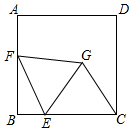 A、1 B、3 C、3 D、2.5
A、1 B、3 C、3 D、2.5二、填空题
-
13. 多项式x2+mx+5因式分解得(x+5)(x+n),则m= ,n= .14. 如图,一个直角三角形纸板的直角边 分别经过正八边形的两个顶点,则图中
 15. 如图,在Rt△ABC中,∠ACB=90°,∠A=52°,以点B为圆心、以BC的长为半径画弧,交AB于点D , 连接CD , 则∠ADC的度数为;
15. 如图,在Rt△ABC中,∠ACB=90°,∠A=52°,以点B为圆心、以BC的长为半径画弧,交AB于点D , 连接CD , 则∠ADC的度数为;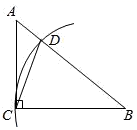 16. 如图,某小区规划在一个长为 、宽为 的矩形场地 上修建三条同样宽的小路,使其中两条与 平行,另一条与 平行,其余部分种草.若草坪部分的总面积为 ,则小路的宽度为m .
16. 如图,某小区规划在一个长为 、宽为 的矩形场地 上修建三条同样宽的小路,使其中两条与 平行,另一条与 平行,其余部分种草.若草坪部分的总面积为 ,则小路的宽度为m .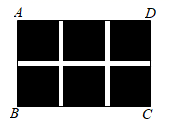 17. 如图,△ABC的面积为6cm2 , AP与∠B的平分线垂直,垂足是点P , 则△PBC的面积为;
17. 如图,△ABC的面积为6cm2 , AP与∠B的平分线垂直,垂足是点P , 则△PBC的面积为;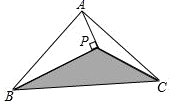 18. 正方形ABCD外取一点E , 连接AE、BE、DE , 过点A作AE的垂线交DE于点P , 若AE=AP=1,PB= .下列结论:①△APD≌△AEB;②EB⊥ED;③点B到直线AE的距离为 ;④S正方形ABCD=1+ .其中正确结论的序号是 .
18. 正方形ABCD外取一点E , 连接AE、BE、DE , 过点A作AE的垂线交DE于点P , 若AE=AP=1,PB= .下列结论:①△APD≌△AEB;②EB⊥ED;③点B到直线AE的距离为 ;④S正方形ABCD=1+ .其中正确结论的序号是 .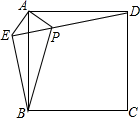
三、解答题
-
19.(1)、解不等式: - ≤1,并把解集在数轴上表示出来.(2)、解不等式(组): ,并求出它的所有的整数解的和.20. 分解因式(1)、4x2-9;(2)、3a-6a2+3a321. 计算(1)、化简: - ;(2)、化简求值:( -1)÷ ,其中x= .22. 解分式方程: + =-23. 用适当的方法解下列方程:x2-6x-3=024. 如图,在△ABC中,AC=BC , CD为∠ABC的角平分线,AE∥DC , AE=DC , 连接CE .
 (1)、求证:四边形ADCE为矩形(2)、连接DE , 若AB=10,CD=12,求DE的长.25. 如图,正方形网格中的每个小正方形边长都是一个单位长度,在平面直角坐标系中,△ABC为三个顶点分别是A(5,2),B(5,5),C(1,1).
(1)、求证:四边形ADCE为矩形(2)、连接DE , 若AB=10,CD=12,求DE的长.25. 如图,正方形网格中的每个小正方形边长都是一个单位长度,在平面直角坐标系中,△ABC为三个顶点分别是A(5,2),B(5,5),C(1,1). (1)、①画出△ABC向左平移5个单位得到的△A1B1C1 , 则点A的对应点A1的坐标为 ▲ ;
(1)、①画出△ABC向左平移5个单位得到的△A1B1C1 , 则点A的对应点A1的坐标为 ▲ ;②画出△A1B1C1绕点C顺时针旋转90°后得到的△A2B2C2 , 则点A1的对应点A2的坐标为 ▲ ;
(2)、请直接写出四边形A2B2B1C1的面积为;(3)、在平面上是否存在点D , 使得以A、B、C、D为顶点的四边形是平行四边形,若存在,请直接写出符合条件的所有点D的坐标,若不存在,请说明理由.26. 某电商响应市政府号召,在线销售甲、乙两种农产品,已知1件甲产品的售价是1件乙产品售价3倍,用300元购买甲产品的数量比用200元购买乙产品数量少20件.(1)、求甲、乙两种农产品每件的售价分别是多少元?(2)、如果某客户购买甲、乙两种农产品共40件,总费用不超过365元,请你帮忙计算,此客户最多购买甲产品多少件?27. 在正方形ABCD中,点P是CD边上点,点E在AP的延长线上,将线段AE绕点A顺时针旋转90°,到线段AF , 连接DE (1)、如图1,连接BF , 求证:BF=DE;(2)、如图2,若EF正好经过点B ,
(1)、如图1,连接BF , 求证:BF=DE;(2)、如图2,若EF正好经过点B ,①求证:DE⊥EF;
②探究BE、BF、BA三条线段的数量关系并证明你的结论;
(3)、如图3,当EF经过点C时,若CF=4,CE=2,请直接写出此时正方形边的长度).