山东省东营市垦利区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-09 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 =﹣5 B、4 ﹣3 =1 C、 × = D、 ÷ =92. 对于反比例函数 ,下列说法正确的是( )A、点(-2,1)在它的图象上 B、它的图象在第一、三象限 C、它的图象经过原点 D、当x>0时,y随x的增大而增大3. 已知 ,那么下列等式中,不一定正确的是( )A、2x=3y B、 C、 D、4. 使代数式 有意义的自变量x的取值范围是( )A、x≥3 B、x>3且x≠4 C、x≥3且x≠4 D、x>35. 如图,在△ABC中,CD,BE分别是△ABC的边AB,AC上的中线,则 ( )
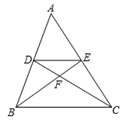 A、 B、 C、 D、6.
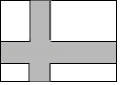
A、 B、 C、 D、6.如图,在宽为20米,长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,设道路的宽为x米,则下列方程正确的是( )
 A、32×20﹣20x﹣30x=540 B、32×20﹣20x﹣30x﹣x2=540 C、(32﹣x)(20﹣x)=540 D、32×20﹣20x﹣30x+2x2=5407. 如图,点A , B分别是反比例函数 (x<0)和 (x<0)图象上的点,且AB∥x轴,点C在x轴上,则△ABC的面积是( )
A、32×20﹣20x﹣30x=540 B、32×20﹣20x﹣30x﹣x2=540 C、(32﹣x)(20﹣x)=540 D、32×20﹣20x﹣30x+2x2=5407. 如图,点A , B分别是反比例函数 (x<0)和 (x<0)图象上的点,且AB∥x轴,点C在x轴上,则△ABC的面积是( ) A、4 B、5 C、6 D、88. 一个等腰三角形的两条边长分别是方程 的两根,则该等腰三角形的周长是( )A、12 B、9 C、13 D、12或99. 如图:在△ABC中,点D在BC边上,连接AD , 点G在线段AD上,GE BD , 且交AB于点E , GF AC , 且交CD于点F , 则下列结论一定正确的是( )
A、4 B、5 C、6 D、88. 一个等腰三角形的两条边长分别是方程 的两根,则该等腰三角形的周长是( )A、12 B、9 C、13 D、12或99. 如图:在△ABC中,点D在BC边上,连接AD , 点G在线段AD上,GE BD , 且交AB于点E , GF AC , 且交CD于点F , 则下列结论一定正确的是( )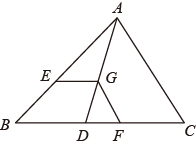 A、 B、 C、 D、10. 如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点O , CE与DA的延长线交于点E , 连接AC、BE、DO , 且DO与AC交于点F . 则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF∶AD=2∶5;④S四边形AFOE∶S△COD=2∶3.其中结论正确的有( )
A、 B、 C、 D、10. 如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点O , CE与DA的延长线交于点E , 连接AC、BE、DO , 且DO与AC交于点F . 则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF∶AD=2∶5;④S四边形AFOE∶S△COD=2∶3.其中结论正确的有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 化简 = .12. 已知x=1是一元二次方程 的一个根,则 的值为.13. 若 ,则 =.14. 如图,在 中,点E在边AD上,AE:AD=2:3,BE与AC交于点F.若AC=20,则AF的长为 .
 15. 规定: ,如: ,若 ,则 =.16. 如图,为了测量操场上一棵大树的高度,小英拿来一面镜子,平放在离树根部5m的地面上,然后她沿着树根和镜子所在的直线后退,当她后退1m时,正好在镜中看见树的顶端.小英估计自己的眼睛到地面的距离为1.6m,则大树的高度是m.
15. 规定: ,如: ,若 ,则 =.16. 如图,为了测量操场上一棵大树的高度,小英拿来一面镜子,平放在离树根部5m的地面上,然后她沿着树根和镜子所在的直线后退,当她后退1m时,正好在镜中看见树的顶端.小英估计自己的眼睛到地面的距离为1.6m,则大树的高度是m.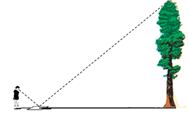 17. 如图,在直角坐标系中,以坐标原点O(0,0),A(0,4),B(-3,0)为顶点的Rt△AOB , 其两个锐角对应的外角角平分线相交于点P , 且点P恰好在反比例函数 的图象上,则k的值为 .
17. 如图,在直角坐标系中,以坐标原点O(0,0),A(0,4),B(-3,0)为顶点的Rt△AOB , 其两个锐角对应的外角角平分线相交于点P , 且点P恰好在反比例函数 的图象上,则k的值为 . 18. 如图,在平面直角坐标系中,矩形AOCB的两边OA , OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的 倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大 倍,得到矩形A2OC2B2……,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
18. 如图,在平面直角坐标系中,矩形AOCB的两边OA , OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的 倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大 倍,得到矩形A2OC2B2……,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
三、解答题
-
19.(1)、计算:(2)、解方程:x2-3x-10=020. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,3),B(4,1),C(1,1).
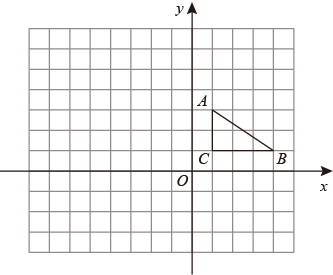
请解答下列问题:
⑴画出△ABC关于x轴成轴对称的△A1B1C1 , 并直接写出点B1的坐标;
⑵以原点O为位似中心,位似比为1∶2,在y轴的左侧,画出△A1B1C1放大后的图形△A2B2C2 , 并直接写出A2点的坐标.
21. 在国家精准扶贫的政策下,某乡镇企业职工人均收入大幅提高.2018年的人均收入为20000元,2020年的人均收入为39200元.(1)、若这两年的年平均增长率相同,求人均收入的年平均增长率;(2)、假设2021年该乡镇企业职工人均收入的增长率与前两年的年平均增长率相同,请你预测2021年职工的人均收入是多少元?22. 如图所示,△ABC中,BD⊥AC于点D , CE⊥AB于点E , BD与CE相交于点F . (1)、求证:△BEF∽△CDF;(2)、求证:DE·BF=EF·BC .23. 已知在平面直角坐标系中,点A(1,2)在反比例函数 的图象上,过点A的直线与该双曲线的另一支交于点B(-2,m).
(1)、求证:△BEF∽△CDF;(2)、求证:DE·BF=EF·BC .23. 已知在平面直角坐标系中,点A(1,2)在反比例函数 的图象上,过点A的直线与该双曲线的另一支交于点B(-2,m). (1)、求直线AB的函数解析式;(2)、若点C为x轴上一动点,求当S△ABC=6时,点C的坐标;(3)、观察图象,直接写出当x满足什么条件时,直线AB在双曲线的上方.24. 有一块直角三角形木板,∠B=90°,AB=1.5m,BC=2m,要把它加工成一个面积尽可能大的正方形桌面.甲、乙两位同学的加工方法分别如图1、图2所示.请你用学过的知识说明哪位同学的加工方法更好(加工损耗忽略不计).
(1)、求直线AB的函数解析式;(2)、若点C为x轴上一动点,求当S△ABC=6时,点C的坐标;(3)、观察图象,直接写出当x满足什么条件时,直线AB在双曲线的上方.24. 有一块直角三角形木板,∠B=90°,AB=1.5m,BC=2m,要把它加工成一个面积尽可能大的正方形桌面.甲、乙两位同学的加工方法分别如图1、图2所示.请你用学过的知识说明哪位同学的加工方法更好(加工损耗忽略不计).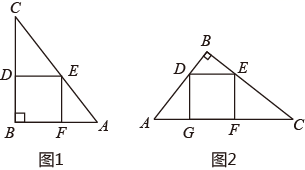 25. 先阅读理解下面的例题,再按要求解答下列问题:
25. 先阅读理解下面的例题,再按要求解答下列问题:例题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4
∵(y+2)2≥0,
∴(y+2)2+4≥4
∴y2+4y+8的最小值是4.
(1)、求代数式x2+2x+4的最小值;(2)、求代数式4-x2+2x的最大值;(3)、如图,某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园ABCD , 花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?