山东省德州市陵城区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-09 类型：期末考试

进入出卷网下载

一、单选题

1. 以下变形正确的是（）

A、 $\sqrt{2} + \sqrt{2} = \sqrt{4}$ B、 $3 \sqrt{2} = \sqrt{3 \times 2}$ C、 ${(\sqrt{2})}^{3} = 3 \sqrt{2}$ D、 $\frac{\sqrt{8}}{\sqrt{2}} = \sqrt{\frac{8}{2}}$

查看试题解析
2. 若代数式 $\frac{\sqrt{x}}{x - 2}$ 有意义，则x的取值范围是（）

A、x≥2 B、x≥0 C、x≥0且x≠2 D、x≠2

查看试题解析
3. 如图，在 $Δ A B C$ 中， $∠ A C B = 90 °$ ， $B C = 2$ ， $A C = 1$ ， $B C$ 在数轴上，以 $B$ 点为圆心， $A B$ 长为半径画弧，交数轴于点 $D$ ，则 $D$ 点表示的数是（）

A、 $3 - \sqrt{5}$ B、 $\sqrt{5}$ C、 $\sqrt{5} - 3$ D、 $3 - \sqrt{3}$

查看试题解析
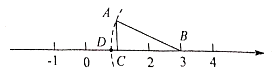4. 若关于x的方程（a﹣2）x²＋x＋1＝0是一元二次方程，则a的取值范围为（　　）

A、a＝2 B、a≠﹣2 C、a≠±2 D、a≠2

查看试题解析
5. 面试时，某人的基本知识、表达能力、工作态度的得分分别是90分、80分、85分，若依次按20%、40%、40%的比例确定成绩，则这个人的面试成绩是（）

A、82分 B、86分 C、85分 D、84分

查看试题解析
6. 已知一次函数 $y = k x + 1$ 的图象经过点A ，且函数值y随x的增大而减小，则点A的坐标可能是 $($ $)$

A、 $(2 ， 4)$ B、 $(- 1 ， 2)$ C、 $(- 1 ， - 4)$ D、 $(5 ， 1)$

查看试题解析
7. 如图，在平行四边形 $A B C D$ 中， $B F$ 平分 $∠ A B C$ ，交 $A D$ 于点 $F$ ， $C E$ 平分 $∠ B C D$ 交 $A D$ 于点 $E$ ， $A B = 6$ ， $B C = 10$ ，则 $E F$ 长为（）

A、1 B、2 C、3 D、4

查看试题解析
8. 如图，在△ABC中，点D，E分别是边AB，AC的中点，AF⊥BC，垂足为点F，∠ADE＝30°，DF＝3，则BF的长为（）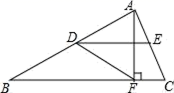

A、4 B、2 $\sqrt{3}$ C、3 $\sqrt{3}$ D、4 $\sqrt{3}$

查看试题解析
9. 如图1，在矩形MNPO中，动点R从点N出发，沿N→P→O→M方向运动至点M处停止．设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则矩形MNPO的周长是（）

A、11 B、15 C、16 D、24

查看试题解析
10. 如图，一次函数 $y = \frac{3}{4} x + 6$ 的图像与 $x$ 轴， $y$ 轴分别交于点 $A$ ， $B$ ，过点 $B$ 的直线 $l$ 平分 $Δ A B O$ 的面积，则直线 $l$ 相应的函数表达式为（）

A、 $y = \frac{3}{5} x + 6$ B、 $y = \frac{5}{3} x + 6$ C、 $y = \frac{2}{3} x + 6$ D、 $y = \frac{3}{2} x + 6$

查看试题解析
11. 如图，在平面直角坐标系中，四边形 $O A B C$ 为菱形， $O (0 ， 0)$ ， $A (4 ， 0)$ ， $∠ A O C = 60^{\circ}$ ，则对角线交点 $E$ 的坐标为（）

A、 $(2 ， \sqrt{3})$ B、 $(\sqrt{3} ， 2)$ C、 $(\sqrt{3} ， 3)$ D、 $(3 ， \sqrt{3})$

查看试题解析
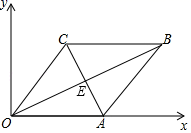12. 如图，在四边形 $A B C D$ 中， $A B = A D$ ， $B C = D C$ ， $A C$ ， $B D$ 交于点 $O$ .添加一个条件使这个四边形成为一种特殊的平行四边形，则以下说法错误的是（）

A、添加“ $A B // C D$ ”，则四边形 $A B C D$ 是菱形 B、添加“ $∠ B A D = 90 °$ ”，则四边形 $A B C D$ 是矩形 C、添加“ $O A = O C$ ”，则四边形 $A B C D$ 是菱形 D、添加“ $∠ A B C = ∠ B C D = 90 °$ ”，则四边形 $A B C D$ 是正方形

查看试题解析

二、填空题

13. 若 $y = 2 \sqrt{x - 3} + \sqrt{3 - x} + 6$ ，则xy的平方根为．

查看试题解析
14. 在Rt△ABC中，∠C＝90°，AB＝15， $\frac{B C}{A C} = \frac{3}{4}$ ，则BC＝.

查看试题解析
15. 若样本1，2，3，x的平均数为5，又知样本1，2，3，x，y的平均数为6，那么样本1，2，3，x，y的方差是．

查看试题解析
16. 设m ， n分别为一元二次方程x²＋2x－2 021＝0的两个实数根,则m²＋3m＋n＝.

查看试题解析
17. 如图，正方形AFCE中，D是边CE上一点，B是CF延长线上一点，且AB=AD，若四边形ABCD的面积是24cm² ．则AC长是cm．

查看试题解析
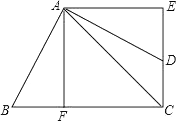18. 疫情之下，中华儿女共抗时艰.重庆和湖北同饮长江水，为更好地驰援武汉，打赢防疫攻坚战，我市某公益组织收集社会捐献物资.甲、乙两人先后从 $A$ 地沿相同路线出发徒步前往 $B$ 地进行物资捐献，甲出发1分钟后乙再出发，一段时间后乙追上甲，这时甲发现有东西落在 $A$ 地，于是原路原速返回 $A$ 地去取（甲取东西的时间忽略不计），而乙继续前行，甲乙两人到达B地后原地帮忙.已知在整个过程中，甲乙均保持各自的速度匀速行走，甲、乙两人相距的路程 $y$ （米）与甲出发的时间 $x$ （分钟）之间的函数关系如图所示，则当乙到达 $B$ 地时，甲距 $A$ 地的路程是米.

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{18}$ ﹣4 $\sqrt{\frac{1}{2}}$ + $\sqrt{24}$ ÷ $\sqrt{3}$ ；

(2)、（1﹣ $\sqrt{3}$ ）（1+ $\sqrt{3}$ ）+（1+ $\sqrt{3}$ ）² ．

查看试题解析
20. 已知关于x的方程 $x^{2} + a x + a - 2$ =0.

(1)、求证：不论a取何实数，该方程都有两个不相等的实数根。

(2)、当a=1时，求该方程的根。

查看试题解析

21. 某学校八年级开展英语拼写大赛，一班和二班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩如图所示：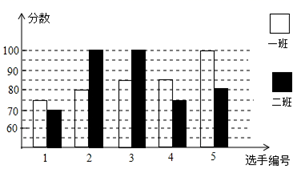

(1)、根据图示填写下表

班级	中位数（分）	众数（分）	平均数（分）
一班	85
二班		100	85

(2)、结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩比较好？

(3)、已知一班的复赛成绩的方差是70，请求出二班复试成绩的方差，并说明哪个班成绩比较稳定？

查看试题解析

22. 笔直的河流一侧有一旅游地C，河边有两个漂流点A、B，其中AB=AC，由于某种原因，由C到A的路现在已经不通，为方便游客，决定在河边新建一个漂流点H(A，H，B在一条直线上)，并新修一条路CH，测得BC=5千米，CH=4千米，BH=3千米，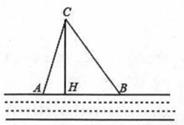

(1)、问CH是否为从旅游地C到河的最近的路线？请通过计算加以说明；

(2)、求原来路线AC的长。

查看试题解析
23. 过矩形ABCD的对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE，CF．

(1)、求证：四边形AECF是菱形；

(2)、若AB＝6，AC＝10，EC＝ $\frac{25}{4}$ ，求EF的长．

查看试题解析
24. 某水果店11月份购进甲、乙两种水果共花费1700元，其中甲种水果8元/千克，乙种水果18元/千克.12月份，这两种水果的进价上调为：甲种水果10元/千克，乙种水果20元/千克．

(1)、若该店12月份购进这两种水果的数量与11月份都相同，将多支付货款300元，求该店11月份购进甲、乙两种水果分别是多少千克？

(2)、若12月份将这两种水果进货总量减少到120千克，设购进甲种水果a千克，需要支付的货款为w元，求w与a的函数关系式；

(3)、在（2）的条件下，若甲种水果不超过90千克，则12月份该店需要支付这两种水果的货款最少应是多少元？

查看试题解析
25. 在四边形 ABCD 中，对角线 AC、BD 相交于点 O，过点 O 的两条直线分别交边 AB、CD、AD、BC 于点 E、F、G、H．

(1)、如图①，若四边形 ABCD 是正方形，且 AG＝BE＝CH＝DF，则 S_四边形_AEOG＝S_正方形_ABCD；

(2)、如图②，若四边形 ABCD 是矩形，且 S_四边形_AEOG＝ $\frac{1}{4}$ S_矩形_ABCD ，设 AB＝a， AD＝b，BE＝m，求 AG 的长（用含 a、b、m 的代数式表示）；

(3)、如图③，若四边形 ABCD 是平行四边形，且 AB＝3，AD＝5，BE＝1，试确定 F、G、H 的位置，使直线 EF、GH 把四边形 ABCD 的面积四等分．

查看试题解析