山东省滨州市滨城区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子是最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{\frac{2}{3}}$ C、 $\sqrt{0.5}$ D、 $\sqrt{30}$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{{(- 6)}^{2}} = - 6$ B、 ${(- 2 \sqrt{7})}^{2} = 14$ C、 $\sqrt{4 \frac{1}{9}} = 2 \frac{1}{3}$ D、 $\sqrt{12} \div \sqrt{3} = 2$

查看试题解析
3. 函数 $y = \frac{1}{\sqrt{2 - x}}$ 中，自变量 $x$ 的取值范围是（）

A、 $x \neq 2$ B、 $x > 2$ C、 $x < 2$ D、 $x \leq 2$

查看试题解析
4. 下列二次根式，化简后能与 $- \sqrt{5}$ 合并的是（）

A、 $\sqrt{25}$ B、 $\sqrt{20}$ C、 $\sqrt{15}$ D、 $\sqrt{10}$

查看试题解析
5. 下列命题的逆命题成立的是（）

A、若 $a = b$ ，则 $\sqrt{a^{2}} = \sqrt{b^{2}}$ B、对顶角相等 C、对角线互相平分的四边形是平行四边形 D、矩形的对角线相等

查看试题解析
6. 关于一次函数 $y = - 3 x + 2$ ，下列说法正确的是（）

A、图象经过点 $(2 ， 0)$ B、图象经过第三象限 C、函数 $y$ 随自变量 $x$ 的增大而增大 D、当 $x \geq \frac{2}{3}$ 时， $y \leq 0$

查看试题解析
7. 体育课上甲、乙两同学比赛跑步，其路程 $S$ （单位： $m$ ）与时间 $t$ （单位： $s$ ）之间的图象如图所示，下列说法错误的是（）

A、甲、乙进行的是 $100 m$ 赛跑 B、甲的平均速度大于乙的平均速度 C、前 $3 s$ ，甲的速度大于乙的速度 D、甲、乙同时到达终点

查看试题解析
8. 某校为落实作业管理、睡眠管理、手机管理、读物管理、体质管理工作有关要求，随机抽查了部分学生每天的睡眠时间，制定如下统计表．

睡眠时间/ $h$

6

7

8

9

人数

10

20

15

5

则所抽查学生每天睡眠时间的平均数为（）

A、 $7 h$ B、 $7.3 h$ C、 $7.5 h$ D、 $8 h$

查看试题解析
9. 某村欲购进一批杏树，考察中随机从甲、乙、丙、丁四个品种中各选了10棵，每棵产量（单位： $kg$ ）的平均数 $\bar{x}$ 及方差 $s^{2}$ 如表所示：

统计量

甲

乙

丙

丁

$\bar{x}$

40

40

38

38

$s^{2}$

1.5

2.3

1.8

2.3

该村准备从这四个品种中选出一种产量既高又稳定的杏树，则应选的品种是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
10. 满足下列条件时， $△ A B C$ 不是直角三角形的为（）

A、 $A B = 5$ ， $B C = 13$ ， $A C = 12$ B、 $A B ： B C ： A C = 3 ： 4 ： 5$ C、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$ D、中线 $C D = \frac{1}{2} A B$

查看试题解析
11. 小明在做“练习使用弹簧测力计”的实验时，用 $x$ （单位： $N$ ）表示弹簧受到的拉力，用 $y$ （单位： $cm$ ）表示挂上重物后弹簧的总长（在弹性范围内， $y$ 是 $x$ 一次函数）．记录实验数据如下：

$x$

1

2.5

3

……

$y$

5

8

9

……

小明得出下列结论：①弹性范围内， $y$ 与 $x$ 的关系式是 $y = 2 x + 3$ ；②不挂重物时弹簧的长度为 $3 cm$ ；③若弹簧总长不能超过 $13 cm$ ，则弹簧所受到的拉力不能超过 $5 N$ ；④弹性范围内，弹簧伸长的长度与弹簧所受拉力成正比．其中正确结论的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
12. 如图，在平面直角坐标系中，菱形ABCD的顶点A在 $y$ 轴上，顶点B ， C的坐标分别为(−6，0)，(4，0)，则点 $D$ 的坐标是（）

A、 $(6 ， 8)$ B、 $(10 ， 8)$ C、 $(10 ， 6)$ D、 $(4 ， 6)$

查看试题解析

二、填空题

13. 计算： $\sqrt{8} - {(\frac{\sqrt{2}}{2})}^{- 1} - (\sqrt{2} + 1) {(\sqrt{2} - 1)}^{2} =$ ．

查看试题解析
14. 如图，在四边形ABCD中，AD//BC，在不添加任何辅助线的情况下，请你添加一个条件，使四边形ABCD是平行四边形（填一个即可）．

查看试题解析
15. 如图，在矩形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ， $∠ A O B = 60 °$ ， $A C = 6$ ，则 $B C$ 的长是．

查看试题解析
16. 如图，在 $△ A B C$ 中，点 $D$ ， $E$ 分别是边 $A B$ ， $A C$ 的中点，点 $F$ 是线段 $D E$ 上的一点，连接 $A F$ ， $B F$ ， $∠ A F B = 90 °$ ．已知 $A B = 6$ ， $B C = 10$ ，则 $E F$ 的长是．

查看试题解析
17. 若一组数据4，x ， 5，7，9的平均数为6，则这组数据的方差为．

查看试题解析
18. 已知正比例函数的图象过点(2，4)．把该函数图象平移，使它过点(1，−1)，则平移后所得函数的解析式是．

查看试题解析
19. 某生态体验园推出了甲、乙两种消费卡．甲、乙两卡所需费用 $y_{甲}$ ， $y_{乙}$ （单位：元）与入园次数 $x$ （单位：次）的函数关系如图所示．当x满足时， $y_{甲} > y_{乙}$ ．

查看试题解析
20. 如图，正方形ABCD中，AB=6，点E在边CD上，且DE=2．将△ADE沿AE对折至△AFE ，延长EF交BC于点G ，连接AG ， CF ．下列结论：①△ABG≌△AFG；②∠GAE=45°；③BG=GC；④AG//CF；⑤△CFE是等腰三角形，其中正确的结论有（填写所有正确结论的序号）．

查看试题解析

三、解答题

21. 书籍是人类进行的阶梯．为了解学生的课外阅读情况，某校随机抽查了部分学生本学期阅读课外书的册数，并绘制出如下统计图．

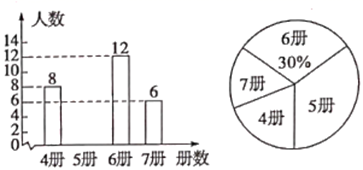(1)、共抽查了多少名学生？

(2)、请补全条形统计图，并写出被抽查学生本学期阅读课外书册数的众数、中位数；

(3)、根据抽查结果，请估计该校1200名学生中本学期课外阅读5册书的学生人数．

查看试题解析
22. 如图，在▱ABCD中，对角线AC与BD相交于点O ，过点O的直线EF与BA ， DC的延长线分别交于点E ， F ，连接BF ， DE ．

(1)、求证：AE=CF；

(2)、请添加一个条件，使四边形BFDE是菱形，并说明理由．

查看试题解析
23. 5G时代的到来，给人类生活带来巨大变化．现有A ， B两种型号的5G手机，已知销售1部A型手机和1部B型手机共获利700元，销售6部A型手机和4部B型手机共获利3400元．

(1)、请问1部A型手机和1部B型手机的利润分别为多少元？

(2)、某营业厅计划购进A ， B两种型号手机共30部，其中B型手机的数量不多于A型手机数量的2倍．两种型号手机各购进多少部，全部销售后获利最大？最大利润是多少？

查看试题解析
24. 勾股定理是人类重大科学发现之一．我国古代数学书《周髀算经》记载，约公元前11世纪，我国古代劳动人民就知道“若勾三，股四，则弦五”，比西方早500多年．请你运用学到的知识、方法和思想探究以下问题．

(1)、（探究一）我国汉代数学家赵爽创制了“赵爽弦图”，通过图形切割、拼接，巧妙地利用面积关系证明了勾股定理．古往今来，人们对勾股定理的证明一直保持着极大的热情．意大利著名画家达·芬奇用两张一样的纸片，拼出不一样的空洞，利用空洞面积相等也成功地证明了勾股定理（如图）．
请你写出这一证明过程（图中所有的四边形都是正方形，三角形都是直角三角形）．

(2)、（探究二）在学习勾股定理的过程中，我们获得了以下数学活动经验：分别以直角三角形的三边为边向外侧作正方形（如图2），它们的面积 $S_{1}$ ， $S_{2}$ ， $S_{3}$ 之间满足的等量关系是：．

(3)、迁移应用：如图3，图中所有的四边形都是正方形，三角形都是直角三角形．若正方形 $A$ ， $B$ ， $C$ ， $D$ 的边长分别是 $3$ ， $5$ ， $3$ ， $2$ ，则正方形 $E$ 的面积是．

(4)、（探究三）如图4，分别以直角三角形的三边为直径向外侧作半圆，则它们的面积 $S_{1}$ ， $S_{2}$ ， $S_{3}$ 之间满足的等量关系是．

(5)、迁移应用：如图5，直角三角形的两条直角边长分别为 $a$ ， $b$ ，斜边长为 $c$ ，分别以三边为直径作半圆．若 $a = 5$ ， $c = 13$ ，则图中阴影部分的面积等于．

(6)、（探究四）《九章算术》卷九“勾股”中记载：今有立木，系索其末，委地三尺．引索却行，去本八尺而索尺．问索长几何．译文：今有一竖立着的木柱，在木桩的上端系有绳索，绳索从木柱上端顺木柱下垂后，堆在地面的部分尚有 $3$ 尺．牵着绳索（绳索与地面接触）退行，在距木柱根部 $8$ 尺处时绳索用尽．问绳索长多少？

查看试题解析
25. 李明酷爱数学，勤于思考，善于反思．在学习八年级下册数学知识之后，他发现“二次根式、勾股定理、一次函数、平行四边形”都和“将军饮马”问题有关联，并且为解决“饮马位置”“最短路径长”等问题，提供了具体的数学方法．于是他撰写了一篇数学作文．请你认真阅读思考，帮助李明完成相关问题．
“将军饮马”问题的探究与拓展

八年级三班李明

“白日登山望烽火，黄昏饮马傍交河”（唐·李颀《古从军行》），这句诗让我想到了有趣的“将军饮马”问题：将军从 $A$ 地出发到河边 $l$ 饮马，然后再到 $B$ 地军营视察，怎样走路径最短？

（数学模型）如图1， $A$ ， $B$ 是直线 $l$ 同旁的两个定点．在直线 $l$ 上确定一点 $P$ ，使 $P A + P B$ 的值最小．

（问题解决）作点 $A$ 关于直线 $l$ 的对称点 $A^{'}$ ，连接 $A^{'} B$ 交 $l$ 于点 $P$ ，则点 $P$ 即为所求．此时， $P A + P B$ 的值最小，且 $P A + P B = A^{'} P + P B = A^{'} B$ ．

(1)、（模型应用）
问题1．如图2，经测量得 $A$ ， $B$ 两点到河边 $l$ 的距离分别为 $A C = 300$ 米， $B D = 900$ 米，且 $C D = 900$ 米．请计算出“将军饮马”问题中的最短路径长．

(2)、问题2．如图3，在正方形 $A B C D$ 中， $A B = 9$ ，点 $E$ 在 $C D$ 边上，且 $D E = 2 C E$ ，点 $P$ 是对角线 $A C$ 上的一个动点，则 $P E + P D$ 的最小值是．

(3)、问题3．如图4，在平面直角坐标系中，点 $A (- 2 ， 4)$ ，点 $B (4 ， 2)$ ．

请在 $x$ 轴上确定一点 $P$ ，使 $P A + P B$ 的值最小，并求出 $P$ 的坐标；

(4)、请直接写出 $P A + P B$ 的最小值．

(5)、（模型迁移）
问题4．如图5，菱形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ， $A C = 12$ ， $B D = 16$ ．点 $P$ 和点 $E$ 分别为 $B D$ ， $C D$ 上的动点，求 $P E + P C$ 的最小值．

查看试题解析

睡眠时间/ $h$	6	7	8	9
人数	10	20	15	5

统计量	甲	乙	丙	丁
$\bar{x}$	40	40	38	38
$s^{2}$	1.5	2.3	1.8	2.3

$x$	1	2.5	3	……
$y$	5	8	9	……