江西省吉安市吉州区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-09 类型：期末考试

进入出卷网下载

一、单选题

1. 保护环境，人人有责．下列四个图形是生活中常见的垃圾回收标志，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ，下列条件中，一定能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $O A = O C$ ， $O B = O D$ B、 $A D // B C$ C、 $A B = C D$ ， $A D // B C$ D、 $A C ⊥ B D$

查看试题解析
3. 如图所示的六边形花环是用六个全等的直角三角形拼成的，则∠ABC等于（）

A、30° B、35° C、45° D、60°

查看试题解析
4. 下列说法错误的是（）

A、若a＋3＞b＋3，则a＞b B、若 $\frac{a}{1 + c^{2}} > \frac{b}{1 + c^{2}}$ ，则a＞b C、若a＞b，则ac＞bc D、若a＞b，则a＋3＞b＋2

查看试题解析
5. 随着市场对新冠疫苗需求越来越大，为满足市场需求，某大型疫苗生产企业更新技术后，加快了生产速度，现在平均每天比更新技术前多生产10万份疫苗，现在生产500万份疫苗所需的时间与更新技术前生产400万份疫苗所需时间相同，设更新技术前每天生产x万份，依据题意得（）

A、 $\frac{400}{x - 10} = \frac{500}{x}$ B、 $\frac{400}{x} = \frac{500}{x + 10}$ C、 $\frac{400}{x} = \frac{500}{x - 10}$ D、 $\frac{400}{x + 10} = \frac{500}{x}$

查看试题解析
6. 如图，将 $▱ A B C D$ 沿对角线 $A C$ 进行折叠，折叠后点 $D$ 落在点 $F$ 处， $A F$ 交 $B C$ 于点 $E$ ，有下列结论：① $△ A B F ≌ △ C F B$ ；② $A E = C E$ ；③ $B F // A C$ ；④ $B E = C E$ ，其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

7. 将 $3 x^{2} y - 27 y$ 因式分解为.

查看试题解析
8. 若点 $P (m ， - 2)$ 与点 $Q (3 ， n)$ 关于原点对称，则 $m^{n} =$ ．

查看试题解析
9. 一次函数y=ax+b与正比例函数y=kx在同一平面直角坐标系的图象如图所示，则关于x的不等式ax+b≥kx的解集为．

查看试题解析
10. 已知关于x的方程 $\frac{2 x + m}{x - 2}$ =3的解是正数，则m的取值范围是．

查看试题解析
11. 如图，将直角梯形 $A B C D$ 沿 $A B$ 方向向下平移 $2$ 个单位得到直角梯形 $E F G H$ ，已知 $B C = 6$ ， $∠ A = 90 °$ ， $∠ C = 45 °$ ，则阴影部分的面积为．

查看试题解析
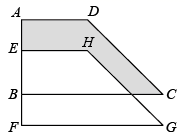12. 已知在直角三角形中，若一条直角边是斜边的一半，那么这条直角边所对的锐角为 $30 °$ ．若在等腰三角形 $A B C$ 中， $A D ⊥ B C$ 于点 $D$ ，且 $A D = \frac{1}{2} B C$ ，则 $△ A B C$ 顶角的度数为．

查看试题解析

三、解答题

13.

(1)、分解因式： $a^{3} + 10 a^{2} + 25 a$ ；

(2)、解方程： $\frac{2}{x + 2} + 1 = \frac{x}{x - 1}$ ．

查看试题解析
14. 解不等式组 ${\begin{array}{l} 2 x \leq 8 \\ \frac{3 x + 2}{2} > x \end{array}$ ，井把它的解集在数轴上表示出来．

查看试题解析
15. 如图，在四边形 $A B C D$ 中， $A B$ ∥ $C D$ ， $A B$ =2 $C D$ ， $E$ 为 $A B$ 的中点，请仅用无刻度的直尺分别按下列要求画图（保留作图痕迹）

(1)、在图1中，画出△ABD的BD边上的中线；

(2)、在图2中，若BA=BD，画出△ABD的AD边上的高.

查看试题解析
16. 先化简： $\frac{x^{2}}{x - 1} \div (1 + \frac{1}{x^{2} - 1})$ ，再从绝对值小于 $2$ 的数中选择一个合适的 $x$ 代入求值．

查看试题解析
17. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D ⊥ B C$ 于点D ．

(1)、若 $∠ B = 39 °$ ，求 $∠ C A D$ 的度数；

(2)、若点E在边 $A C$ 上， $E F // A B$ 交 $A D$ 的延长线于点F ．求证： $A E = F E$ ．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = 12 cm$ ， $A C = 8 cm$ ， $A D$ 、 $A E$ 分别是其角平分线和中线，过点 $C$ 作 $C G ⊥ A D$ 于点 $F$ ，交 $A B$ 于点 $G$ ，连接 $E F$ ．

(1)、说明： $A C = A G$ ；

(2)、求线段 $E F$ 的长．

查看试题解析
19. 请看下面的问题：把 $x^{4} + 4$ 分解因式．分析：这个二项式既无公因式可提，也不能直接利用公式，怎么办呢？19世纪的法国数学家苏菲·热门抓住了该式只有两项，而且属于平方和 ${(x^{2})}^{2} + 2^{2}$ 的形式，要使用公式就必须添一项 $4 x^{2}$ ，随即减去此项 $4 x^{2}$ ，即可得：
$x^{4} + 4$

$= x^{4} + 4 x^{2} + 4 - 4 x^{2}$

$= {(x^{2} + 2)}^{2} - {(2 x)}^{2}$

$= (x^{2} + 2 x + 2) (x^{2} - 2 x + 2)$

人们为了纪念苏菲·热门给出这一解法，就把它叫做“热门定理”，请你依照苏菲·热门的做法，将下列各式因式分解．

(1)、 $4 x^{4} + y^{4}$ ；

(2)、 $x^{2} - 2 a x - b^{2} - 2 a b$ ．

查看试题解析
20. 为落实帮扶措施，确保精准扶贫工作有效开展，加快贫困群众早日脱贫步伐，经过前期对贫困户情况摸排了解，结合贫困户实际养殖意愿，某扶贫工作队开展精准扶贫“送鸡苗”活动，该工作队为帮扶对象购买了一批土鸡苗和乌鸡苗，已知一只土鸡苗比一只乌鸡苗贵2元，购买土鸡苗的费用和购买乌鸡苗的费用分别是3500元和2500元

(1)、若两种鸡苗购买的数量相同，求鸟鸡苗的单价；

(2)、若两种鸡苗共购买1100只，且购买两种鸡苗的总费用不超过6000元，其中土鸡苗至少购买200只，根据（1）中两种鸡苗的单价，该工作队最少花费多少元？

查看试题解析
21. 如图，在 $▱ A B C D$ 中， $A B = 12 cm$ ， $B C = 6 cm$ ， $∠ A = 60 °$ ，点 $P$ 沿 $A B$ 边从点 $A$ 开始以 $2 cm$ /秒的速度向点 $B$ 移动，同时点 $Q$ 沿 $D A$ 边从点 $D$ 开始以 $1 cm$ /秒的速度向点 $A$ 移动，用 $t$ 表示移动的时间（ $0 \leq t \leq 6$ ）．

(1)、当 $t$ 为何值时， $△ P A Q$ 是等边三角形；

(2)、当 $t$ 为何值时， $△ P A Q$ 是直角三角形．

查看试题解析
22. 在 $△ A B C$ 中， $A B = A C$ ， $∠ A = 60 °$ ，点 $D$ 是线段 $B C$ 的中点， $∠ E D F = 120 °$ ， $D E$ 与线段 $A B$ 相交于点 $E$ ． $D F$ 与线段 $A C$ （或 $A C$ 的延长线）相交于点 $F$ ．

(1)、如图1，若 $D F ⊥ A C$ ，垂足为 $F$ ， $A B = 4$ ，求 $B E$ 的长；

(2)、如图2，将（1）中的 $∠ E D F$ 绕点 $D$ 顺时针旋转一定的角度， $D F$ 仍与线段 $A C$ 相交于点 $F$ ．求证： $B E + C F = \frac{1}{2} A B$ ；

(3)、如图3，将（2）中的 $∠ E D F$ 继续绕点 $D$ 顺时针旋转一定的角度，使 $D F$ 与线段 $A C$ 的延长线相交于点 $F$ ，作 $D N ⊥ A C$ 于点 $N$ ，若 $D N = F N$ ，求证： $B E + C F = \sqrt{3} (B E - C F)$ ．

查看试题解析
23. 在 $▱ A B C D$ 中， $∠ A D C$ 的平分线交 $B C$ 于点 $E$ ．交 $A B$ 的延长线于点 $F$ ，连接 $A C$

(1)、如图1，若 $∠ A D C = 90 °$ ， $G$ 是 $E F$ 的中点，连接 $A G$ 、 $C G$ ．
①求证： $B E = B F$ ．

②请判断 $△ A G C$ 的形状，并说明理由；

(2)、如图2，若 $∠ A D C = 60 °$ ，将线段 $F B$ 绕点 $F$ 顺时针旋转 $60 °$ 至 $F G$ ，连接 $A G$ 、 $C G$ ，请判断 $△ A G C$ 的形状，并说明理由．

(3)、如图3， $∠ A D C = 90 °$ ，作 $∠ B E D$ 的角平分线 $E H$ 交 $A B$ 于点 $H$ ，已知 $A B = 9$ ， $B H = 2 A H$ ，求 $B C$ 的长．

查看试题解析