江西省赣州市章贡区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-09 类型:期末考试
一、单选题
-
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 某校将举办一场“中国汉字听写大赛”,要求每班推选一名同学参加比赛,为此,初二(1)班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是96分,甲的成绩的方差是0.3,乙的成绩的方差是0.4,根据以上数据,下列说法正确的是( )A、甲的成绩比乙的成绩稳定 B、乙的成绩比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定甲、乙的成绩谁更稳定3. 若把一次函数y=2x﹣3的图象向上平移3个单位长度,得到图象对应的函数解析式为( )A、y=2x B、y=2x﹣6 C、y=4x﹣3 D、y=﹣x﹣34. 如图,已知四边形ABCD是平行四边形,下列结论中错误的是()
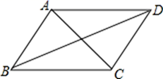 A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形5. 如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是( )
A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形5. 如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是( )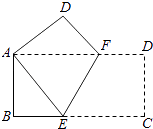 A、 B、 C、 D、6. 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )
A、 B、 C、 D、6. 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( ) A、4 B、8 C、16 D、8
A、4 B、8 C、16 D、8二、填空题
-
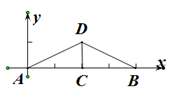
7. 使 有意义的x的取值范围是 .8. 菱形的两条对角线长分别为3和4,则菱形的面积是 .9. 若y= ,则x+y= .10. 如图,长为8 cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3 cm到点D,则橡皮筋被拉长了 cm.
 11. 直线 与 的交点的横坐标为 .则关于 的不等式 的解集为 .
11. 直线 与 的交点的横坐标为 .则关于 的不等式 的解集为 . 12. 如图所示,已知△ABC中, , , ,点P是△ABC边上的一个动点,点P从点A开始沿A→B→C→A方向运动,且速度为每秒4cm,设出发的时间为 ,当点P在边CA上运动时,若△ABP为等腰三角形,则运动时间 .
12. 如图所示,已知△ABC中, , , ,点P是△ABC边上的一个动点,点P从点A开始沿A→B→C→A方向运动,且速度为每秒4cm,设出发的时间为 ,当点P在边CA上运动时,若△ABP为等腰三角形,则运动时间 .
三、解答题
-
13. 计算:(1)、 ;(2)、直角三角形 中, 是斜边 的中,两直角边 , ,求 的长.
 14. 若 ,请判断以 、 、 为三边的 的形状并说明理由.15. 先化简,再求值:其中 ; ,16. 在图1,图2中,点E是矩形ABCD边AD的中点,请用无刻度的直尺按下列要求画图(保留画图痕迹,不写画法)
14. 若 ,请判断以 、 、 为三边的 的形状并说明理由.15. 先化简,再求值:其中 ; ,16. 在图1,图2中,点E是矩形ABCD边AD的中点,请用无刻度的直尺按下列要求画图(保留画图痕迹,不写画法) (1)、在图1中,以AE为一边在矩形外部画△AEP,使△AEP的面积等于矩形ABCD的面积的 .(2)、在图2中,以AE为对角线画一个平行四边形.17. 四边形 中, , , , ,垂足分别为 、 .求证:四边形 是平行四边形
(1)、在图1中,以AE为一边在矩形外部画△AEP,使△AEP的面积等于矩形ABCD的面积的 .(2)、在图2中,以AE为对角线画一个平行四边形.17. 四边形 中, , , , ,垂足分别为 、 .求证:四边形 是平行四边形 18. 学习“一次函数”时,我们从“数”和“形”两方面研究一次函数的性质,并积累了一些经验和方法,尝试用你积累的经验和方法解决下面问题.
18. 学习“一次函数”时,我们从“数”和“形”两方面研究一次函数的性质,并积累了一些经验和方法,尝试用你积累的经验和方法解决下面问题. (1)、在平面直角坐标系中,画出函数y=|x|的图象:
(1)、在平面直角坐标系中,画出函数y=|x|的图象:①列表:完成表格
x
…
﹣3
﹣2
﹣1
0
1
2
3
…
y
…
②画出y=|x|的图象;
(2)、结合所画函数图象,写出y=|x|两条不同类型的性质;(3)、写出函数y=|x|与y=|x﹣2|图象的平移关系.19. 某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况,并统计绘制成了如图两幅不完整的条形统计图和扇形统计图,请根据所提供的信息,解答下列问题: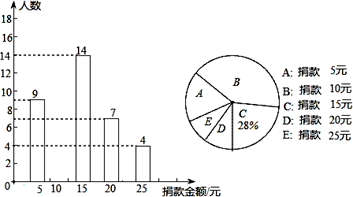 (1)、本次共抽查学生 ▲ 人,并将条形图补充完整;(2)、捐款金额的众数是 , 中位数是;(3)、在八年级850名学生中,捐款20元及以上(含20元)的学生估计有多少人?20. 如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形,AC、DE相交于点O.
(1)、本次共抽查学生 ▲ 人,并将条形图补充完整;(2)、捐款金额的众数是 , 中位数是;(3)、在八年级850名学生中,捐款20元及以上(含20元)的学生估计有多少人?20. 如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形,AC、DE相交于点O. (1)、求证:四边形ADCE是矩形.(2)、若∠AOE=60°,AE=4,求矩形ADCE对角线的长.21. 如图, 为线段 上一动点,分别过点 作 , ,连接 .已知 ,设 .
(1)、求证:四边形ADCE是矩形.(2)、若∠AOE=60°,AE=4,求矩形ADCE对角线的长.21. 如图, 为线段 上一动点,分别过点 作 , ,连接 .已知 ,设 . (1)、用含 的代数式表示 的值;(2)、探究:当点 满足什么条件时, 的值最小?最小值是多少?(3)、根据(2)中的结论,请构造图形求代数式 的最小值.22. 如图,直线 与 轴交于点 ,与 轴交于点 ;直线 与 轴交于点 ,与直线 交于点 ,且点 的纵坐标为4.
(1)、用含 的代数式表示 的值;(2)、探究:当点 满足什么条件时, 的值最小?最小值是多少?(3)、根据(2)中的结论,请构造图形求代数式 的最小值.22. 如图,直线 与 轴交于点 ,与 轴交于点 ;直线 与 轴交于点 ,与直线 交于点 ,且点 的纵坐标为4. (1)、不等式 的解集是;(2)、求直线 的解析式及 的面积;(3)、点 在坐标平面内,若以 、 、 、 为顶点的四边形是平行四边形,求符合条件的所有点 的坐标.23. 如图,我们把对角线互相垂直的四边形叫做垂美四边形.
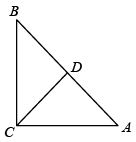
(1)、不等式 的解集是;(2)、求直线 的解析式及 的面积;(3)、点 在坐标平面内,若以 、 、 、 为顶点的四边形是平行四边形,求符合条件的所有点 的坐标.23. 如图,我们把对角线互相垂直的四边形叫做垂美四边形. (1)、概念理解:如图,在四边形 中, , ,问四边形 是垂美四边形吗?请说明理由.
(1)、概念理解:如图,在四边形 中, , ,问四边形 是垂美四边形吗?请说明理由. (2)、性质探究:试探究垂美四边形 两组对边 , 与 , 之间的数量关系,写出证明过程(先画出图形)(3)、问题解决:如图,分别以 的直角边 和斜边 为边向外作正方形 和正方形 ,连接 , , 已知 , ,求 的长.
(2)、性质探究:试探究垂美四边形 两组对边 , 与 , 之间的数量关系,写出证明过程(先画出图形)(3)、问题解决:如图,分别以 的直角边 和斜边 为边向外作正方形 和正方形 ,连接 , , 已知 , ,求 的长.