江西省赣州市经开区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-08-09 类型:期末考试
一、单选题
-
1. 的值是( )A、4 B、2 C、±4 D、±22. 以下列各组数为边长能构成直角三角形的是( )A、7,12,13 B、3,4,5 C、8,10,16 D、5,12,143.
如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,若菱形ABCD的周长为20,则OH的长为( )
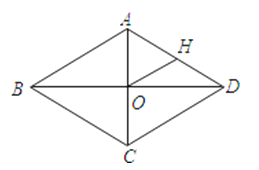 A、2 B、2.5 C、3 D、3.54. 在2021年的生物操作模拟考试中,甲、乙、丙、丁四个班级的平均分相同,方差分别为: , , , ,则四个班体考成绩最稳定的是( )A、甲班 B、乙班 C、丙班 D、丁班5. 如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )
A、2 B、2.5 C、3 D、3.54. 在2021年的生物操作模拟考试中,甲、乙、丙、丁四个班级的平均分相同,方差分别为: , , , ,则四个班体考成绩最稳定的是( )A、甲班 B、乙班 C、丙班 D、丁班5. 如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )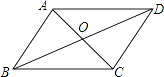 A、OA=OC,AD∥BC B、∠ABC=∠ADC,AD∥BC C、AB=DC,AD=BC D、∠ABD=∠ADB,∠BAO=∠DCO6. 如图,矩形 中, , ,点 从点 出发,沿 向终点 匀速运动,设点 走过的路程为 , 的面积为 ,能符合题意反映 与 之间函数关系的图象是( )
A、OA=OC,AD∥BC B、∠ABC=∠ADC,AD∥BC C、AB=DC,AD=BC D、∠ABD=∠ADB,∠BAO=∠DCO6. 如图,矩形 中, , ,点 从点 出发,沿 向终点 匀速运动,设点 走过的路程为 , 的面积为 ,能符合题意反映 与 之间函数关系的图象是( )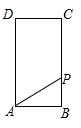 A、
A、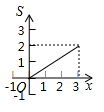 B、
B、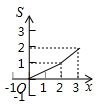 C、
C、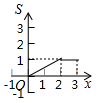 D、
D、
二、填空题
-
7. 函数 中自变量x的取值范围是.8. 将直线y=2x+1向下平移3个单位长度后所得直线的表达式是 .9. 如图所示,矩形ABCD两条对角线夹角为60°,AB=2,则对角线AC长为 .
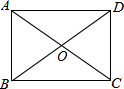 10. 已知一组数据1,5,7,x的众数与中位数相等,则这组数据的平均数是 .11. 观察下列各式:
10. 已知一组数据1,5,7,x的众数与中位数相等,则这组数据的平均数是 .11. 观察下列各式:,
,
,
……
请利用你所发现的规律,
计算 + + +…+ ,其结果为 .
12. 在△ABC 中,∠A=30°,∠B=90°,AC=8,点 D 在边 AB, 且 BD= ,点 P 是△ABC 边上的一个动点,若 AP=2PD 时,则 PD的长是 .三、解答题
-
13.(1)、计算:(2)、已知 , ,求 的值14. 在 中, , , .试判断 的形状.15. 如图,平行四边形ABCD中,AE=CE , 请仅用无刻度的直尺完成下列作图:
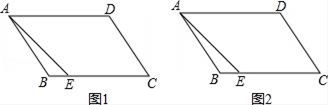 (1)、在图1中,作出∠DAE的角平分线;(2)、在图2中,作出∠AEC的角平分线.16. 如图,在平面直角坐标系中,直线AC与x轴交于C点,与y轴交于A点,直线AB与x轴交于B点,与y轴交于A点,已知A(0,4),B(2,0).
(1)、在图1中,作出∠DAE的角平分线;(2)、在图2中,作出∠AEC的角平分线.16. 如图,在平面直角坐标系中,直线AC与x轴交于C点,与y轴交于A点,直线AB与x轴交于B点,与y轴交于A点,已知A(0,4),B(2,0).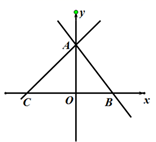 (1)、求直线AB的解析式;(2)、若 ,求点C的坐标.17. 如图,四边形 是菱形,对角线 cm, cm, 于 ,求 的长.
(1)、求直线AB的解析式;(2)、若 ,求点C的坐标.17. 如图,四边形 是菱形,对角线 cm, cm, 于 ,求 的长.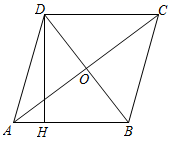 18. 中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校5000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
18. 中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校5000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:频数频率分布表:
成绩x(分)
频数(人)
频率
50≤x<60
10
0.05
60≤x<70
30
0.15
70≤x<80
40
b
80≤x<90
a
0.35
90≤x≤100
50
0.25
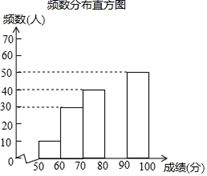
根据所给信息,解答下列问题:
(1)、a= , b= ;(2)、补全频数分布直方图;(3)、这200名学生成绩的中位数会落在分数段;(4)、若成绩在70分以上(包括70分)为“合格”等,请你估计该校参加本次比赛的5000名学生中成绩是“合格”的约有多少人?19. 已知函数 ,点 在其图像上.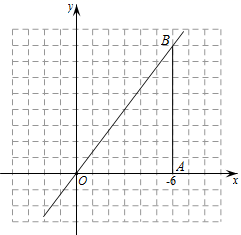 (1)、求a的值;(2)、过点 作 轴于 点,求 的长;(3)、在条件(2)下,点 在线段 上,将线段 沿直线 翻折,使点 落在 上的 点处,求 所在直线的解析式.20. 为传承红色基因,引导学生学党史、知党情、感党恩,培养爱国情怀,某校开展了红色研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生,现有甲、乙两种大客车,它们的载客量和租金如下表所示,为了安全既要保证所有师生都有车坐,又要保证每辆车上至少要有2名老师.
(1)、求a的值;(2)、过点 作 轴于 点,求 的长;(3)、在条件(2)下,点 在线段 上,将线段 沿直线 翻折,使点 落在 上的 点处,求 所在直线的解析式.20. 为传承红色基因,引导学生学党史、知党情、感党恩,培养爱国情怀,某校开展了红色研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生,现有甲、乙两种大客车,它们的载客量和租金如下表所示,为了安全既要保证所有师生都有车坐,又要保证每辆车上至少要有2名老师.甲种客车
乙种客车
载客量(人/辆)
30
42
租金(元/辆)
300
400
(1)、参加此次研学旅行活动的老师和学生各有多少人?(2)、设租用两种车共8辆,其中 辆甲种客车,租车总费用为 元,学校计划此次研学旅行活动的租车总费用不超过3100元,且保证师生都有座位,怎样租车最省钱?请说明理由.21. 如图1,菱形 的对角线 、 相交于点 ,且 cm , cm , 分别过点 、 作 与 的平行线相交于点 .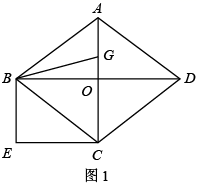
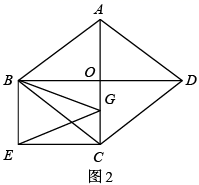 (1)、判断四边形 的形状并证明;(2)、点 从点 沿线段 的方向以2cm/s的速度移动了 秒,连接 ,当 时,求 的值.(3)、如图2,点 在直线 上运动,求 的最小值.22. 模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)、判断四边形 的形状并证明;(2)、点 从点 沿线段 的方向以2cm/s的速度移动了 秒,连接 ,当 时,求 的值.(3)、如图2,点 在直线 上运动,求 的最小值.22. 模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下: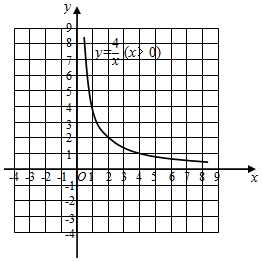 (1)、建立函数模型
(1)、建立函数模型设矩形相邻两边的长分别为x,y,由矩形的面积为4,得 ,即 ;由周长为m,得 ,即 .满足要求的 应是两个函数图象在第象限内交点的坐标.
(2)、画出函数图象函数 的图象如图所示,而函数 的图象可由直线 平移得到.请在同一直角坐标系中直接画出直线 .
(3)、平移直线 ,观察函数图象①当直线平移到与函数 的图象有唯一交点 时,周长m的值为 ▲ ;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
(4)、得出结论若能生产出面积为4的矩形模具,则周长m的取值范围为 .
23. 如图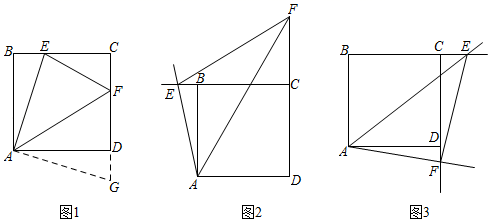 (1)、(发现证明)
(1)、(发现证明)如图1,在正方形ABCD中,点E , F分别是BC , CD边上的动点,且∠EAF=45°,求证:EF=DF+BE .
小明发现,当把△ABE绕点A顺时针旋转90°至△ADG , 使AB与AD重合时能够证明,请你给出证明过程.
(2)、(类比引申)①如图2,在正方形ABCD中,如果点E , F分别是CB , DC延长线上的动点,且∠EAF=45°,则(1)中的结论还成立吗?请写出证明过程.②如图3,如果点E , F分别是BC , CD延长线上的动点,且∠EAF=45°,则EF , BE , DF之间的数量关系是 ▲ (不要求证明)
(3)、(联想拓展)如图1,若正方形ABCD的边长为6,AE=3 ,求AF的长.