广东省江门市2020-2021学年高二下学期数学期末考试试卷
试卷更新日期:2021-08-09 类型:期末考试
一、单选题
-
1. 复数 的共轭复数是( )A、 B、 C、 D、2. “ ”是“曲线 表示椭圆”的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件3. 已知椭圆 的左右焦点分别为 , ,离心率为 ,过 的直线 交 于 两点,若 的周长为 则,椭圆 的方程为( )A、 B、 C、 D、4. 与直线 关于 轴对称的直线的方程为( )A、 B、 C、 D、5. 意大利著名天文学家伽利略曾错误地猜测链条自然下垂时的形状是抛物线.直到1690年,雅各布·伯努利正式提出该问题为“悬链线”问题并向数学界征求答案.1691年他的弟弟约翰·伯努利和菜布尼兹、惠更斯三人各自都得到了正确答案,给出悬链线的数学表达式——双曲余弦函数: ( 为自然对数的底数).当 , 时,记 , , ,则 , , 的大小关系为( ).
 A、 B、 C、 D、6. 已知双曲线的渐近线为 ,且过点 ,则该双曲线的标准方程为( )A、 B、 C、 D、7. 棱长均为3的三棱锥 ,若空间一点 满足 ,则 的最小值为( )A、 B、 C、 D、18. 如果 , ,…, 是抛物线C: 上的点,它们的横坐标依次为 , ,…, ,点F是抛物线C的焦点.若 =10, =10+n , 则p等于( )A、2 B、 C、 D、4
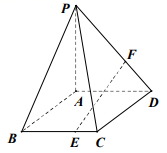
A、 B、 C、 D、6. 已知双曲线的渐近线为 ,且过点 ,则该双曲线的标准方程为( )A、 B、 C、 D、7. 棱长均为3的三棱锥 ,若空间一点 满足 ,则 的最小值为( )A、 B、 C、 D、18. 如果 , ,…, 是抛物线C: 上的点,它们的横坐标依次为 , ,…, ,点F是抛物线C的焦点.若 =10, =10+n , 则p等于( )A、2 B、 C、 D、4二、多选题
-
9. 已知 , 是两条不重合的直线, , , 是三个两两不重合的平面,则下列命题正确的是( )A、若 , , ,则 B、若 , ,则 C、若 , , ,则 D、若 , ,则10. 定义:以双曲线的实轴为虚轴,虚轴为实轴的双曲线与原双曲线互为共轭双曲线.以下关于共轭双曲线的结论正确的是( )A、与 共轭的双曲线是 B、互为共轭的双曲线渐近线不相同 C、互为共轭的双曲线的离心率为 、 则 D、互为共轭的双曲线的 个焦点在同一圆上11. 如图,在棱长为1的正方体 中,点 在线段 上运动,则下列判断中正确的是( )
 A、三棱锥 的体积是 B、 平面 C、平面 与平面 所成的二面角为 D、异面直线 与 所成角的范围是12. 已知函数 ,则下列结论正确的是( )A、 是以 为周期的函数 B、 是奇函数 C、 在 上为增函数 D、 在 内有20个极值点
A、三棱锥 的体积是 B、 平面 C、平面 与平面 所成的二面角为 D、异面直线 与 所成角的范围是12. 已知函数 ,则下列结论正确的是( )A、 是以 为周期的函数 B、 是奇函数 C、 在 上为增函数 D、 在 内有20个极值点三、填空题
-
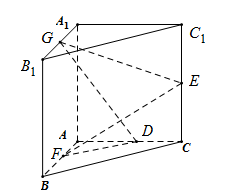
13. 命题“ , ”的否定是 .14. 已知复数z与 (z +2)2-8i 均是纯虚数,则 z = .15. 过点 的直线与圆 相交于 、 两点,则 的最小值为 .16. 如图,在直三棱柱 中, , ,已知 和 分别为 和 的中点, 和 分别为线段 和 上的动点(不包括端点),若 ,则线段 长度的取值范围为 .
四、解答题
-
17. 已知抛物线 的焦点为 ,并且经过点 .(1)、求抛物线 的方程;(2)、过原点 作倾斜角为45°的直线 交抛物线 于 , 两点,求 的面积.18. 已知空间三点 , , .(1)、求 的面积;(2)、若向量 ,且 ,求向量 的坐标.19. 已知函数 .(1)、当 时,求 在 处的切线方程;(2)、若 在区间 上的极小值为 ,求它在该区间上的最大值.