江西省赣州市赣县区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-08-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{32}$ B、 $\sqrt{5}$ C、 $\sqrt{\frac{4}{3}}$ D、 $\sqrt{1.5}$

查看试题解析
2. 下列各组数中，以它们为边长的线段能构成直角三角形的是（）

A、2，4，4 B、 $\sqrt{2}$ ，2，2 C、3，4，5 D、5，12，14

查看试题解析
3. 某公司有10名员工，每人年收入数据如下表：

年收入/万元

4

6

8

10

人数/人

3

4

2

1

则他们年收入数据的众数与中位数分别为（）

A、4，6 B、6，6 C、4，5 D、6，5

查看试题解析
4. 对于函数y=2x﹣1，下列说法正确的是（）

A、它的图象过点（1，0） B、y值随着x值增大而减小 C、它的图象经过第二象限 D、当x＞1时，y＞0

查看试题解析
5. 如图，在正方形 $A B C D$ 的外侧，作等边 $Δ A B E$ ，则 $∠ B E D$ 为（）

A、 $15 °$ B、 $45 °$ C、 $55 °$ D、 $60 °$

查看试题解析
6. 如图是由三个全等的菱形拼接成的图形，若平移其中一个菱形，与其他两个菱形重新拼接（无覆盖，有公共顶点），并使拼接成的图形为轴对称图形，则平移的方式共有（）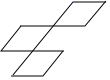

A、3种 B、6种 C、8种 D、10种

查看试题解析

二、填空题

7. 若式子 $\sqrt{x + 2}$ 有意义，则x的取值范围是．

查看试题解析
8. 如图，点E在正方形ABCD的边AB上，若EB=1，EC=2，那么正方形ABCD的面积为.

查看试题解析
9. 某校女子排球队队员的年龄分布如下表：
年龄
13
14
15
人数
4
7
4
则该校女子排球队队员的平均年龄是岁．

查看试题解析
10. $Δ A B C$ 中，点 $D$ ， $E$ 分别是 $Δ A B C$ 的边 $A B$ ， $A C$ 的中点，连接 $D E$ ．若 $∠ C = 68 °$ ，则 $∠ A E D =$

查看试题解析
11. 2021年5月22日，在甘肃省白银市景泰县黄河石林景区举行了黄河石林山地马拉松百公里越野赛．如图，是矗立在水平地面上的马拉松赛道路牌．经测量得到以下数据：AC＝4 m， $B E = 8 \sqrt{3}$ m，∠DAC＝45°，∠EBC＝30°，∠DCA＝90°，则路牌的高DE为m

查看试题解析
12. 在平面直角坐标系xOy中，已知点A（7，0），B（0，4），C（7，4），连接AC，BC得到矩形AOBC，点D在边BC上，将边OB沿OD折叠，点B的对应点为B′，若点B′到矩形较长两对边的距离之比为1：3，则BB′= ．

查看试题解析

三、解答题

13.

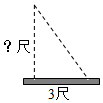
(1)、计算： $\sqrt{24} \times 4 \sqrt{\frac{1}{2}} \div \sqrt{48}$

(2)、我国古代数学著作《九章算术》中有这样一个问题：“今有竹高一丈，末折抵地，去本三尺，问折者高几何？”意即：一根竹子高1丈，折断后竹子顶端落在离竹子底端3尺处．求折断处离地面的高度（注：其中的丈、尺是长度单位，1丈 $= 10$ 尺）

查看试题解析
14. 如图，在平行四边形 $A B C D$ 中， $A B = 10$ ， $A D = 8$ ， $A C ⊥ B C$ ．求△BOC的面积．

查看试题解析
15. 已知一次函数的图象经过点 $(3 ， 1)$ 和 $(0 ， - 2)$ .

(1)、求该函数图象与x轴的交点坐标；

(2)、判断点 $(- 3 ， 6)$ 是否在该函数图象上.

查看试题解析
16. 如图，已知正方形ABCD ，请仅用无刻度的直尺，分别按照下列要求作图．（保留作图痕迹，不写作法）．

(1)、如图（1），若点E在AD边上，连接BE ，请作出 $▱$ BEDF；

(2)、如图（2），若点E在正方形ABCD的对角线AC上，请以BE ， DE为边作一个菱形．

查看试题解析
17. 某学校从八年级同学中任意选取40人，随机分成甲、乙两个小组进行“引体向上”体能测试．根据测试成绩绘制出下面的统计表和如图的统计图．已知甲组的平均成绩为8.7分．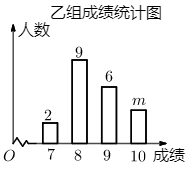

甲组成绩统计表：

成绩

7

8

9

10

人数

1

9

5

5

请根据上面的信息，解答下列问题：

(1)、m= ，甲组成绩的中位数是，乙组成绩的众数是；

(2)、参考下面甲组成绩方差的计算过程，求乙组成绩的方差，并判断哪个小组的成绩更加稳定？
$S_{甲}^{2} = \frac{1 \times {(7 - 8.7)}^{2} + 9 \times {(8 - 8.7)}^{2} + 5 {(9 - 8.7)}^{2} + 5 \times {(10 - 8.7)}^{2}}{20} = 0.81$

查看试题解析

18. 为推进“不忘初心，牢记使命”主题教育活动，某区对学校教师在“学习强国”APP上的学习时间进行了抽样调查，过程如下．

收集数据

从全区随机抽取20名教师，调查平均每天在“学习强国”APP上的学习时间（单位：min），数据如下．

79 85 73 80 75 76 87 70 75 94

75 79 81 71 75 80 86 69 83 77

整理数据

按下表分段整理样本数据．

学习时间x/min	60≤x≤69	70≤x≤79	80≤x≤89	90≤x≤100
等级	D	C	B	A
人数	1	a	7	1

分析数据

样本数据的平均数、众数及中位数如下表．（单位：min）

平均数	众数	中位数
78.5	b	c

处理数据

(1)、填空：a＝， b＝， c＝．

(2)、若该区共有3000名教师，请估计该区教师平均每天在“学习强国”APP上的学习时间处于B等级及以上的人数．

(3)、假设在“学习强国”APP上学习时间的三分之一是用来阅读文章的，平均阅读一篇文章耗时5min，请你选择样本中的“平均数或众数或中位数”估计该区教师每人一年（按365天计算）平均阅读文章的篇数．

查看试题解析

19. 我国是世界上水资源最缺乏的国家之一，同时又有很多水龙头由于漏水造成大量的浪费.某校园内有一个漏水的水龙头，数学活动小组用最大容量为200毫升的量筒接水，每隔10秒钟观察量筒中水的体积，从某一时刻起记录1分钟内量筒中水的体积如下表（精确到 $1 m l$ ）：

时间 $t (s)$

10

20

30

40

50

60

量筒中的水量 $V (m l)$

30

45

60

75

90

105

(1)、在平面直角坐标系中描出表中数据对应的点；

(2)、量筒中的水量 $V (m l)$ 是否为时间 $t (s)$ 的函数？如果是，试求出一个符合表中数据的函数解析式；

(3)、若水费为3.6元/ $m^{3}$ ，按这样的漏水速度，这个水龙头一个月（30天）要浪费多少钱？（ $1 m^{3} = 10^{6} m l$ ，结果保留整数）.

查看试题解析
20. 如图

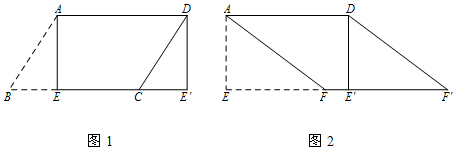(1)、如图1，在平行四边形纸片ABCD中， $A D = 5$ ， $S_{▱ A B C D} = 15$ ，过点 $A$ 作 $A E ⊥ B C$ ，垂足为 $E$ ，沿 $A E$ 剪下 $Δ A B E$ ，将它平移至 $Δ D C E^{'}$ 的位置，拼成四边形 $A E E^{'} D$ ，试判断四边形 $A E E^{'} D$ 是什么特殊四边形，并说明理由．

(2)、如图2，在（1）中的四边形纸片 $A E E^{'} D$ 中，在 $E E^{'}$ 上取一点 $F$ ，使 $E F = 4$ ，剪下 $Δ A E F$ ，将它平移至△ $D E^{'} F^{'}$ 的位置，拼成四边形 $A F F^{'} D$ ．
①求证：四边形 $A F F^{'} D$ 是菱形；

②求四边形 $A F F^{'} D$ 的两条对角线的长．

查看试题解析
21. 如图，在平面直角坐标系中，边长为2的正方形 $A B C D$ 在第一象限内， $A D / / y$ 轴，点A的坐标为 $(5 ， 3)$ ，已知直线 $l ： y = \frac{1}{2} x - 2$ ．

(1)、将直线l向上平移m个单位，使平移后的直线恰好经过点A ，求m的值；

(2)、在（1）的条件下，平移后的直线与正方形的边长 $B C$ 交于点E ，求 $△ A B E$ 的面积．

查看试题解析
22. 定义：一组邻边相等且对角互补的四边形叫做“等补四边形”
如图1，四边形ABCD中，AD＝CD ， ∠A+∠C＝180°，则四边形ABCD叫做“等补四边形”．

(1)、概念理解
①在以下四种图形中，一定是“等补四边形”的是（）

A ．平行四边形 B ．菱形 C ．矩形 D ．正方形

②等补四边形ABCD中，若∠B∶∠C∶∠D＝2∶3∶4，则∠A＝；

(2)、知识运用
如图1，在四边形ABCD中，BD平分∠ABC ， AD＝CD ， BC＞BA ．求证：四边形ABCD是等补四边形

(3)、探究发现
如图2，在等补四边形ABCD中，AB＝AD ，连接AC ， AC是否平分∠BCD？请说明理由．

查看试题解析
23. 如图，在平面直角坐标系中，直线 $y = x + 2$ 与 $x$ 轴、 $y$ 轴分别交 $A$ 、 $B$ 两点，与直线 $y = - \frac{1}{2} x + b$ 相交于点 $C (2 ， m)$ ，

(1)、求点 $A$ 、 $B$ 的坐标；

(2)、求 $m$ 和 $b$ 的值；

(3)、若直线 $y = - \frac{1}{2} x + b$ 与 $x$ 轴相交于点 $D$ ．动点 $P$ 从点 $D$ 开始，以每秒 $1$ 个单位的速度向 $x$ 轴负方向运动，设点 $P$ 的运动时间为 $t$ 秒，
①若点 $P$ 在线段 $D A$ 上，且 $Δ A C P$ 的面积为 $10$ ，求 $t$ 的值；

②是否存在 $t$ 的值，使 $Δ A C P$ 为等腰三角形？若存在，求出 $t$ 的值；若不存在，请说明理由．

查看试题解析

时间 $t (s)$	10	20	30	40	50	60
量筒中的水量 $V (m l)$	30	45	60	75	90	105

年收入/万元	4	6	8	10
人数/人	3	4	2	1

年龄	13	14	15
人数	4	7	4

成绩	7	8	9	10
人数	1	9	5	5