福建省泉州市泉港区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-08-09 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 × = B、 + = C、 =4 D、 ﹣ =2. 用配方法解方程 .下列配方结果正确的是( )A、 B、 C、 D、3. 某一芯片实现国产化后,经过两次降价,每块芯片单价由188元降为108元.若两次降价的百分率相同,设每次降价的百分率为 ,根据题意列方程得( )A、 B、 C、 D、4. 已知点 与点 关于原点对称,则点 的坐标( )A、 B、 C、 D、5. 若点 在一次函数 的图象上,则点 一定不在( )A、第四象限 B、第三象限 C、第二象限 D、第一象限6. 同时掷两枚普通的正方体骰子,下列事件属于不可能事件的是( )A、两枚骰子的点数和为12 B、两枚骰子的点数和为6 C、两枚骰子的点数和为奇数 D、两枚骰子的点数和为17. 已知 的周长为56, ,则 的长为( )A、18 B、23 C、36 D、468. 下列结论中,矩形具有而菱形不一定具有的性质是( )A、内角和为360° B、对角线互相平分 C、对角线相等 D、对角线互相垂直9. 如图,点 是矩形 内一点, , .下列错误的是( )
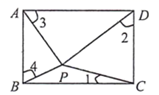 A、 B、 C、 D、10. 已知点 、 在反比例函数 的图象上,且 、 ,则 的取值范围是( )A、 B、 C、 D、 或
A、 B、 C、 D、10. 已知点 、 在反比例函数 的图象上,且 、 ,则 的取值范围是( )A、 B、 C、 D、 或二、填空题
-
11. 在函数 中,自变量 的取值范围是 .12. 计算 的结果等于 .13. 若 、 是方程 的两根,则x1+x2=.14. 某校为了解学生的近视情况,对学生进行普查,统计结果绘制如下表,若随机抽取一名学生,则抽中近视的学生的概率为.
年级
七年级
八年级
九年级
总学生数
325
269
206
近视的学生数
195
156
89
15. 四边形 中, ,对角线 、 相交于点 , 于点 , 于点 ,连接 、 ,当 时,以下四个结论:① ;② ;③四边形 是菱形:④ .其中正确的个数是.16. 已知 是正整数,关于 的方程 有正整数根,则方程的解为:.三、解答题
-
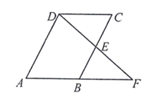
17. 计算: .18. 如图,点 是 边 上的中点,连结 并延长交 的延长线于点 .求证: .
 19. 矩形纸片的长和宽分别为 、 ,在纸片的四个角都剪去一个边长为 的正方形.
19. 矩形纸片的长和宽分别为 、 ,在纸片的四个角都剪去一个边长为 的正方形. (1)、请画出图形,并用含有 , , 的代数式表示纸片剩余部分的面积;(2)、当 ,剩余部分的面积恰好等于剪去面积的4倍时,求纸片的长与宽.20. 经过点 的直线 与直线 相交于点 .
(1)、请画出图形,并用含有 , , 的代数式表示纸片剩余部分的面积;(2)、当 ,剩余部分的面积恰好等于剪去面积的4倍时,求纸片的长与宽.20. 经过点 的直线 与直线 相交于点 .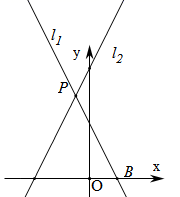 (1)、请求 的值;(2)、试求出 的长度.21. 如图,已知 、 分别是正方形 边 、 边上的动点, , .
(1)、请求 的值;(2)、试求出 的长度.21. 如图,已知 、 分别是正方形 边 、 边上的动点, , . (1)、求证: ;(2)、设 的面积为 , 的长为 .试求出 与 之间的函数表达式.22. 如图, 中, , ,点 是边 的中点.
(1)、求证: ;(2)、设 的面积为 , 的长为 .试求出 与 之间的函数表达式.22. 如图, 中, , ,点 是边 的中点.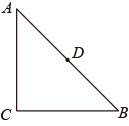 (1)、求作一点 ,使得点 与点 关于 对称;(要求:尺规作图,保留痕迹,不写作法)(2)、连接 ,请写出线段 、 之间的关系,并证明.23. 首届国家最高科学技术奖得主,被誉为“杂交水稻之父”袁隆平带领团队选育出超优1000、 两优900、准两优527等超级稻品种屡创产量新高,保障国家粮食安全做出了杰出贡献,更为世界和平和社会进步树立了丰碑.为了解种植户播种的满意度,有关部门从种植户中随机抽取100户作为样本,整理后得到下表数据:
(1)、求作一点 ,使得点 与点 关于 对称;(要求:尺规作图,保留痕迹,不写作法)(2)、连接 ,请写出线段 、 之间的关系,并证明.23. 首届国家最高科学技术奖得主,被誉为“杂交水稻之父”袁隆平带领团队选育出超优1000、 两优900、准两优527等超级稻品种屡创产量新高,保障国家粮食安全做出了杰出贡献,更为世界和平和社会进步树立了丰碑.为了解种植户播种的满意度,有关部门从种植户中随机抽取100户作为样本,整理后得到下表数据:满意度
(得分)
大面积种植户
小面积种植户
超优1000
两优900
准两优527
超优1000
两优900
准两优527
满意(100)
25
20
11
11
12
11
一般(80)
2
3
2
2
0
1
(1)、在样本中任抽2位种植户,若抽到种植超优1000、 两优900、准两优527的种植户机会是相同的.请用树状图或列表法求出抽到播种不同品种超级稻的概率;(2)、玉米种植户李伯伯欲将一些玉米地改为播种水稻.如果以满意度的平均值作为决策依据,应该选择哪一品种超级稻?请说明理由.24. 如图,在 中, ,过点 作 交 的延长线于点 .已知 , ,点 是射线 上一动点,把 沿 折叠,点 的对应点为点 .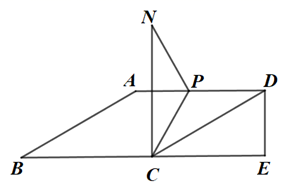 (1)、请求出 的度数;(2)、当 时,试求出 的长度;(3)、当 时,试求出 的长度.25. 点 为平面直角坐标系的原点,点 、 在反比例函数 的图象上,点 、 在反比例函数 的图象上,且 .
(1)、请求出 的度数;(2)、当 时,试求出 的长度;(3)、当 时,试求出 的长度.25. 点 为平面直角坐标系的原点,点 、 在反比例函数 的图象上,点 、 在反比例函数 的图象上,且 . (1)、若点 的坐标为 ,点 恰好为 的中点,过点 作 轴于点 ,交 的图象于点 .
(1)、若点 的坐标为 ,点 恰好为 的中点,过点 作 轴于点 ,交 的图象于点 .①请求出 、 的值;
②试求 的面积.
(2)、若 轴, , 与 间的距离为6,试说明 的值是否为某一固定值?如果是定值,试求出这个定值;若不是定值,请说明理由.