福建省莆田市涵江区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各组数中能作为直角三角形的三边长的是（　　）

A、1，2，3 B、3，4，5 C、4，5，6 D、7，8，9

查看试题解析
2. 估计 $\sqrt{38}$ 的值在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{9} = \sqrt{11}$ B、 $3 \sqrt{2} - \sqrt{2} = 2 \sqrt{2}$ C、 $\sqrt{5} \times \sqrt{4} = 4 \sqrt{5}$ D、 $\sqrt{3} \times \frac{1}{\sqrt{3}} = \frac{1}{3}$

查看试题解析
4. 在某校举行的“我的中国梦”演讲比赛中，有5名学生参加决赛，他们决赛的最终成绩各不相同，其中的一名学生要想知道自己能否进入前3名，不仅要了解自己的成绩，还要了解这5名学生成绩的（）

A、众数 B、方差 C、中位数 D、平均数

查看试题解析
5. 将直线 $y = 3 x$ 沿 $y$ 轴向下平移1个单位长度后得到的直线解析式为（）

A、 $y = 3 x + 3$ B、 $y = 3 x - 3$ C、 $y = 3 x + 1$ D、 $y = 3 x - 1$

查看试题解析
6. 下列判断错误的是（　　）

A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、四条边都相等的四边形是菱形 D、两条对角线垂直且平分的四边形是正方形

查看试题解析
7. 如图，广场中心菱形花坛 $A B C D$ 的周长是32米， $∠ A = 60 °$ ，则 $A$ 、 $C$ 两点之间的距离为（）

A、4米 B、4 $\sqrt{3}$ 米 C、8米 D、8 $\sqrt{3}$ 米

查看试题解析
8. 如图是一次函数y₁=kx+b与y₂=x+a的图象，则下列结论中错误的是（）

A、k＜0 B、a＞0 C、b＞0 D、方程kx+b=x+a的解是x=3

查看试题解析
9. 如图，点 $E$ 在矩形 $A B C D$ 的边 $D C$ 上， $△ A D E$ 沿直线 $A E$ 折叠，使点 $D$ 落在 $B C$ 边上的点 $F$ 处，已知 $A B = 3$ ， $B F = 4$ ，则 $C E$ 的长等于（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{5}{3}$ D、 $\frac{3}{5}$

查看试题解析
10. 甲、乙两车从A地出发，匀速驶向B地，甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶，乙车先到达B地并停留1h后，再以原速沿原路返回，直至与甲车相遇。在此过程中，两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示。下列说法错误的是（）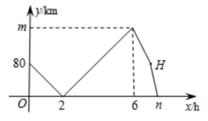

A、乙车的速度是120km/h B、m=160 C、点H的坐标是(7，80) D、n=7.5

查看试题解析

二、填空题

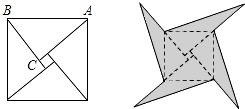
11. 甲、乙两组数据的平均数相等，甲组数据的方差 $S_{甲}^{2} = 0.050$ ，乙组数据的方差 $S_{乙}^{2} = 0.055$ ，则数据波动较大的是组.

查看试题解析
12. 若 $x = \sqrt{2} - 1$ ， $y = \sqrt{2} + 1$ ，则 $x^{2} y + x y^{2} =$ .

查看试题解析
13. 小明在计算方差时，使用公式 $S^{2} = \frac{1}{4} [{(2 - \bar{x})}^{2} + {(3 - \bar{x})}^{2} + {(3 - \bar{x})}^{2} + {(8 - \bar{x})}^{2}]$ ，则公式中的 $\bar{x} =$ .

查看试题解析
14. 如图是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若 $A C = 6$ ， $B C = 5$ ，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到如图所示的“数学风车”，则这个风车的外围周长是．

查看试题解析
15. 如图， $▱ A B C D$ 中， $∠ B C D$ 和 $∠ A B C$ 的平分线分别交 $A D$ 于 $E$ 、 $F$ 两点， $C E$ 、 $B F$ 交于点 $G$ ，若 $A B = 3$ ， $B C = 4$ ，则 $E G^{2} + F G^{2} =$ .

查看试题解析
16. 如图，已知直线 $y = \frac{3}{4} x + 4$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ， $P$ 为线段 $A B$ 上的个动点，过点 $P$ 分别作 $P F ⊥ x$ 轴于点 $F$ ， $P E ⊥ y$ 轴于点 $E$ ，连接 $E F$ ，则 $E F$ 长的最小值为.

查看试题解析

三、解答题

17. 计算： $\sqrt{12} - \sqrt{6} \div \sqrt{2} + {(1 - \sqrt{3})}^{2}$ .

查看试题解析
18. 已知：如图，E，F为平行四边形ABCD的对角线BD上的两点，且 $B E = D F$ ，求证： $A E ∥ C F$ .

查看试题解析
19. 已知直线 $l_{1}$ 和 $l_{2}$ 的表达式分别为 $y = 2 x - 3$ 和 $y = k x - 5$ ，这两条直线相交于点 $A$ $(- 2$ ， $n)$ .

(1)、求 $n$ 和 $k$ 的值；

(2)、若直线 $l_{3}$ 的表达式为 $y = - 6 x - 19$ ，试说明：直线 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 相交于同一个点.

查看试题解析
20. 如图，已知 $△ A B C$ .

(1)、请用直尺和圆规确定一点 $D$ ，使得四边形 $A B C D$ 是平行四边形；(保留作图痕迹，不写作法)

(2)、根据你的作图，证明四边形 $A B C D$ 是平行四边形.

查看试题解析
21. 端午假期刚过，集美龙舟队有开始新的一轮训练，为更加有效训练队员，集美龙舟队决定公开招聘教练，经过笔试后筛选出甲、乙两位教练进行面试和体侧，两人的成绩如下表.

体侧

面试

甲

90

88

乙

84

92

(1)、当体侧成绩权重为6，面试成绩权重为4，请问甲、乙两人谁的成绩高？

(2)、当体侧成绩权重为 $a$ ，面试和体侧各有权重，并且权总和为10，请问当 $a$ 取什么范围，乙成绩比甲高？

查看试题解析

22. 有这样一个问题：探究函数

y = | x - 1 |

的图象与性质.小华根据学习函数的经验，对函数

y = | x - 1 |

的图象与性质进行了探究.下面是小华的探究过程，请补充完整：

(1)、在函数

y = | x - 1 |

中，自变量x的取值范围是 ▲ .

x	…	-4	-3	-2	-1	0	1	2	3	4	…
y	…	5	4	3	2	1	0	1	2	m	…

①求m的值；

②在平面直角坐标系xOy中，描出以上表中各组对应值为坐标的点，并根据描出的点，画出该函数的图象.

(2)、结合函数图象写出该函数的一条性质：.

查看试题解析

23. 某公司招聘外卖送餐员，送餐员的月工资由底薪1000元加上外卖送单补贴

(

送一次外卖称为一单

)

构成，外卖送单补贴的具体方案如下：

外卖送单数量	补贴 $($ 元 $/$ 单 $)$
每月不超过500单	6
超过500单但不超过m单的部分 $(700 \leq m \leq 900)$	8
超过m单的部分	10

(1)、若某“外卖小哥”4月份送餐400单，则他这个月的工资总额为多少元？

(2)、设5月份某“外卖小哥”送餐x单

(x > 500)

，所得工资为y元，求y与x的函数关系式.

(3)、若某“外卖小哥”5月份送餐800单，所得工资为6500元，求m的值.

查看试题解析

24. 如图，在矩形ABCD中，AD＝nAB，E，F分别在AB，BC上．

(1)、若n＝1，AF⊥DE．
①如图1，求证：AE＝BF；

②如图2，点G为CB延长线上一点，DE的延长线交AG于H，若AH＝AD，求证：AE+BG＝AG；

(2)、如图3，若E为AB的中点，∠ADE＝∠EDF．则 $\frac{C F}{B F}$ 的值是（结果用含n的式子表示）．

查看试题解析
25. 如图在平面直角坐标系中，直线 $y = \frac{1}{2} x + m$ 分别交 $x$ 轴， $y$ 轴于 $A$ 、 $B$ 两点，点 $A$ 的坐标为 $(- 2 ， 0)$ ，且点 $C$ 的坐标为 $(3 ， 0)$ .

(1)、求点 $B$ 坐标；

(2)、若点 $B$ 、 $C$ 关于直线 $l$ 对称，在备用图中画出直线 $l$ ，再求直线 $l$ 的函数解析式；

(3)、点 $M$ 是直线 $y = x + m$ 与直线l的交点，点 $N$ 在第一象限内，当 $△ B M N$ 为等腰直角三角形时，直接写出点 $N$ 的坐标.

查看试题解析

	体侧	面试
甲	90	88
乙	84	92