福建省龙岩市新罗区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-09 类型：期末考试

进入出卷网下载

一、单选题

1. 函数 $y = \sqrt{2 x + 6}$ 中自变量x的取值范围是（）

A、x＜ $- 3$ B、x≥ $- 3$ C、x≤ $- 3$ D、x＞ $- 3$

查看试题解析
2. 化简 $\sqrt{25 \frac{1}{4}}$ 等于（）

A、 $\frac{5}{2}$ B、 $5 \frac{1}{2}$ C、 $\frac{1}{2} \sqrt{101}$ D、 $\pm \frac{\sqrt{101}}{2}$

查看试题解析
3. 甲、乙、丙、丁四位同学在三次数学测验中，他们成绩的平均分是x_甲＝85，x_乙＝85，x_丙＝85，x_丁＝85，方差是s_甲²＝3.8，s_乙²＝2.3，s_丙²＝6.2，s_丁²＝5.2，则成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 在一次数学测验中，一学习小组七人的成绩如图所示，则这七人成绩的中位数是（）

成绩

70

89

96

100

人数

1

2

3

1

A、22 B、89 C、92 D、96

查看试题解析
5. 如图，公路 $A C$ ， $B C$ 互相垂直，公路 $A B$ 的中点 $M$ 与点 $C$ 被湖隔开.测得 $A B$ 的长为 $1.6 k m$ ，则 $M ， C$ 两点间的距离为（）

A、 $0.5 k m$ B、 $0.6 k m$ C、 $0.8 k m$ D、 $1.2 k m$

查看试题解析
6. 下列条件中，能判定四边形是菱形的是（）

A、两组对边分别相等 B、两条对角线互相平分且相等 C、两条对角线相等且互相垂直 D、两条对角线互相垂直平分

查看试题解析
7. 两只小鼹鼠在地下从同一处开始打洞，一只朝北面挖，每分钟挖8cm，另一只朝东面挖，每分钟挖6cm，10分钟之后两只小鼹鼠相距（）

A、100cm B、50cm C、140cm D、80cm

查看试题解析
8. 已知一次函数y=kx+b（k≠0）图象经过第二、三、四象限，则一次函数y=﹣bx+kb图象可能是（）

A、 B、 C、 D、

查看试题解析
9. 如图，在▱ABCD中，点E在边AD上，以BE为折痕，将△ABE向上翻折，点A正好落在CD上的点F，若△FDE的周长为8，△FCB的周长为22，则FC的长为（）

A、15 B、7 C、14 D、8

查看试题解析
10. 如图，点A、B、C在一次函数y＝﹣2x+m的图象上，它们的横坐标依次为﹣1、1、2，分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积的和是（）.

A、3 B、3.6 C、4.8 D、6

查看试题解析

二、填空题

11. 一次函数y=2x+4的图象与y轴交点的坐标是．

查看试题解析
12. 长方形的宽是 $\sqrt{3}$ ，面积为 $2 \sqrt{6}$ ，则长方形的长为

查看试题解析
13. 菱形的对角线长分别为6和8，则此菱形的面积为．

查看试题解析
14. 在某中学举行演讲比赛中，评委组的各位评委给小明同学的演讲打分情况如下表，则小明同学平均得分是.

分数（分）

91

92

93

94

95

评委（位）

1

2

1

2

1

查看试题解析
15. 如图，已知一次函数y＝kx+b的图象经过点（3，0），则当函数值y小于0时，自变量x的取值范围是．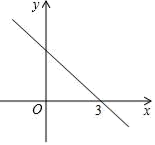

查看试题解析
16. 如图，P是边长为2a的正方形ABCD的对角线BD上的一点，点E是AB的中点，则PA＋PE的最小值是.

查看试题解析

三、解答题

17. 计算

(1)、 $\sqrt{12} + \sqrt{\frac{1}{3}} - \sqrt{27}$

(2)、 ${(1 - \sqrt{2})}^{2} + \sqrt{16} \div \sqrt{2}$

查看试题解析
18. 如图，在平面直角坐标系 $x O y$ 中，一次函数 $y = k x + b$ 的图象经过点 $A (- 2 ， 4)$ ，且与正比例函数 $y = - \frac{2}{3} x$ 的图象交于点 $B (a ， 2)$ .

(1)、求a的值及一次函数 $y = k x + b$ 的解析式；

(2)、直接写出关于x的不等式 $- \frac{2}{3} x > k x + b$ 的解集.

查看试题解析
19. 如图， $E ， F$ 是正方形 $A B C D$ 的对角线 $A C$ 上的两点， $A E = C F$ .证明：四边形 $B E D F$ 是菱形.

查看试题解析
20. 如图，在 $7 \times 5$ 的方格纸 $A B C D$ 中，请按要求画图，且所画格点三角形的顶点分别落在格点四边形 $A B C D$ 的不同边上，且不与点A，B，C，D重合.

(1)、在图1中画一个 $△ E F G$ ，使得 $E F ： F G = 3 ： 4$ .

(2)、在图2中画一个等腰 $△ M N P$ ，使得 $M N ⊥ N P$ .

查看试题解析
21. 一个正方体物体沿斜坡向下滑动，其截面如图所示.正方形DEFH的边长为2米，坡角∠A＝30°，∠B＝90°，BC＝6米.当正方形DEFH运动到什么位置，即当AE为多少米时，有 $D C^{2} = A E^{2} + B C^{2}$ .（提示：连接DC）.

查看试题解析

22. 随着寒冬的来临，“新冠”疫情再次肆虑，育才中学为让学生了解“新冠病毒”传染情况，增强学生的防护意识，开展了“远离新冠·珍受生命”的防“新冠”安全知识测试活动，现从学校八、九年级中各随机抽取15名学生的测试成绩（满分10分，8分及8分以上为优秀）进行整理、描述和分析，下面给出了部分信息：

八年级15名学生的测试成绩是：8，7，9，9，5，9，9，8，9，9，5，8，8，9，8

八，九年级抽取的学生的测试成绩的平均数、众数、中位数、8分及以上人数所占百分比如下表所示：

年级	平均数	众数	中位数	8分及以上人数所占百分比
八年级	8	a	8	$80 %$
九年级	8	9	b	c

九年级15名学生的测试成绩条形统计图如图：

根据以上信息，解答下列问题：

(1)、直接写出上述表中的a，b，c的值：

(2)、根据以上数据，你认为该校八、九年级中哪个年级学生掌握防“新冠”安全知识更好？请说明理由（一条即可）：

(3)、育才中学八年级、九年级各1600名学生参加了此次测试活动，估计参加此次测试活动获得成绩优秀

(x \geq 8)

的学生人数是多少？

查看试题解析

23. 如图，在 $△ A B C$ 中， $A D$ 是 $B C$ 边上的中线，E是 $A D$ 的中点，过点A作 $A F / / B C$ 交 $B E$ 的延长线于点F，连结 $C F$ .

(1)、求证： $△ B D E ≌ △ F A E$ .

(2)、当 $A B = A C$ 时，求证：四边形 $A D C F$ 是矩形.

查看试题解析
24. 在抗击疫情期间，某社区准备购买酒精和消毒液两种消毒物资供居民使用．第一次购买酒精20瓶，消毒液20瓶，共花费300元；第二次购买酒精15瓶，消毒液40瓶，共花费350元．

(1)、分别求出每瓶酒精和消毒液的价格；

(2)、若要购买60瓶这两种消毒物资，设购买酒精x瓶，这两种消毒物资的总费用为y元，求y与x的函数解析式；

(3)、在（2）的条件下，若要求购买酒精的数量不少于消毒液数量的2倍，求总费用y的最小值．

查看试题解析
25. 在平面直角坐标系中，点O为坐标原点，点A、B、C的坐标分别是（6，0）、（6，8）、（0，8），∠OBC的平分线交y轴、x轴分别交于点D、F，且DE⊥OB于E.

(1)、则线段OE的长为；

(2)、求点D的坐标；

(3)、若点M在直线 $2 y + x = 0$ 上，当△ODM是等腰三角形时，求出点M的坐标.

查看试题解析

成绩	70	89	96	100
人数	1	2	3	1

分数（分）	91	92	93	94	95
评委（位）	1	2	1	2	1