浙教版科学九年级上第三章 杠杆专题拔尖训练（０.２）
试卷更新日期：2021-08-08 类型：同步测试
一、单选题
-
1. 如图甲所示的力学装置，杠杆OAB始终在水平位置保持平衡，O为杠杆的支点，OB=20A，竖直细杆a的上端通过力传感器相连在天花板上，下端连接杠杆的A点，竖直细杆b的两端分别与杠杆的B点和物体M固定，水箱的质量为0.8kg，底面积为200cm2 ， 不计杠杆、细杆及连接处的重力，力传感器可以显示出细杆a的上端受到作用力的大小，图乙是力传感器的示数大小随水箱中水的质量变化的图像，则（ ）
A、物体M的密度为0.6×103kg/m3 B、当传感器示数为0N时，加水质量为1.4kg C、当加水质量为1.8kg时，容器对桌面的压强为 D、加水质量为2kg时，水对水箱底部的压力为31N2. 在杠杆的两端挂着质量和体积都相同的铝球和铁球，这时杠杆平衡；将两球分别浸泡在质量和溶质质量分数都相同的稀硫酸中(如图所示)，直至两个烧杯中均没有气泡产生为止，两球的外形变化不大且无孔洞出现。下列推测中正确的是（ ）
①反应结束后，烧杯甲中的溶液质量大； ②反应结束后，烧杯乙中的溶液质量大；
③拿掉烧杯后，要使杠杆重新平衡，支点应向A 端移动；
④拿掉烧杯后，要使杠杆重新平衡，支点应向B 端移动
A、①③ B、①④ C、②③ D、②④3. 如图，小明用一轻质杠杆自制简易密度秤的过程中，在A端的空桶内分别注入密度已知的不同液体，改变物体M悬挂点B的位置，当杠杆在水平位置平衡时，在M悬挂点处标出相应液体的密度值，下列关于密度秤制作的说法中，正确的是（ ）
A、悬点O适当左移，秤的量程会增大 B、秤的刻度值分布不均匀 C、增大M的质量，秤的量程会减小 D、每次倒入空桶的液体质量相同4. 如图所示，光滑带槽的长木条AB（质量不计）可以绕支点O转动，木条的A端用竖直细线连接在地板上，OA=0.6m，OB=0.4m。在木条的B端通过细线悬挂一个长方体木块C，C的密度为0.8×103kg/m3 ， B端正下方放一盛满水的溢水杯。现将木块C缓慢浸入溢水杯中，当木块浸入水中一半时，从溢水口处溢出0.5N的水，杠杆处于水平平衡状态，然后让质量为300g的小球从B点沿槽向A端匀速运动，经4s的时间系在A端细绳的拉力恰好等于0，下列结果不正确的是（忽略细线的重力，g取10N/kg）（ ）
A、木块受到的浮力为0.5N B、木块C受到细线的拉力为0.3N C、小球刚放在B端时A端受到细线的拉力为2.2N D、小球的运动速度为0.2m/s5. 如图所示，一根木棒 AB 在 O 点被悬挂起来，AO=OC，在 A、C 两点分别挂有两个和三个相同的钩码，木棒处于平衡状态。如在木棒的 A、C 点各增加一个同样的钩码，则木棒 （ ）
A、绕 O 点顺时针方向转动 B、绕O 点逆时针方向转动 C、平衡可能被破坏，转动方向不定 D、仍能保持平衡状态6. 一根金属棒AB置于水平地面上，现通过弹簧测力计竖直地将棒的右端B缓慢拉起，如图甲所示。在此过程中，弹簧测力计对棒所做的功W与B端离开地面的高度x的关系如图乙所示。根据图像，下列说法中正确的是（ ）
A、该金属棒的长度L＝1.6m B、在B端拉起的过程中，当x1＝0.6m时，测力计的示数为F1＝1.5N C、当x2＝1.6m时，测力计的示数为F2＝5N D、金属棒的重心到A端的距离为0.6m7. 现有一根形变不计、长为L的铁条AB和两根横截面积相同、长度分别为La、Lb的铝条a、b。将铝条a叠在铁条AB上，并使它们的右端对齐，然后把它们放置在三角形支架O上，AB水平平衡，此时OB的距离恰好为La ， 如图所示。取下铝条a后，将铝条b按上述操作方法使铁条AB再次水平平衡，此时OB的距离为Lx。下列判断正确的是（ ）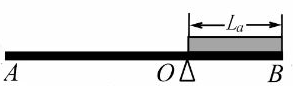
A、若La<Lb<L，则La<Lx< 成立 B、若La<Lb<L，则Lx > 成立 C、若Lb <La ， 则 < Lx<La成立 D、若Lb <La ， 则Lx < 成立8. 如图所示，AOB为一杠杆(质量忽略不计) ， 物体悬挂在A端并浸没在水中，B端在F力作用下竖直向下拉。在烧杯中不断加入蔗糖固体搅拌溶解(溶解过程中溶液温度和体积不变)，若杠杆仍水平平衡，拉力F与溶解的蔗糖质量关系如下图，其中表示正确的是（ ）
A、
B、
C、
D、
9. 如图所示甲乙两杠杆处于水平位置平衡，甲图上有两个体积不同的铁球，乙图上有两个体积相同的铝球和铁球，如果把他们都浸没在水中，则杠杆将发生的变化是（ ）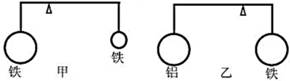
A、仍保持平衡 B、都失去平衡 C、甲仍保持平衡，乙失去平衡 D、甲失去平衡，乙仍保持平衡10. 如图，一质量分布均匀的12kg 铁球与轻杆 AB焊接于 A点后悬挂于竖直墙壁的 B点，轻杆的延长线过球心O，轻杆的长度是铁球半径的 2/3。要使铁球刚好离开墙壁，施加在铁球上的力至少为（ ）
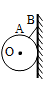A、27N B、45N C、72N D、90N11. 材料相同的甲、乙两个物体分别挂在杠杆A、B两端，O为支点（OA<OB），如图所示，杠杆处于平衡状态．如果将甲、乙物体（不溶于水）浸没于水中，杠杆将会（ ）
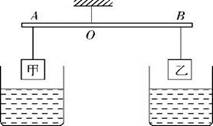A、A端下沉 B、B端下沉 C、仍保持平衡 D、无法确定12. 如图是上肢力量健身器示意图。杠杆AB可绕O点在竖直平面内转动，AB=3BO，配重的重力为120牛。重力为500牛的健身者通过细绳在B点施加竖直向下的拉力为F1时，杠杆在水平位置平衡，配重对地面的压力为85牛。在B点施加竖直向下的拉力为F2时，杠杆仍在水平位置平衡，配重对地面的压力为60牛。已知F1：F2=2：3，杠杆AB和细绳的质量及所有摩擦均忽略不计。下列说法正确的是（ ）
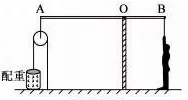A、配重对地面的压力为50牛时，健身者在B点施加竖直向下的拉力为160牛 B、配重对地面的压力为90牛时，健身者在B点施加竖直向下的拉力为120牛 C、健身者在B点施加400牛竖直向下的拉力时，配重对地面的压力为35牛 D、配重刚好被匀速拉起时，健身者在B点施加竖直向下的拉力为540牛13. 如图所示，AB是一质量为m的均匀细直杆，A端靠在光滑的竖直墙壁上，B端置于水平地面上，杆身与竖直方向夹角为θ为30°，杆保持平衡，则此时地面对细杆的支持力与摩擦力分别为（ ）
A、mg mg B、mg mg C、 mg mg D、2mg mg14. 一块厚度、密度均匀长方形水泥板平放在水平地面上，现分别用竖直向上的力F甲和F乙作用在不同的位置(如图甲、乙)，将其一端缓缓抬离地面，则下列说法正确的是（ ）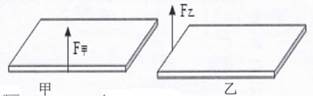
A、F甲>F乙 ， 因为甲图中的动力臂长 B、F甲<F乙 ， 因为乙图中的阻力臂长 C、F甲>F乙 ， 因为乙图中时阻力臂短 D、F甲=F乙 ， 因为两图中动力臂都是阻力臂的2倍15. 育英学校高中部扩建，需要在新旧校址间建立一座桥梁。工人王师傅借助河中石头，要把竹竿尽可能深地插入湖底淤泥，如图所示，效果最好的是（ ）A、
B、
C、
D、
16. 如图，在探究杠杆平衡条件时，左边的钩码个数和位置保持不变，右边弹簧测力计的作用点固定，只改变测力计与水平方向的角θ，则能描述测力计示数 Fθ关系的图象是（ ）A、
B、
C、
D、
17. 如图，小明用一轻质杠杆自制简易密度秤的过程中，在A端的空桶内分别注入密度已知的不同液体，改变物体M悬挂点B的位置，当杠杆在水平位置平衡时，在M悬挂点处标出相应液体的密度值。下列关于密度秤制作的说法中，错误的是（ ）
A、每次倒入空桶的液体体积相同 B、秤的刻度值向右越来越大 C、悬点O适当右移，秤的量程会增大 D、增大M的质量，秤的量程会增大18. 如图，OAB是杠杆，OA与BA垂直，在OA的中点挂一个10N的重物，加在B点的动力使OA在水平位置保持静止（杠杆重力及摩擦均不计），则（ ）
A、该杠杆一定是省力杠杆 B、作用点在B点的最小动力小于5N C、该杠杆一定是费力杠杆 D、作用点在B点的最小动力等于5N19. 杠杆OA的B点挂着重物G ， A端用细绳挂在圆弧EF上，此时OA恰成水平，且A点与圆弧形架EF的圆心重合。当绳AM的M端从E点缓慢滑到F点的过程中，绳对A点拉力的大小将（ ）
A、逐渐变大 B、逐渐变小 C、先变大再变小 D、先变小再变大20. 如图所示，密度分布均匀的圆柱形棒的一端悬挂一个小铁块并一起浸入水中。平衡时棒浮出水面的长度是浸入水中长度的n倍。若水的密度为ρ，则棒的密度为（ ）
A、 B、 C、 D、二、填空题
-
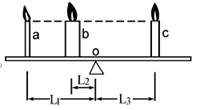
21. 如图所示，一均匀木条可绕转轴O自由转动，现有材料相同，长度相同，横截面积之比Sa：Sb：Sc=1：4：2的三支蜡烛a、b、c，垂直立于木条上，木条恰好处于平衡。三支蜡烛离转轴的距离分别为L1、L2和L3 ， 若L1=4L2 ， 则L3=L2。若同时点燃蜡烛蜡烛在燃烧过程中，要使杠杆保持平衡，则L1：L2：L3=(蜡烛在相等时间内燃烧的质量相同)。
22. 古代护城河上有座吊桥，它的结构原理如图所示。把桥面看成是长为10m，所受重力为3000N的均匀杆OA ， 可以绕转轴O点在竖直平面内转动，在O点正上方10m处固定一个定滑轮，绳子通过定滑轮与杆的另一端A相连，用力拉动绳子就可以将杆从水平位置缓慢向上拉起。杆即将离开水平位置时，绳子的拉力为F1 ， 当士兵们把吊桥拉起到与水平面的夹角为30°时，绳子的拉力为F2 ， 所用的时间是0.5min(忽略绳子重力、滑轮半径和摩擦)。则：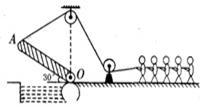
(1)、F1：F2=。(2)、士兵们对吊桥做功的平均功率是W。23. 建筑工人利用如图所示的两种方式，将重为 600N 的材料运送到 3 m 高的楼顶上，图甲中 A 端用绳子悬挂材料，B 端拉力 F1始终沿竖直方向，OB = 2OA，在此过程中拉力 F1将（选填“变大”、“变小”或“不变”）；图乙中斜面长 6 m、高 3 m，沿斜面方向施加400N 的拉力 F2匀速将材料也成功运送到楼顶，物体所受斜面的摩擦力为N。
24. 如图所示，一轻质杠杆支在支架上，OA=20cm，G1为边长是5cm的正方体，G2重为20N。当OC=10cm时，绳子的拉力为N，此时G1对地面的压强为2×104Pa。现用一水平拉力，使G2以cm/s的速度向右匀速运动，经过12.5s后，可使G1对地面的压力恰好为零。
25. 如图所示，在处于水平位置平衡的杠杆的A点悬挂两个总重为2N的钩码，在B点用弹簧测力计竖直向上拉，使杠杆在水平位置再次平衡，则拉力应为N，此时的杠杆属于(选填“省力”或“费力”)杠杆。如果弹簧测力计的量程为0～5N，在支点不变的情况下，采用图中的杠杆，能较为精确地测量出悬挂物体的最大质量为kg。(g取10N/kg)
26. 如图所示，质量为m的人站在质量为 的均匀木板AB中点，木板可以绕B端转动，要使木板处于水平状态不动，此人拉力的大小为。(摩擦忽略不计)
三、解答题
-
27. 如图甲，有一轻质杆，左右各挂由同种金属制成，质量分别为m1和m2(m1>m2)的实心物块后恰好水平平衡
(1)、求左右悬挂点到支点O的距离L1与L2之比
(2)、将两物分别浸没在水中，杆将会 ▲ （选填“左端下降”“右端下降”“仍然平衡”），试通过推导说明。28. 为探究平衡木受力的特点，重为400N的小科设计了图甲所示的平衡木模型，整个装置放在水平地面上，AB可绕支点O无摩擦转动。AB始终处于水平平衡状态，C处固定一竖直硬杆，硬杆重300N，硬杆的底部安装有压力传感器R，R所在的电路装置如图乙所示，R的阻值随着硬杆对它的压力F的变化关系如图丙所示。其中，电源电压为4.5V，保护电阻R0=5Ω，电流表的量程为0～0.6A，且AB=4m，OA=BC=1m，整个装置除硬杆外，其他部分的重力均不计，求：
(1)、小科的质量为kg；(2)、小科站在A点时，C处受到硬杆对它的拉力；(3)、小科站在C点时，电流表的示数；(4)、在电路安全的情况下，小科在平衡木上缓慢走动的过程中，当电路消耗的电功率达到最小值和最大值时，压力传感器R消耗的电功率之比。29. 一根质量分布不均匀，长度为1.2米、重为9N的金属棒AB置于水平地面上，用弹簧测力计始终竖直方向拉棒的B端使其缓慢匀速拉起离开地面，如图甲所示。
(1)、在此过程中，弹簧测力计对棒所做的功W与B端离开地面的高度h的关系，如图乙所示，其中最合理的是。(2)、在B端拉起的过程中，当h1=1m时，测力计的示数F1为3N；由此推断：金属棒的重心到A的距离d=；(3)、拉B端使金属棒缓慢匀速拉起，当h2=2m时，求这个过程中拉力做了多少功？30. 质量为 2.5kg 的圆柱体，其横截面的半径为 0.5m；放置在水平地面上，与高为 0.2m的台阶接触，接触部位足够粗糙，如图所示。现欲在圆柱体上施加一作用力，使它下部刚好脱离地面。(1)、画出此作用力F最小的示意图(2)、求此作用力F的最小值。(3)、要使此圆柱体在10s内运动到台阶上，则功率至少为多少？31. 如图甲所示，正方体A边长0.2m，作为配重使用，杠杆OE：OF=2：3，某同学用这个装置和一个密闭容器D提取水中的圆柱体B， 圆柱体B的体积是密闭容器D的1/3；旁边浮体C的体积是0.1m3 ， 该同学站在浮体C上，总体积的3/5浸入水中；该同学用力拉动滑轮组绕绳自由端，手拉绳的功率P和密闭容器D匀速被提升的距离关系如图乙所示；密闭容器D上升速度0.05m/s保持不变，密闭容器D被提出水后，圆柱体B从密闭容器D中取出放在浮体C的上面，同时手松开绳子时，浮体C露出水面的体积减少总体积的7/25；在提升全过程中，配重A始终没有离开地面。两个定滑轮总重10 N.（绳的重力，滑轮与轴的摩擦及水的阻力不计。g＝10N/kg），求：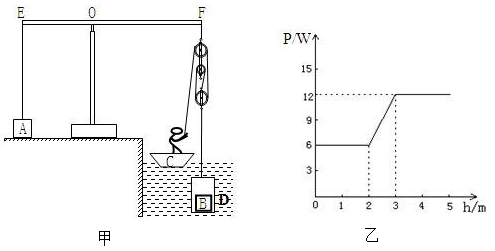
(1)、圆柱体B的重力；(2)、密闭容器D离开水面时，滑轮组提升重物B的机械效率；（百分号前面保留一位小数）；(3)、圆柱体B的密度；(4)、在提升全过程中配重A对地面的压强的最大变化量。四、实验探究题
-
32. 下列是某科学研究小组探究杠杆平衡条件的实验过程：(本实验均使用轻质杠杆)实验1：在直杠杆水平平衡时(如图甲所示) 进行实验， 记录多组数据。得出：F1×s1=F2× s2(注：s1和s2分别表示支点到F1和F2的作用点的距离)。在直杠杆倾斜平衡时(如图乙所示)进行实验，也得到了同样的结论。该结论适用于所有平衡时的杠杆吗?
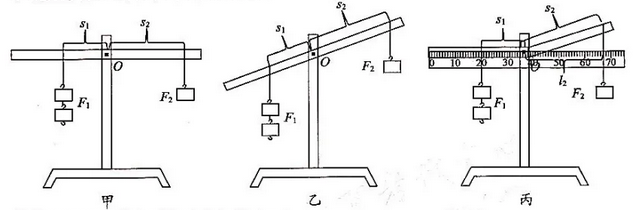
实验2：科学研究小组用一侧弯曲的杠杆进行如图丙所示的实验，移动钩码，改变钩码数量，
记录数据如表，分析表格数据发现上述结论并不成立，但发现一个新的等量关系，即：(待填)。s和l(支点到力的作用线的距离)这两个量在研究杠杆平衡条件时，哪个量才是有价值的呢?研究小组的同学观察到：支点到F的作用点的距离(s1)与支点到F1的作用线的距离(l1)是相等的。研究小组的同学又进行了实验。
实验3：
实验次数
F1/N
S1/cm
F2/N
S2/cm
L2/cm
1
1.0
10.0
0.5
21.3
20.1
2
1.5
20.0
1.0
31.7
29.8
3
2.0
30.0
2.5
25.5
24.0
①移动钩码，使杠杆________，并使杠杆处于平衡状态。
②记录F1、s1、l1和F2、s2、l2。
③改变钩码数量，移动钩码，记录杠杆处于平衡时的多组F1、s1、l1和F2、s2、l2。
④分析实验数据，得出弯杠杆的平衡条件。最后，通过科学思维，得出所有杠杆的平衡条件都是：F1×l1=F2×l2。杠杆的平衡条件可用于解释许多杠杆应用，如用图1方式提升物体比用图2方式省力，就可用杠杆的平衡条件作出合理解释。请回答：
(1)、在研究一侧弯曲的杠杆时，发现的一个新的等量关系是。(2)、将实验3中的①填写完整。(3)、“支点到力的作用线的距离”在科学上被称为。通过探究杠杆平衡条件的实验，使我们深深认识到建立这一科学量的价值。(4)、用图1方式提升物体比用图2方式省力的原因是。33. 同学们利用实验共同验证“杠杆的平衡条件”．实验中使用的杠杆刻线均匀，每个钩码的质量都相等．
(1)、杠杆初始状态如图甲所示，为使杠杆处于水平平衡状态，此时应将杠杆的平衡螺母均向调节．(2)、杠杆调节完毕后，莉莉在杠杆支点两侧挂的钩码如图乙所示，如果此时莉莉不再支撑杠杆，杠杆不能静止在水平位置．同学们给出了自己的判断和建议：①小红说，把右侧的钩码减掉一个，杠杆就平衡了．
②小林说，把左侧的钩码向左移动一格，杠杆就平衡了．
③小健说，在左侧的钩码下增加一个钩码，杠杆就平衡了．
④小东说，在右侧的钩码下增加一个钩码，并向左移动一格，杠杆也可以平衡．你认为都有谁说对了（填序号）．
(3)、乙图中钩码均重0.5N，体积均为4立方厘米，在盛有某液体的烧杯置于右侧钩码下方，当最下端的一个钩码浸没于该液体中时，杠杆在水平位置静止，该液体密度为kg/m3。34. 教室内的日光灯一般都是由两条竖直平行的吊链吊在天花板上的(如图甲所示)，两条吊链竖直平行除了美观外，还蕴含着科学道理。
(1)、图甲中a、b是挂日光灯的吊链。若以吊链a的固定点O作为支点，F甲作为拉力时，可将灯视作(选填“省力”“费力”或“等臂”)杠杆。(2)、比较图甲、图乙两种悬挂方式，图甲吊链受到的拉力大小为F甲 ， 图乙吊链受到的拉力大小为F乙 ， 则F甲F乙(选填“＞”“＝”或“＜”)。(3)、若图甲中b吊链突然断开后日光灯将绕O点转动，此时日光灯的重力势能将(选填“增大”“减小”或“不变”)。35. 某同学要测一个金属块的密度，他手中的测量工具只有一只量程较小的弹簧测力计，当他用此弹簧测力计测量该金属块的重力时，发现已超过弹簧测力计的最大量程，于是他设计了如图所示的装置去测量。图中OA：OB=1：3。他实验的步骤如下：
⑴用细绳把金属块悬挂于A点，用弹簧测力计在B点作用一个竖直向上的力，使杠杆OAB在水平位置静止，金属块静止在空中，读出弹簧测力计此时的读数F1；
⑵向容器中加适量的水，“适量”指的是 ， 待杆在水平位置重新平衡后，再读出弹簧测力计此时的读数F2 ， 则F1F2（选填“大于”、“等于”、“小于”）；
⑶若杠杆OAB质量不计，则被测金属块密度的表达式：ρ=。（水的密度表示为ρ水）
36. 小江用如图所示的实验装置测量杠杆的机械效率，实验时竖直向上拉动杠杆，使挂在杠杆下面的钩码缓缓上升。（支点和杠杆的摩擦不计）问：
(1)、重为5N的钩码挂在为点时，人的拉力F为4N。钩码上升0.3m时，动力作用点C上升0.5 m，此时机械效率η1为。(2)、小江为了进一步研究杠杆的机械效率与哪些因素有关，仍用该实验装置，将钩码移到更靠近支点的B点处，再次缓慢提升杠杆，使动力作用点C仍然上升0.5 m。问：人的拉力F与第一次相比（选填“变大”、“变小”或“不变”），此时的机械效率η2与第一次相比会（选填“变大”、“变小”或“不变”）。37. 在“探究杠杆平衡条件”实验中，小科用一块T形板对实验装置进行改进。如图甲所示，T形板上有槽口ab和卡口cd，T形板通过槽口ab可以绕着杠杆的0点自由旋转并上下移动，弹簧测力计与一根质量可以忽略的碳素细棒MN相连，碳素细棒MN刚好卡入T形板的卡口cd，如图乙所示。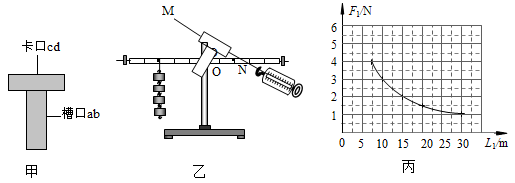
(1)、小想认为要完成这个实验，还需要一把刻度尺，但小科认为只要在T形板上稍微进行改进，不添加器材也可完成实验。小科对T形板进行的改进方法是 。(2)、利用这个装置进行实验的优点为：。(3)、小科在实验过程中，保持阻力、阻力臂不变，在杠杆水平平衡时，测出每一组动力臂L1和动力F1的数据，并利用实验数据绘制了F1与L1的关系图像，如图丙所示。请根据图像推算，当L1为5cm时，F1为N。