贵州省遵义市2021年中考数学试卷
试卷更新日期:2021-08-06 类型:中考真卷
一、单选题
-
1. 在下列四个实数中,最小的实数是( )A、 B、0 C、3.14 D、20212. 下列美术字中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、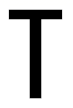 D、
D、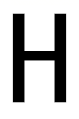 3. 如图,已知直线a//b,c为截线,若∠1=60°,则∠2的度数是( )
3. 如图,已知直线a//b,c为截线,若∠1=60°,则∠2的度数是( )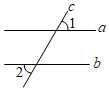 A、30° B、60° C、120° D、150°4. 下列计算正确的是( )A、a3•a=a3 B、(a2)3=a5 C、4a•(﹣3ab)=﹣12a2b D、(﹣3a2)3=﹣9a65. 小明用30元购买铅笔和签字笔,已知铅笔和签字笔的单价分别是2元和5元,他买了2支铅笔后,最多还能买几支签字笔?设小明还能买x支签字笔,则下列不等关系正确的是( )A、5×2+2x≥30 B、5×2+2x≤30 C、2×2+2x≥30 D、2×2+5x≤306. 已知反比例函数y (k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
A、30° B、60° C、120° D、150°4. 下列计算正确的是( )A、a3•a=a3 B、(a2)3=a5 C、4a•(﹣3ab)=﹣12a2b D、(﹣3a2)3=﹣9a65. 小明用30元购买铅笔和签字笔,已知铅笔和签字笔的单价分别是2元和5元,他买了2支铅笔后,最多还能买几支签字笔?设小明还能买x支签字笔,则下列不等关系正确的是( )A、5×2+2x≥30 B、5×2+2x≤30 C、2×2+2x≥30 D、2×2+5x≤306. 已知反比例函数y (k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )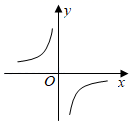 A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限7. 如图,▱ABCD的对角线AC,BD相交于点O,则下列结论一定正确的是( )
A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限7. 如图,▱ABCD的对角线AC,BD相交于点O,则下列结论一定正确的是( )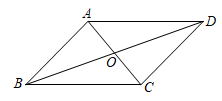 A、OB=OD B、AB=BC C、AC⊥BD D、∠ABD=∠CBD8. 数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如a+bi(a,b为实数)的数叫做复数,用z=a+bi表示,任何一个复数z=a+bi在平面直角坐标系中都可以用有序数对Z(a,b)表示,如:z=1+2i表示为Z(1,2),则z=2﹣i可表示为( )A、Z(2,0) B、Z(2,﹣1) C、Z(2,1) D、Z(﹣1,2)9. 在解一元二次方程x2+px+q=0时,小红看错了常数项q,得到方程的两个根是﹣3,1.小明看错了一次项系数P,得到方程的两个根是5,﹣4,则原来的方程是( )A、x2+2x﹣3=0 B、x2+2x﹣20=0 C、x2﹣2x﹣20=0 D、x2﹣2x﹣3=010. 如图,将矩形纸片ABCD的两个直角进行折叠,使CB,AD恰好落在对角线AC上,B′,D′分别是B,D的对应点,折痕分别为CF,AE.若AB=4,BC=3,则线段 的长是( )
A、OB=OD B、AB=BC C、AC⊥BD D、∠ABD=∠CBD8. 数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如a+bi(a,b为实数)的数叫做复数,用z=a+bi表示,任何一个复数z=a+bi在平面直角坐标系中都可以用有序数对Z(a,b)表示,如:z=1+2i表示为Z(1,2),则z=2﹣i可表示为( )A、Z(2,0) B、Z(2,﹣1) C、Z(2,1) D、Z(﹣1,2)9. 在解一元二次方程x2+px+q=0时,小红看错了常数项q,得到方程的两个根是﹣3,1.小明看错了一次项系数P,得到方程的两个根是5,﹣4,则原来的方程是( )A、x2+2x﹣3=0 B、x2+2x﹣20=0 C、x2﹣2x﹣20=0 D、x2﹣2x﹣3=010. 如图,将矩形纸片ABCD的两个直角进行折叠,使CB,AD恰好落在对角线AC上,B′,D′分别是B,D的对应点,折痕分别为CF,AE.若AB=4,BC=3,则线段 的长是( ) A、 B、2 C、 D、111. 如图,点C是以点O为圆心,AB为直径的半圆上一点,连接AC,BC,OC.若AC=4,BC=3,则sin∠BOC的值是( )
A、 B、2 C、 D、111. 如图,点C是以点O为圆心,AB为直径的半圆上一点,连接AC,BC,OC.若AC=4,BC=3,则sin∠BOC的值是( )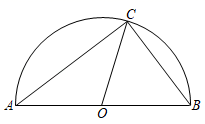 A、1 B、 C、 D、12. 如图,AB是⊙O的弦,等边三角形OCD的边CD与⊙O相切于点P,连接OA,OB,OP,AD.若∠COD+∠AOB=180°, AB=6,则AD的长是( )
A、1 B、 C、 D、12. 如图,AB是⊙O的弦,等边三角形OCD的边CD与⊙O相切于点P,连接OA,OB,OP,AD.若∠COD+∠AOB=180°, AB=6,则AD的长是( )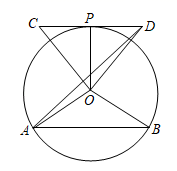 A、6 B、3 C、2 D、
A、6 B、3 C、2 D、二、填空题
-
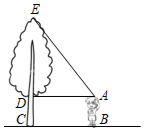
13. 2021年5月15日,中国火星探测器“天问一号“在火星表面成功着陆,着陆点距离地球约为320000000千米,将数320000000用科学记数法表示为 .14. 已知x,y满足的方程组是 ,则x+y的值为 .15. 小明用一块含有60°(∠DAE=60°)的直角三角尺测量校园内某棵树的高度,示意图如图所示,若小明的眼睛与地面之间的垂直高度AB为1.62m,小明与树之间的水平距离BC为4m,则这棵树的高度约为 m.(结果精确到0.1m,参考数据: 1.73)
 16. 抛物线y=ax2+bx+c(a,b,c为常数,a>0)经过(0,0),(4,0)两点.则下列四个结论正确的有 (填写序号).
16. 抛物线y=ax2+bx+c(a,b,c为常数,a>0)经过(0,0),(4,0)两点.则下列四个结论正确的有 (填写序号).①4a+b=0;
②5a+3b+2c>0;
③若该抛物线y=ax2+bx+c与直线y=﹣3有交点,则a的取值范围是a ;
④对于a的每一个确定值,如果一元二次方程ax2+bx+c﹣t=0(t为常数,t≤0)的根为整数,则t的值只有3个.
三、解答题
-
17.(1)、计算(﹣1)2+| 2| 2sin45°;(2)、解不等式组: .18. 先化简 ( ),再求值,其中x 2.19. 《国家学生体质健康标准》规定:九年级学生50m测试成绩分为优秀、良好、及格,不及格四个等级,某中学为了了解九年级学生的体质健康状况,对九年级学生进行50m测试,并随机抽取50名男生的成绩进行分析,将成绩分等级制作成不完整的统计表和条形统计图,根据图表信息,解答下列问题:
等级
人数
优秀
4
良好
a
及格
28
不及格
b
合计
50
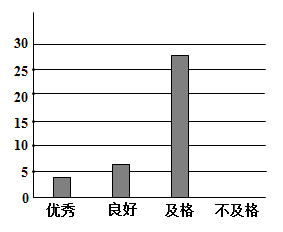 (1)、统计表中a的值是 ;(2)、将条形统计图补充完整;(3)、将等级为优秀、良好、及格定为达标,求这50名男生的达标率;(4)、全校九年共有350名男生,估计不及格的男生大约有多少人?20. 现有A,B两个不透明的袋子,A袋的4个小球分别标有数字1,2,3,4;B袋的3个小球分别标有数字1,2,3.(每个袋中的小球除数字外,其它完全相同.)(1)、从A,B两个袋中各随机摸出一个小球,则两个小球上数字相同的概率是 ;(2)、甲、乙两人玩摸球游戏,规则是:甲从A袋中随机摸出一个小球,乙从B袋中随机摸出一个小球,若甲、乙两人摸到小球的数字之和为奇数时,则甲胜;否则乙胜,用列表或树状图的方法说明这个规则对甲、乙两人是否公平.21. 在复习菱形的判定方法时,某同学进行了画图探究,其作法和图形如下:
(1)、统计表中a的值是 ;(2)、将条形统计图补充完整;(3)、将等级为优秀、良好、及格定为达标,求这50名男生的达标率;(4)、全校九年共有350名男生,估计不及格的男生大约有多少人?20. 现有A,B两个不透明的袋子,A袋的4个小球分别标有数字1,2,3,4;B袋的3个小球分别标有数字1,2,3.(每个袋中的小球除数字外,其它完全相同.)(1)、从A,B两个袋中各随机摸出一个小球,则两个小球上数字相同的概率是 ;(2)、甲、乙两人玩摸球游戏,规则是:甲从A袋中随机摸出一个小球,乙从B袋中随机摸出一个小球,若甲、乙两人摸到小球的数字之和为奇数时,则甲胜;否则乙胜,用列表或树状图的方法说明这个规则对甲、乙两人是否公平.21. 在复习菱形的判定方法时,某同学进行了画图探究,其作法和图形如下:①画线段AB;
②分别以点A,B为圆心,大于AB长的一半为半径作弧,两弧相交于M、N两点,作直线MN交AB于点O;
③在直线MN上取一点C(不与点O重合),连接AC、BC;
④过点A作平行于BC的直线AD,交直线MN于点D,连接BD.
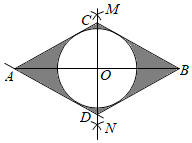 (1)、根据以上作法,证明四边形ADBC是菱形;(2)、该同学在图形上继续探究,他以点O为圆心作四边形ADBC的内切圆,构成如图所示的阴影部分,若AB=2 ,∠BAD=30°,求图中阴影部分的面积.22. 为增加农民收入,助力乡村振兴.某驻村干部指导农户进行草莓种植和销售,已知草莓的种植成本为8元/千克,经市场调查发现,今年五一期间草莓的销售量y(千克)与销售单价x(元/千克)(8≤x≤40)满足的函数图象如图所示.
(1)、根据以上作法,证明四边形ADBC是菱形;(2)、该同学在图形上继续探究,他以点O为圆心作四边形ADBC的内切圆,构成如图所示的阴影部分,若AB=2 ,∠BAD=30°,求图中阴影部分的面积.22. 为增加农民收入,助力乡村振兴.某驻村干部指导农户进行草莓种植和销售,已知草莓的种植成本为8元/千克,经市场调查发现,今年五一期间草莓的销售量y(千克)与销售单价x(元/千克)(8≤x≤40)满足的函数图象如图所示.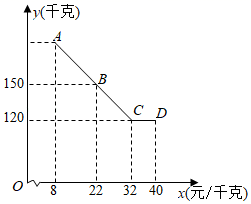 (1)、根据图象信息,求y与x的函数关系式;(2)、求五一期间销售草莓获得的最大利润.23. 如图,抛物线y=a(x﹣2)2+3(a为常数且a≠0)与y轴交于点A(0, ).
(1)、根据图象信息,求y与x的函数关系式;(2)、求五一期间销售草莓获得的最大利润.23. 如图,抛物线y=a(x﹣2)2+3(a为常数且a≠0)与y轴交于点A(0, ).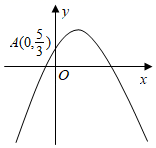 (1)、求该抛物线的解析式;(2)、若直线y=kx (k≠0)与抛物线有两个交点,交点的横坐标分别为x1 , x2 , 当x12+x22=10时,求k的值;(3)、当﹣4<x≤m时,y有最大值 ,求m的值.24. 点A是半径为2 的⊙O上一动点,点B是⊙O外一定点,OB=6.连接OA,AB.
(1)、求该抛物线的解析式;(2)、若直线y=kx (k≠0)与抛物线有两个交点,交点的横坐标分别为x1 , x2 , 当x12+x22=10时,求k的值;(3)、当﹣4<x≤m时,y有最大值 ,求m的值.24. 点A是半径为2 的⊙O上一动点,点B是⊙O外一定点,OB=6.连接OA,AB.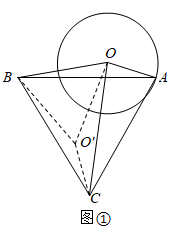

 (1)、(阅读感知)如图①,当△ABC是等边三角形时,连接OC,求OC的最大值;将下列解答过程补充完整.
(1)、(阅读感知)如图①,当△ABC是等边三角形时,连接OC,求OC的最大值;将下列解答过程补充完整.解:将线段OB绕点B顺时针旋转60°到O′B,连接OO′,CO′.
由旋转的性质知:∠OBO′=60°,BO′=BO=6,即△OBO′是等边三角形.
∴OO′=BO=6
又∵△ABC是等边三角形
∴∠ABC=60°,AB=BC
∴∠OBO′=∠ABC=60°
∴∠OBA=∠O′BC
在△OBA和△O′BC中,
∴(SAS)
∴OA=O′C
在△OO′C中,OC<OO′+O′C
当O,O′,C三点共线,且点C在OO′的延长线上时,OC=OO′+O′C
即OC≤OO′+O′C
∴当O,O′,C三点共线,且点C在OO′的延长线上时,OC取最大值,最大值是 .
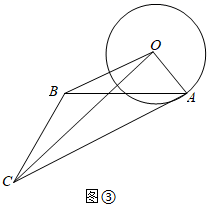
(2)、(类比探究)如图②,当四边形ABCD是正方形时,连接OC,求OC的最小值;(3)、(理解运用)如图③,当△ABC是以AB为腰,顶角为120°的等腰三角形时,连接OC,求OC的最小值,并直接写出此时△ABC的周长.