广西百色市2021年中考数学试卷
试卷更新日期:2021-08-06 类型:中考真卷
一、单选题
-
1. ﹣2022的相反数是( )A、﹣2022 B、2022 C、±2022 D、20212. 如图,与∠1是内错角的是( )
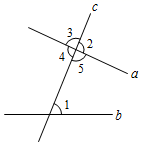 A、∠2 B、∠3 C、∠4 D、∠53. 骰子各面上的点数分别是1,2,…,6,抛掷一枚骰子,点数是偶数的概率是( )A、 B、 C、 D、14. 已知∠α=25°30′,则它的余角为( )A、25°30′ B、64°30′ C、74°30′ D、154°30′5. 方程 = 的解是( ).A、x=﹣2 B、x=﹣1 C、x=1 D、x=36. 一组数据4,6,x,7,10的众数是7,则这组数据的平均数是( )A、5 B、6.4 C、6.8 D、77. 下列各式计算正确的是( )A、33=9 B、(a﹣b)2=a2﹣b2 C、2 +3 =5 D、(2a2b)3=8a8b38. 下列展开图中,不是正方体展开图的是( )A、
A、∠2 B、∠3 C、∠4 D、∠53. 骰子各面上的点数分别是1,2,…,6,抛掷一枚骰子,点数是偶数的概率是( )A、 B、 C、 D、14. 已知∠α=25°30′,则它的余角为( )A、25°30′ B、64°30′ C、74°30′ D、154°30′5. 方程 = 的解是( ).A、x=﹣2 B、x=﹣1 C、x=1 D、x=36. 一组数据4,6,x,7,10的众数是7,则这组数据的平均数是( )A、5 B、6.4 C、6.8 D、77. 下列各式计算正确的是( )A、33=9 B、(a﹣b)2=a2﹣b2 C、2 +3 =5 D、(2a2b)3=8a8b38. 下列展开图中,不是正方体展开图的是( )A、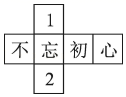 B、
B、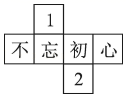 C、
C、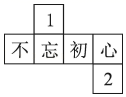 D、
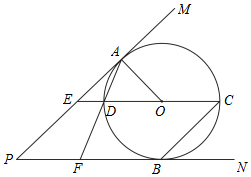
D、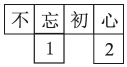 9. 如图,在⊙O中,尺规作图的部分作法如下:(1)分别以弦AB的端点A、B为圆心,适当等长为半径画弧,使两弧相交于点M;(2)作直线OM交AB于点N.若OB=10,AB=16,则tan∠B等于( )
9. 如图,在⊙O中,尺规作图的部分作法如下:(1)分别以弦AB的端点A、B为圆心,适当等长为半径画弧,使两弧相交于点M;(2)作直线OM交AB于点N.若OB=10,AB=16,则tan∠B等于( )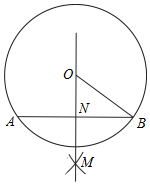 A、 B、 C、 D、10. 当x=﹣2时,分式 的值是( )A、﹣15 B、﹣3 C、3 D、1511. 下列四个命题:①直径是圆的对称轴;②若两个相似四边形的相似比是1:3,则它们的周长比是1:3,面积比是1:6;③同一平面内垂直于同一直线的两条直线互相平行;④对角线相等且互相垂直的平行四边形是正方形.其中真命题有( )A、①③ B、①④ C、③④ D、②③④12. 如图,矩形ABCD各边中点分别是E、F、G、H,AB=2 ,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是( )
A、 B、 C、 D、10. 当x=﹣2时,分式 的值是( )A、﹣15 B、﹣3 C、3 D、1511. 下列四个命题:①直径是圆的对称轴;②若两个相似四边形的相似比是1:3,则它们的周长比是1:3,面积比是1:6;③同一平面内垂直于同一直线的两条直线互相平行;④对角线相等且互相垂直的平行四边形是正方形.其中真命题有( )A、①③ B、①④ C、③④ D、②③④12. 如图,矩形ABCD各边中点分别是E、F、G、H,AB=2 ,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 的倒数是.14. 某公司开展“爱心公益”活动,将价值16000元的物品捐赠给山区小学,数据16000用科学记数法表示为.15. 如图,是一组数据的折线统计图,则这组数据的中位数是.
 16. 实数 的整数部分是.17. 数学活动小组为测量山顶电视塔的高度,在塔的椭圆平台遥控无人机.当无人机飞到点P处时,与平台中心O点的水平距离为15米,测得塔顶A点的仰角为30°,塔底B点的俯角为60°,则电视塔的高度为米.
16. 实数 的整数部分是.17. 数学活动小组为测量山顶电视塔的高度,在塔的椭圆平台遥控无人机.当无人机飞到点P处时,与平台中心O点的水平距离为15米,测得塔顶A点的仰角为30°,塔底B点的俯角为60°,则电视塔的高度为米.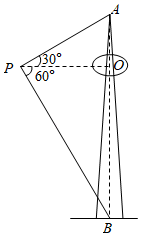 18. 如图,△ABC中,AB=AC,∠B=72°,∠ACB的平分线CD交AB于点D,则点D是线段AB的黄金分割点.若AC=2,则BD=.
18. 如图,△ABC中,AB=AC,∠B=72°,∠ACB的平分线CD交AB于点D,则点D是线段AB的黄金分割点.若AC=2,则BD=.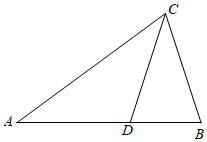
三、解答题
-
19. 计算:(π﹣1)0+| ﹣2|﹣( )﹣1+tan60°.20. 解不等式组 ,并把解集在数轴上表示出来.21. 如图,O为坐标原点,直线l⊥y轴,垂足为M,反比例函数y= (k≠0)的图象与l交于点A(m,3),△AOM的面积为6
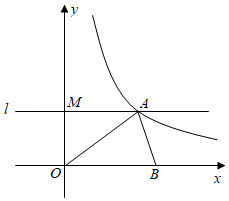 (1)、求m、k的值;(2)、在x轴正半轴上取一点B,使OB=OA,求直线AB的函数表达式.22. 如图,点D、E分别是AB、AC的中点,BE、CD相交于点O,∠B=∠C,BD=CE.求证:
(1)、求m、k的值;(2)、在x轴正半轴上取一点B,使OB=OA,求直线AB的函数表达式.22. 如图,点D、E分别是AB、AC的中点,BE、CD相交于点O,∠B=∠C,BD=CE.求证: (1)、OD=OE;(2)、△ABE≌△ACD.23. 为了解某校九年级500名学生周六做家务的情况,黄老师从中随机抽取了部分学生进行调查,将他们某一周六做家务的时间t(小时)分成四类(A:0≤t<1,B:1≤t<2,C:2≤t<3,D:t≥3),并绘制如下不完整的统计表和扇形统计图.
(1)、OD=OE;(2)、△ABE≌△ACD.23. 为了解某校九年级500名学生周六做家务的情况,黄老师从中随机抽取了部分学生进行调查,将他们某一周六做家务的时间t(小时)分成四类(A:0≤t<1,B:1≤t<2,C:2≤t<3,D:t≥3),并绘制如下不完整的统计表和扇形统计图.类别
A
B
C
D
人数
2
18
3

根据所给信息:
(1)、求被抽查的学生人数;(2)、周六做家务2小时以上(含2小时)为“热爱劳动”,请你估计该校九年级“热爱劳动”的学生人数;(3)、为让更多学生积极做家务,从A类与D类学生中任选2人进行交流,求恰好选中A类与D类各一人的概率(用画树状图或列表法把所有可能结果表示出来).24. 据国际田联《田径场地设施标准手册》,400米标准跑道由两个平行的直道和两个半径相等的弯道组成,有8条跑道,每条跑道宽1.2米,直道长87米;跑道的弯道是半圆形,环形跑道第一圈(最内圈)弯道半径为35.00米到38.00米之间.某校据国际田联标准和学校场地实际,建成第一圈弯道半径为36米的标准跑道.小王同学计算了各圈的长:
第一圈长:87×2+2π(36+1.2×0)≈400(米);
第二圈长:87×2+2π(36+1.2×1)≈408(米);
第三圈长:87×2+2π(36+1.2×2)≈415(米);
……
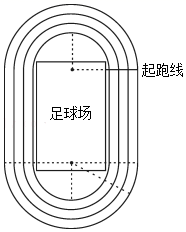
请问:
(1)、第三圈半圆形弯道长比第一圈半圆形弯道长多多少米?小王计算的第八圈长是多少?(2)、小王紧靠第一圈边线逆时针跑步、邓教练紧靠第三圈边线顺时针骑自行车(均以所靠边线长计路程),在如图的起跑线同时出发,经过20秒两人在直道第一次相遇.若邓教练平均速度是小王平均速度的2倍,求他们的平均速度各是多少?(注:在同侧直道,过两人所在点的直线与跑道边线垂直时,称两人直道相遇)