四川省成都市青羊区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-06 类型：期末考试

进入出卷网下载

一、单选题

1. 若分式 $\frac{6 x}{x - 5}$ 有意义，则x满足的条件是（）

A、 $x = 5$ B、 $x \neq 5$ C、 $x = 0$ D、 $x \neq 0$

查看试题解析
2. 下面的图形既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若m＞n，则下列不等式一定成立的是（）

A、m＋1＜n＋1 B、m﹣2＜n﹣2 C、3m＞3n D、﹣4m＞4n

查看试题解析
4. 如果一个多边形的内角和等于720°，则它的边数为（）

A、3 B、4 C、5 D、6

查看试题解析
5. 在平面直角坐标系中，将点A（5，3）向左平移3个单位，得到的点的坐标是（）

A、（8，3） B、（5，6） C、（5，0） D、（2，3）

查看试题解析
6. 已知两个不等式的解集在数轴上如右图表示，那么这个解集为（）

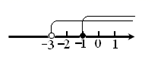A、x≥－1 B、 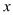>1 C、－3<x≤－1 D、x>－3

查看试题解析
7. 如图，射线a、b分别与直线l交于点A、B，现将射线a沿直线l向右平移过点B，若∠1＝44°，∠2＝66°，则∠3的度数为（）

A、66° B、68° C、70° D、72°

查看试题解析
8. 在下列平行四边形性质的叙述中，错误的是（）

A、平行四边形的对边相等 B、平行四边形的对角相等 C、平行四边形的对角线互相平分 D、平行四边形的对角线相等

查看试题解析
9. 如图，在△ABE中，∠E＝25°，AE的垂直平分线MN交BE于点C，连接AC，若AB＝AC，那么∠BAE的度数是（）

A、100° B、105° C、110° D、120°

查看试题解析
10. 如图，已知▱ABCD的顶点C（4，0），D（7，4），点B在x轴负半轴上，点A在y轴正半轴上，以顶点C为圆心，适当长为半径画弧，分别交CB、CD于点E、F，再分别以点E、F为圆心，大于 $\frac{1}{2}$ EF的长为半径画弧，两弧交于点G，作射线CG交边AD于点M.则点M的坐标为（）

A、（1，4） B、（2，4） C、（3，4） D、（1.5，4）

查看试题解析

二、填空题

11. 因式分解： $n^{2} - 4$ ＝.

查看试题解析
12. 若 $\sqrt{a - 3}$ ＋|b＋2|＝0，则分式 $\frac{a + b}{a - b}$ 的值是.

查看试题解析
13. 如图，直线l₁：y＝x＋3与直线l₂：y＝kx＋b在同一平面直角坐标系中相交于一点，则关于x的不等式x＋3＜kx＋b的解集是.

查看试题解析
14. 如图，在Rt△ACB中，∠ACB＝90°，BC＝6，AC＝9.折叠△ACB，使点A与BC的中点D重合，折痕交AB于E，交AC于点F，则CF＝.

查看试题解析
15. 若m﹣2n＝3，则m²﹣4mn＋4n²﹣10＝.

查看试题解析
16. 若分式方程 $\frac{x}{x - 2}$ ＝2＋ $\frac{a}{x - 2}$ 的解为正数，则a的取值范围是.

查看试题解析
17. 从0，1，2，3，4这5个数中任选一个数作为m的值，则使不等方式组 ${\begin{matrix} x < 2 \\ x > m \end{matrix}$ 无实数解，且使得正比例函数y＝（m﹣4）x中因变量y随自变量x的增大而减小的概率是.

查看试题解析
18. 如图，△ABC与△CDE都是等边三角形，连接AD、BE.CD＝2，BC＝1，若将△CDE绕点C顺时针旋转，当点A、C、E在同一条直线上时，线段BE的长为.

查看试题解析
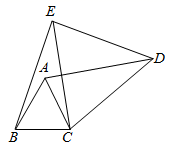19. 如图，△ABC中，∠B＝45°，∠C＝75°，AB＝4，D为BC上一动点，过D作DE⊥AC于点E，作DF⊥AB于点F，连接EF，则EF的最小值为.

查看试题解析

三、解答题

20. 计算下列各题

(1)、解不等式组： ${\begin{matrix} 3 (x + 2) > x - 2 \\ 3 - \frac{2}{3} \leq \frac{1 + x}{2} \end{matrix}$ ；

(2)、解方程： $\frac{1}{x - 2}$ ＝ $\frac{1 - x}{2 - x}$ ﹣3

查看试题解析
21. 先化简，再求值：（1﹣ $\frac{3}{x + 2}$ ）÷ $\frac{x^{2} - 2 x + 1}{5 x + 10}$ ，其中x＝ $\sqrt{5}$ ＋1

查看试题解析
22. 如图，在平面直角坐标系中，已知A（﹣2，4），B（﹣4，1），C（﹣1，2）.

（ 1 ）画出△ABC绕点O逆时针旋转90°后的图形△A₁B₁C₁；

（ 2 ）将△ABC先向右平移5个单位再向下平移2个单位得到△△A₂B₂C₂ ，画出△A₂B₂C₂

查看试题解析
23. 如图，▱ABCD的对角线AC与BD相交于点O，过点B作BE⊥AC于点E，过点D作DF⊥AC于点F，连接DE、BF.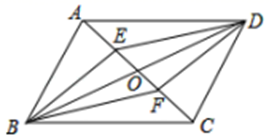

(1)、求证：四边形BEDF为平行四边形；

(2)、若BE＝8，EF＝6，求BD的长.

查看试题解析
24. 2021年6月15日凌晨3时许，成都至自贡高速铁路立交双线特大桥成功实现合龙，为成自高铁如期建成开通奠定坚实的基础.其中某一段工程招标时，工程指挥部收到甲、乙两个工程队的投标书，根据甲、乙两队的投标书测算：若让甲队单独完成这项工程需要40天；若由乙队先做10天，剩下的工程由甲、乙两队合作20天才可完成.那么安排乙队单独完成这项工程需要多少天？

查看试题解析
25. 如图，已知△ABC是等边三角形，AB＝8，M为AC中点，D为BC边上一动点，将AD绕点A逆时针旋转60°得到AE，连接CE、DE、ME.

(1)、求证：CD＋CE＝CA；

(2)、求出点M到CE所在直线的距离；

(3)、当ME＝ $\frac{7}{2}$ 时，求CE的值.

查看试题解析
26. 三星堆遗址最新出土的“黄金大面具”来自于5号坑，由四川省文物考古研究院与四川大学考古文博学院联合发掘为保护文物，特别设计了A、B两种型号的运土车.已知2辆A型运土车与3辆B型运土车一次共运输土方31立方米，5辆A型运土车与6辆B型运土车一次共运输土方70立方米.

(1)、一辆A型运土车和一辆B型运土车一次各运输土方多少？

(2)、考古专家组决定派出A、B两种型号运土车共20辆参与运输土方，若每次运输土方总量不小于148立方米，且B型运土车至少派出2辆，则有哪几种派车方案？

查看试题解析
27. 在平面直角坐标系中，直线l₁：y＝2x＋3与过点B（6，0）的直线l₂交于点C（1，m），与x轴交于点A，与y轴交于点E，直线l₂与y轴交于点D.

(1)、求直线的函数解析式；

(2)、如图1，点F在直线l₂位于第二象限的图象上，使得 $S_{△ B E F} = 4 \cdot S_{△ O E F}$ ，求点F的坐标.

(3)、如图2，在线段BC存在点M，使得△CEM是以CM为腰的等腰三角形，求M点坐标.

查看试题解析
28. 在△ABC中，∠ACB＝90°，AC＝BC，点D为AB的中点，点E是AC上一点.连接DE，过D作DF⊥DE交BC点于F，连接EF.

(1)、如图1，EF与CD相交于点G：
①来证：AE＝CF；

②当AD＝CE，AC＝6时，求DG；

(2)、如图2，点M为BC上一点，且∠CME＝2∠ADE，AE＝2，CE＝5，求EM的长.

查看试题解析