四川省成都市郫都区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下列防疫标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、（a²）³＝a⁵ B、a⁶÷a²＝a³ C、（ab）³＝a³b³ D、a³•a²＝a⁶

查看试题解析
3. 如图所示，工人师傅在砌门时，通常用木条BD固定长方形门框ABCD ，使其不变形这样做的数学根据是（）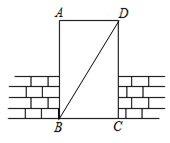

A、三角形具有稳定性 B、两点之间，线段最短 C、对顶角相等 D、垂线段最短

查看试题解析
4. 下列语句所描述的事件中，是不可能事件的是（）

A、黄河入海流 B、大漠孤烟直 C、手可摘星辰 D、红豆生南国

查看试题解析
5. 正方形的边长为4，若边长增加x，那么面积增加y，则y关于x的函数表达式为（）

A、 $y = x^{2} + 16$ B、 $y = {(x + 4)}^{2}$ C、 $y = x^{2} + 8 x$ D、 $y = 16 - 4 x^{2}$

查看试题解析
6. 掷一枚质地均匀硬币，前3次都是正面朝上，掷第4次时正面朝上的概率是（）

A、0 B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
7. 如图所示，不能推出a∥b的条件是（）

A、∠4＝∠2 B、∠1＝∠3 C、∠1+∠2＝180° D、∠1+∠4＝180°

查看试题解析
8. 如图，在△ABC中，∠B＝30°，用直尺和圆规在边AB上确定一点D ，则∠ADC＝（）

A、30° B、45° C、50° D、60°

查看试题解析
9. 将长为12的线段截成长度为整数的三段，使它们成为一个三角形的三边，则构成的三角形不可能是（）

A、等腰三角形 B、钝角三角形 C、等边三角形 D、直角三角形

查看试题解析

二、填空题

10. 计算：（ $\frac{2020}{2021}$ ﹣π）⁰＝．

查看试题解析
11. 如图，OP平分∠AOB ， PC⊥OA ，点D是OB上的动点，若PC＝1cm，则PD的长的最小值为．

查看试题解析
12. 声音在空气中传播的速度 $y (m / s)$ （简称声速）与气温 $x$ （℃）的关系如下表所示：

气温 $x$ /℃

0

5

10

15

20

…

声速 $y / (m / s)$

331

334

337

340

343

…

照此规律可以发现，当气温 $x$ 为℃时，声速 $y$ 达到 $352 m / s$ ．

查看试题解析
13. 已知：1纳米＝1×10^﹣9米．用科学记数法表示：250纳米＝米．

查看试题解析
14. 如图，一个圆形转盘被分成6个圆心角都是60°的扇形．任意转动这个转盘1次，当转动停止时，指针指向阴影区域的概率为．

查看试题解析
15. 一个人驱车前进时，两次拐弯后，按原来的相反方向前进，若第一次拐弯是向右转85°，则第二次拐弯是向右转的度数为．

查看试题解析
16. 如图所示，A村、B村都在河边CD的同侧，已知AC＝1km，BD＝3km，CD＝3km．若在河边CD上选点建水厂，则A村、B村到水厂的距离之和的最小值为．

查看试题解析
17. 如图，四边形ABCD是正方形，AE⊥BE于点E ，且AB＝13k ， AE＝5k ，设阴影部分的面积为S ，则S与k的数量关系为．

查看试题解析

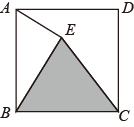
三、解答题

18.

(1)、计算：3a（2a﹣4）+（a+3）（4a﹣5）；

(2)、先化简，再求值：[（x﹣2y）²﹣（x+y）（x﹣y）﹣3y²]÷（﹣2y），其中x＝﹣2，y＝﹣3．

查看试题解析
19. 下列正方形网格图中，部分方格涂上了阴影，请按照不同要求作图．

(1)、如图①，整个图形是轴对称图形，画出它的对称轴；

(2)、如图②，将某一个方格涂上阴影，使整个图形有两条对称轴；

(3)、如图③，将某一个方格涂上阴影，使整个图形有四条对称轴．

查看试题解析
20. 不透明的口袋里装有红、黄、蓝三种颜色的小球（除颜色外其余都相同），其中红球有2个，蓝球有1个，已知从袋中任意摸出一个是红球的概率为 $\frac{1}{5}$ ．

(1)、从袋中任意摸出一个是蓝球的概率是多少？

(2)、求袋中黄球的个数．

查看试题解析
21. 如图，在四边形ABD中，已知BE平分∠ABC ，交AD于E ，且AB＝AE ．解答下列问题，并要求标注推导理由：

(1)、求证：AD∥BC；

(2)、若AB∥DC ， ∠D＝122°，求∠3的大小．

查看试题解析
22. 如图，在Rt△ABC中，∠ACB＝90°，AD平分∠CAB交BC于点D ，点E在AB上，且AE＝AC ，连接DE ．

(1)、求证：△ADE≌△ADC；

(2)、若E为AB中点，求∠B的度数；

(3)、若AC＝6，BC＝8，求BD的长．

查看试题解析
23. 如图1，四边形ABCD中，AB∥CD ， ∠ADC＝90°，P从A点出发，以每秒1单位长度的速度，按A﹣B﹣C﹣D的顺序在边上匀速运动．如图2，自变量t（秒）表示P点的运动时间，因变量S表示△PAD的面积．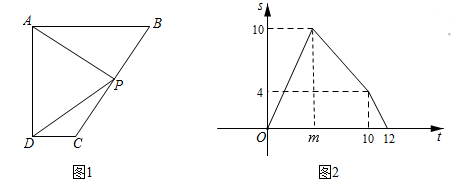

(1)、当点P从点C运动到点D时，用了多少时间？CD的长为多少？AD的长为多少？

(2)、求m的值；

(3)、当P运动到BC中点时，估算S的值．

查看试题解析
24. 如图1是一个长为4a ，宽为b的长方形，沿图中虚线用剪刀分成四个全等的小长方形，然后用这四块小长方形拼成如图2的正方形．

(1)、观察图2，直接写出（a+b）² ，（a﹣b）² ， ab三者的等量关系式；

(2)、①用（1）的结论解答：①若m+2m^﹣1＝3，求m﹣2m^﹣1的值；
②如图3，正方形ABCD与AEFG边长分别为x ， y ．若xy＝15，BE＝2，求图3中阴影部分的面积和．

查看试题解析
25. 如图，△ABC中，∠ABC＝60°，分别以AB ， AC为边向三角形外作等边△ABD和等边△ACE ，解答下列各题，并要求标注推导理由：

(1)、如图1，求证：AD∥BC；

(2)、如图2，连接CD、BE ，求证：DC＝BE；

(3)、如图3，若∠ACB=90°，连接DE ，交AB于点F ，求证：DF＝EF ．

查看试题解析

气温 $x$ /℃	0	5	10	15	20	…
声速 $y / (m / s)$	331	334	337	340	343	…