四川省成都市龙泉驿区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-08-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知 $x > y$ ，则下列不等式成立的是（）

A、 $2 x - 5 > 2 y - 5$ B、 $x + 3 < y + 3$ C、 $5 x < 5 y$ D、 $- 2 x > - 2 y$

查看试题解析
3. 下列各式变形中，是因式分解的是（）

A、 $a^{2} - 2 a b + b^{2} - 1 = {(a - b)}^{2} - 1$ B、 $2 x^{2} + 2 x = 2 x^{2} (1 + \frac{1}{x})$ C、 $(x + 2) (x - 2) = x^{2} - 4$ D、 $x^{2} - 6 x + 9 = {(x - 3)}^{2}$

查看试题解析
4. 多边形每一个外角都是 $45 °$ ，那么这个多边形是（）

A、六边形 B、七边形 C、八边形 D、九边形

查看试题解析
5. 要使式子 $\frac{\sqrt{a + 2}}{a}$ 有意义，a的取值范围是（）

A、a≠0 B、a＞－2 C、a＞－2或a≠0 D、a≥－2且a≠0

查看试题解析
6. 下列各式： $\frac{x}{2}, \frac{x - 1}{x + 2}, \frac{4}{3} x y^{2}, \frac{1}{b}, \frac{3 x y}{π}$ 其中是分式的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图△ABC向下平移n个单位得到△A'B'C’，若点B的坐标为（﹣2，1），则点B的对应点B'的坐标为（）

A、（﹣2，1+n） B、（﹣2，1﹣n） C、（﹣2+n，1） D、（﹣2﹣n，1）

查看试题解析
8. 方程 $\frac{2 - x}{x - 5} - \frac{3}{5 - x}$ ＝0的解为（）

A、﹣2 B、2 C、5 D、无解

查看试题解析
9. 如图，Rt△OAB的斜边OA在y轴上，∠AOB＝30°，OB＝ $\sqrt{3}$ ，将Rt△AOB绕原点顺时针旋转90°，则A的对应点A₁的坐标为（）

A、（1， $\sqrt{3}$ ） B、（﹣1， $\sqrt{3}$ ） C、（2，0） D、（﹣2，0）

查看试题解析
10. 如图，Rt△ABC中，CD⊥AB于D，下列结论中：①∠1＝∠A；②∠2+∠B＝90°；③CD²＝AD•BD；④BC²＝BD•AD，一定成立的有（）个

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 分解因式：x²﹣4= ．

查看试题解析
12. 不等式 $3 ﹣ 2 x > 7$ 的解集为.

查看试题解析
13. 已知 $\frac{a}{b} = \frac{2}{5}$ ，则 $\frac{b - a}{b + a}$ ＝.

查看试题解析
14. 如图，在菱形ABCD中，对角线AC，BD交于点O，其中CA＝2，OB＝3，则菱形ABCD的面积为.

查看试题解析
15. 已知ab＝﹣3，a+b＝2.则 $\frac{1}{a} + \frac{1}{b}$ ＝.

查看试题解析
16. 若关于x的分式方程 $\frac{2}{x - 3} = 1 - \frac{m}{x - 3}$ 有增根，则m=.

查看试题解析
17. 如图，点A、B在数轴上所表示的数分别是x、x＋1，点C在线段AB上（点C不与点A、B重合）.若点C在数轴上表示的数是2x，则x的取值范围是.

查看试题解析
18. 如图，在四边形ABCD中，AD∥BC.BC＝2AD，若S_△AOD＝1，则S_△ABC＝.

查看试题解析
19. 如图，已知正方形ABCD，点E为对角线AC上一点（不与A，C重合），过点E作EF⊥DE交BC于点F.连接DF，则 $\frac{D E}{E F}$ 的值等于.

查看试题解析

三、解答题

20. 计算：

(1)、因式分解： $a^{2} b - 4 a b^{2} + 4 b^{3}$ ；

(2)、解不等式组： ${\begin{array}{l} 5 + 2 (x - 3) ⩽ 3 \\ \frac{3 - x}{2} < x \end{array}$ .

查看试题解析
21. 计算：

(1)、解方程： $\frac{x - 1}{4 - x} = 2 - \frac{6}{x - 4}$ ；

(2)、先化简，再求值： $\frac{x - 1}{x^{2} + 2 x + 1} \div (1 - \frac{2}{x + 1})$ ，其中x＝ $\sqrt{3} - 1$ .

查看试题解析
22. 如图：AD∥EG∥BC，EG分别交AB，DB，AC于点E，F，G，已知AD＝5，BC＝10，AE＝9，AB＝12.求EG，FG的长.

查看试题解析
23. 小刚和小亮想用测量工具和几何知识测量公园古树 $A B$ 的高度，由于有围栏保护，他们无法到达底部 $B$ ，如图，围栏 $C D = 29$ 米，小刚在 $D C$ 延长线 $E$ 点放一平面镜，镜子不动，当小刚走到点 $F$ 时，恰好可以通过镜子看到树顶 $A$ ，这时小刚眼睛 $G$ 与地面的高度 $F G = 1.5$ 米， $E F = 2$ 米， $E C = 1$ 米；同时，小亮在 $C D$ 的延长线上的 $H$ 处安装了测倾器（测倾器的高度忽略不计），测得树顶 $A$ 的仰角 $∠ A H B = 45 °$ ， $D H = 5$ 米，请根据题中提供的相关信息，求出古树 $A B$ 的高度.

查看试题解析
24. 如图，已知正方形DEFG的边EF在△ABC的边BC上，顶点D，G分别在边AB，AC上，AH⊥BC于H.BC＝15，AH＝10.求正方形DEFG的边长和面积.

查看试题解析
25. 如图

(1)、如图1，在四边形ABCD中，点M在BC上，∠B＝∠C＝∠AMD时.求证：△ABM∽△MCD.

(2)、如图2，在△ABC中，点M是边BC的中点，点D，E分别在边AB，AC上.若∠B＝∠C＝∠DME＝45°，BC＝8 $\sqrt{2}$ ，CE＝6，求DE的长.

查看试题解析
26. 如图，矩形OABC中，AO＝4，AB＝8，点E，F分别在边AB，OC上，且AE＝3，将矩形的部分沿直线EF翻折，点A的对应点A'恰好落在对角线AC上，求OF的长.

查看试题解析
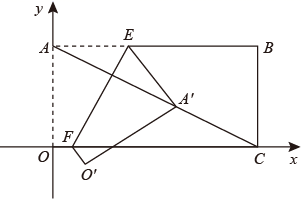27. 如图，正方形ABCD中，AB＝2，E为DC右侧一点，且DE＝DC，（∠CDE＜90°）.连接AE.

(1)、若∠CDE＝20°.求∠DAE的度数；

(2)、过点A作射线EC的垂线段，垂足为P，求证AE＝ $\sqrt{2}$ AP；

(3)、在（2）的条件下，AP与BC交于点F，当BF＝FC时，求CE的长.

查看试题解析
28. 如图

(1)、如图1，Rt△ABC与Rt△ADE，∠ADE＝∠ABC＝90°， $\frac{A B}{B C} = \frac{A D}{D E} = \frac{1}{2}$ ，连接BD，CE.求证： $\frac{B D}{C E} = \frac{\sqrt{5}}{5}$ .

(2)、如图2，四边形ABCD，∠BAD＝∠BCD＝90°，且 $\frac{A B}{A D} = \frac{1}{2}$ ，连接BC，BC、AC、CD之间有何数量关系？
小明在完成本题中，如图3，使用了“旋转放缩”的技巧，即将△ABC绕点A逆时针旋转90°，并放大2倍，点B对应点D.点C落点为点E，连接DE，请你根据以上思路直接写出BC，AC，CD之间的关系.

(3)、拓展：如图4，矩形ABCD，E为线段AD上一点，以CE为边，在其右侧作矩形CEFG，且 $\frac{A B}{B C} = \frac{C E}{E F} = \frac{1}{2}$ ，AB＝5，连接BE，BF.求BE+ $\frac{\sqrt{5}}{5}$ BF的最小值.

查看试题解析