四川省成都市锦江区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-08-06 类型:期末考试
一、单选题
-
1. 许多数学符号蕴含着对称美,在下列数学符号中,既是轴对称图形,又是中心对称图形的符号是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列由左边到右边的变形,属于因式分解的是( )A、 B、 C、 D、3. 下列各数是不等式x-1≥0的解的是( )A、-2 B、-1 C、0 D、14. 一个多边形的内角和等于它的外角和的3倍,则它是( )边形.A、六 B、七 C、八 D、九5. 下列分式变形一定成立的是( )A、 B、 C、 D、6. 如图,在 中, ,作 的垂直平分线,交 于点 ,交 于点 ,若 ,则 的长度是( )
2. 下列由左边到右边的变形,属于因式分解的是( )A、 B、 C、 D、3. 下列各数是不等式x-1≥0的解的是( )A、-2 B、-1 C、0 D、14. 一个多边形的内角和等于它的外角和的3倍,则它是( )边形.A、六 B、七 C、八 D、九5. 下列分式变形一定成立的是( )A、 B、 C、 D、6. 如图,在 中, ,作 的垂直平分线,交 于点 ,交 于点 ,若 ,则 的长度是( ) A、3 B、2 C、 D、7. 已知函数 的图象如图所示,则不等式 的解集是( )
A、3 B、2 C、 D、7. 已知函数 的图象如图所示,则不等式 的解集是( ) A、 B、 C、 D、8. 下列命题是真命题的是( )A、斜边及一锐角分别相等的两个直角三角形全等 B、若 则 C、平行四边形对角线相等 D、一组对边相等,另一组对边平行的四边形是平行四边形9. 如图,在 中,对角线 与 交于点 ,点 为 中点,连接 ,若 平分 则 的度数是( )
A、 B、 C、 D、8. 下列命题是真命题的是( )A、斜边及一锐角分别相等的两个直角三角形全等 B、若 则 C、平行四边形对角线相等 D、一组对边相等,另一组对边平行的四边形是平行四边形9. 如图,在 中,对角线 与 交于点 ,点 为 中点,连接 ,若 平分 则 的度数是( ) A、 B、 C、 D、10. 如图, 为 轴负半轴上一点,过点 作 轴,与直线 交于点 ,将 沿直线 向上平移 个单位长度得到 ,若点 的坐标为 ,则点 的坐标是( )
A、 B、 C、 D、10. 如图, 为 轴负半轴上一点,过点 作 轴,与直线 交于点 ,将 沿直线 向上平移 个单位长度得到 ,若点 的坐标为 ,则点 的坐标是( )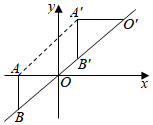 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式: =.12. 若分式 有意义,则 的取值范围是.13. 如图,在 中, ,点 为线段 上一点,连接 将 沿 翻折,点 的对应点 落在 的延长线上,若 则 .
 14. 如图,在 中, 以点 为圆心,适当长为半径画弧,分别交 于点 ,再分别以点 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 射线 与 交于点 ,若 ,则 .
14. 如图,在 中, 以点 为圆心,适当长为半径画弧,分别交 于点 ,再分别以点 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 射线 与 交于点 ,若 ,则 . 15. 已知 则 .16. 如图,直线 与 轴交于点 与 轴交于点 ,直线 与 轴交于点 ,与 轴交于点 ,直线 交于点 ,若 轴上存在点 ,使以 为顶点的四边形是平行四边形,则点 的坐标是.
15. 已知 则 .16. 如图,直线 与 轴交于点 与 轴交于点 ,直线 与 轴交于点 ,与 轴交于点 ,直线 交于点 ,若 轴上存在点 ,使以 为顶点的四边形是平行四边形,则点 的坐标是. 17. 已知不等式组 的解集为 且关于 的方程 的解为正数,则 的取值范围是.18. 如图,在四边形 中, ,四边形 的面积为 ,连接对角线 ,则 的最小值为.
17. 已知不等式组 的解集为 且关于 的方程 的解为正数,则 的取值范围是.18. 如图,在四边形 中, ,四边形 的面积为 ,连接对角线 ,则 的最小值为. 19. 如图,在 中, 为线段 上一点,将 沿 翻折,点 落在点 处,延长 至点 连接 ,且 ,若 ,则 的值是.
19. 如图,在 中, 为线段 上一点,将 沿 翻折,点 落在点 处,延长 至点 连接 ,且 ,若 ,则 的值是.
三、解答题
-
20.(1)、分解因式: .(2)、解方程:21. 解不等式组: 并在数轴上表示出它的解集.
 22. 先化简,再求值: ,其中 .23. 如图,每个小方格的边长为1个单位长度, 的顶点都在格点上,且 的坐标是 的坐标是 .
22. 先化简,再求值: ,其中 .23. 如图,每个小方格的边长为1个单位长度, 的顶点都在格点上,且 的坐标是 的坐标是 .
( 1 )在图中画出平面直角坐标系 ;
( 2 )画出 关于原点 的对称图形 ,并写出点 的坐标;
( 3 )画出 绕点 按顺时针方向旋转 后的图形 ,并写出点 的坐标.
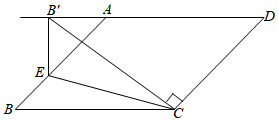
24. 如图,在四边形 中, 延长 至点 使 ,连接 交 于 且 . (1)、求证:四边形 是平行四边形;(2)、若 ,求证: ;(3)、在(2)的条件下,若 求 的面积.25. 如图, 为 的对角线, 平分 为射线 上一点.
(1)、求证:四边形 是平行四边形;(2)、若 ,求证: ;(3)、在(2)的条件下,若 求 的面积.25. 如图, 为 的对角线, 平分 为射线 上一点. (1)、如图1, 在 延长线上,连接 与 交于点 若 ;
(1)、如图1, 在 延长线上,连接 与 交于点 若 ;①当 为 中点时,求证: ;
②当 时,求 长度;
(2)、如图2, 在线段 上,连接 与 交点于 ,若 ,试探究 三条线段之间的数量关系,并说明理由.26. 劳动教育是国民教育体系的重要内容,具有树德、增智、强体、育美等综合育人价值,某校密切联合家庭开展劳动教育课程.暑假期间,部分家长组织学生到户外开展劳动实践活动,一名学生带一名家长,家长联系了甲乙两家组织机构,他们的报价相同,每位学生的报价比家长少20元,按报价计算,家长的总费用为50000元,学生的总费用为48000元.(1)、求家长和学生报价分别是多少元?(2)、经协商,甲机构的优惠条件是:家长全价,学生都按七折收费﹔乙机构的优惠条件是家长、学生都按 为整数)折收费,他们选择了总费用较少的乙机构,请问 的最大值为多少?27. 如图,在 中, 为 中点, 为射线 上一动点,在 右侧作等边 直线 与直线 交于点 . (1)、如图1,当点 与点 重合时,求证: ;(2)、如图2,当点 在线段 上(不包括端点 ), 是否仍然成立,请说明理由;(3)、点 在射线 运动过程中,当 为等腰三角形时,请直接写出 的度数.28. 如图,一次函数 与坐标轴交于 两点,将线段 以点 为中心逆时针旋转一定角度,点 的对应点落在第二象限的点 处,且 的面积为 .
(1)、如图1,当点 与点 重合时,求证: ;(2)、如图2,当点 在线段 上(不包括端点 ), 是否仍然成立,请说明理由;(3)、点 在射线 运动过程中,当 为等腰三角形时,请直接写出 的度数.28. 如图,一次函数 与坐标轴交于 两点,将线段 以点 为中心逆时针旋转一定角度,点 的对应点落在第二象限的点 处,且 的面积为 . (1)、求点 的坐标及直线 的表达式;(2)、点 在直线 上第二象限内一点,在 中有一个内角是 ,求点 的坐标;(3)、过原点 的直线,与直线 交于点 ,与直线 交于点 ,在 三点中,当其中一点是另外两点所连线段的中点时,求 的面积.
(1)、求点 的坐标及直线 的表达式;(2)、点 在直线 上第二象限内一点,在 中有一个内角是 ,求点 的坐标;(3)、过原点 的直线,与直线 交于点 ,与直线 交于点 ,在 三点中,当其中一点是另外两点所连线段的中点时,求 的面积.