四川省成都市金牛区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-08-06 类型:期末考试
一、单选题
-
1. 如果分式 有意义,那么 的取值范围是( )A、 B、 C、 D、2. 地铁是城市生活中的重要交通工具,地铁标志作为城市地铁的形象和符号,出现在城市的每个角落,它是城市文化的缩影.下列城市地铁的标志图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列各式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、4. 六边形的外角和为( )A、180° B、360° C、540° D、720°5. 在平面直角坐标系内,把点 向左平移3个单位,再向上平移2个单位,得到的点 的坐标为( )A、 B、 C、 D、6. 把分式 中的分子分母的 同时扩大为原来的2倍,那么分式的值将( )A、扩大为原来的2倍 B、扩大为原来的4倍 C、不变 D、变为原来的7. 平行四边形 中, 则 的度数为( )A、 B、 C、 D、8. 如图,在 中, 平分 交 于 ,垂足为 .若 则点 到 的距离为( )
3. 下列各式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、4. 六边形的外角和为( )A、180° B、360° C、540° D、720°5. 在平面直角坐标系内,把点 向左平移3个单位,再向上平移2个单位,得到的点 的坐标为( )A、 B、 C、 D、6. 把分式 中的分子分母的 同时扩大为原来的2倍,那么分式的值将( )A、扩大为原来的2倍 B、扩大为原来的4倍 C、不变 D、变为原来的7. 平行四边形 中, 则 的度数为( )A、 B、 C、 D、8. 如图,在 中, 平分 交 于 ,垂足为 .若 则点 到 的距离为( ) A、 B、 C、2 D、9. 菱形 的对角线 ,则菱形 的面积是( )A、80 B、60 C、40 D、3010. 现有 两工厂每小时一共能做900个零件,两个工厂工作相同的时间后,得到 工厂做的96个零件, 工厂做的84个零件,设 工厂每小时能做 个零件,根据题意列出分式方程正确的是( )A、 B、 C、 D、
A、 B、 C、2 D、9. 菱形 的对角线 ,则菱形 的面积是( )A、80 B、60 C、40 D、3010. 现有 两工厂每小时一共能做900个零件,两个工厂工作相同的时间后,得到 工厂做的96个零件, 工厂做的84个零件,设 工厂每小时能做 个零件,根据题意列出分式方程正确的是( )A、 B、 C、 D、二、填空题
-
11. 把 因式分解的结果是.12. 当分式 的值为 时, 的值为.13. 关于 的分式方程 有增根,则 的值是.14. 如图,在 中, 以点 为圆心,以任意长为半径作弧,分别交 于点 ,再分别以 为圆心,以大于 的长为半径作弧,两弧在 内交于点 ,连接 并延长交 于点 若 则 的周长为.
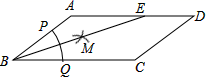 15. 已知 ,则 .16. 在平面直角坐标系 中,一次函数 和 的图象如图所示,则关于 的一元一次不等式 的解集是.
15. 已知 ,则 .16. 在平面直角坐标系 中,一次函数 和 的图象如图所示,则关于 的一元一次不等式 的解集是.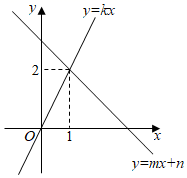 17. 已知 为整数,关于 的方程 有整数解,关于 的不等式组 至少有 个整数解,则符合条件的 值有.18. 如图,长方形 中, 点 是线段 上一动点,连接 ,则 的最小值为.
17. 已知 为整数,关于 的方程 有整数解,关于 的不等式组 至少有 个整数解,则符合条件的 值有.18. 如图,长方形 中, 点 是线段 上一动点,连接 ,则 的最小值为.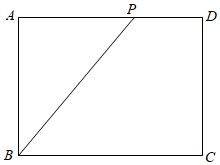 19. 如图,在 中, 延长 到点 ,延长 到点 ,使得 连接 ,延长 交 于点 若 ,则 .
19. 如图,在 中, 延长 到点 ,延长 到点 ,使得 连接 ,延长 交 于点 若 ,则 .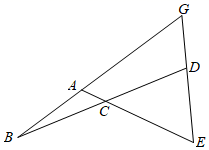
三、解答题
-
20.(1)、解不等式组:(2)、解方程:21. 先化简,再求值: ,其中22. 如图,在平面直角坐标系中,每个小方格都是边长为 个单位的正方形, 的顶点均在格点上,点 的坐标为 .
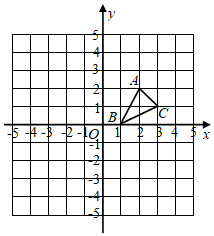
( 1 )画出 向左平移 个单位所得的 ;
( 2 )画出将 绕点 按顺时针旋转 所得的 (点 分别对应点 );
( 3 )线段 的长度为▲ .
23. 四边形 是平行四边形,对角线 交于点 ,点 是 边上一点, 连接 ,求证: .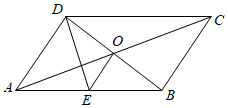 24. 某商场用 元购买甲品牌 恤短袖,用25000元购买乙品牌 恤短袖,购买的乙品牌 恤短袖数量是甲品牌 恤短袖数量的2倍,两种品牌 恤短袖每件进价与利润如下表所示:
24. 某商场用 元购买甲品牌 恤短袖,用25000元购买乙品牌 恤短袖,购买的乙品牌 恤短袖数量是甲品牌 恤短袖数量的2倍,两种品牌 恤短袖每件进价与利润如下表所示:恤短袖品牌
进价(单位:元/件)
利润( 单位:元/件)
甲
8
乙
8
(1)、求 的值.(2)、甲品牌 恤短袖全部降价销售,乙品牌 恤短袖售价不变,上述购买的两种 恤短袖全部售完,利润不低于5500元,则每件甲品牌 恤短袖的降价不超过多少元?25. 如图1,在等边三角形 中, 于 于 与 相交于点 . (1)、求证: ;(2)、如图2,若点 是线段 上一点, 平分 交 所在直线于点 .求证: .(3)、如图3,若点 是线段 上一点(不与点 重合),连接 ,在 下方作 边 交 所在直线于点 .猜想: 三条线段之间的数量关系,并证明.26. 《成都市生活垃圾管理条例》将于2021年3月1日起正式施行,将垃圾按照可回收垃圾、厨余垃圾、有害垃圾和其他垃圾四类进行分类管理某区环卫局准备购买甲、乙两种型号的垃圾箱.经过市场调研发现:购买2个甲型垃圾箱和1个乙型垃圾箱共需320元;购买1个甲型垃圾箱和3个乙型垃圾箱共需460元(1)、求每个甲型垃圾箱和乙型垃圾箱分别为多少元?(2)、该区需要购买甲、乙两种型号的垃圾箱共30个,其中购买甲型垃圾箱不超过20个,且总费用不得超过3300元,请问共有几种购买方案?27. 四边形 和四边形 都是矩形, 与 交于点 与 交于点 .
(1)、求证: ;(2)、如图2,若点 是线段 上一点, 平分 交 所在直线于点 .求证: .(3)、如图3,若点 是线段 上一点(不与点 重合),连接 ,在 下方作 边 交 所在直线于点 .猜想: 三条线段之间的数量关系,并证明.26. 《成都市生活垃圾管理条例》将于2021年3月1日起正式施行,将垃圾按照可回收垃圾、厨余垃圾、有害垃圾和其他垃圾四类进行分类管理某区环卫局准备购买甲、乙两种型号的垃圾箱.经过市场调研发现:购买2个甲型垃圾箱和1个乙型垃圾箱共需320元;购买1个甲型垃圾箱和3个乙型垃圾箱共需460元(1)、求每个甲型垃圾箱和乙型垃圾箱分别为多少元?(2)、该区需要购买甲、乙两种型号的垃圾箱共30个,其中购买甲型垃圾箱不超过20个,且总费用不得超过3300元,请问共有几种购买方案?27. 四边形 和四边形 都是矩形, 与 交于点 与 交于点 . (1)、如图1,当 时,求证: ;(2)、如图2,当 时,连结 ,若 ,求 的值;(3)、如图3,当 时,连结 若 为等边三角形,求 的值28. 如图1,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 与直线 交于点 ,直线 与 轴交于点 .
(1)、如图1,当 时,求证: ;(2)、如图2,当 时,连结 ,若 ,求 的值;(3)、如图3,当 时,连结 若 为等边三角形,求 的值28. 如图1,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 与直线 交于点 ,直线 与 轴交于点 . (1)、求直线 的解析式;(2)、如图2,点 在线段 上,连接 ,过点 的直线交 轴负半轴于点 交 轴正半轴于点 ,请问: 是否为定值?若是,求出定值;若不是,请说明理由.(3)、 当点 在直线 上运动时,平面内是否存在一点 ,使得以点 为顶点的四边形是菱形?若存在,求出点 的坐标;若不存在,请说明理由.
(1)、求直线 的解析式;(2)、如图2,点 在线段 上,连接 ,过点 的直线交 轴负半轴于点 交 轴正半轴于点 ,请问: 是否为定值?若是,求出定值;若不是,请说明理由.(3)、 当点 在直线 上运动时,平面内是否存在一点 ,使得以点 为顶点的四边形是菱形?若存在,求出点 的坐标;若不存在,请说明理由.