重庆市九龙坡区2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2021-08-06 类型:期末考试
一、单选题
-
1. 下列实数中,最小的是( )A、0 B、 C、 D、2. 在下列所示的四个汽车标志图案中,其中可以看作由“基本图案”经过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在平面直角坐标系中,点(3,—4)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列调查方式,你认为最合适的是( )A、了解杨家坪步行街每天的流动人口数,采用抽样调查方式 B、旅客上飞机前的安检,采用抽样调查方式 C、了解重庆市居民端午小长假期间的出行方式,采用全面调查方式 D、日光灯管厂要检测一批灯管的使用寿命,采用全面调查方式5. 若 是关于 的二元一次方程 的解,则a的值是( )A、1 B、2 C、3 D、46. 不等式 的最大整数解为 ( )A、2 B、3 C、4 D、57. 估计 的值在下列哪两个整数之间( )A、6和7之间 B、7和8之间 C、8和9之间 D、9和10之间8. 《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术.其中方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有共买鸡,人出八,盈三;人出七,不足四问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,多余3钱,每人出7钱,还缺4钱.问人数和鸡的价钱各是多少?”设人数有 人,鸡的价钱是 钱,则可列方程组为( )A、 B、 C、 D、9. 下列命题是假命题的是( )A、两条直线被第三条直线所截,如果同位角相等,那么内错角的角平分线互相平行 B、在实数 中,有4个有理数,2个无理数 C、在平面直角坐标系中,点 在 轴上,则点 的坐标为 D、不等式组 的所有整数解的和为710. 如图,三角形 的边 在 轴的正半轴上,点 是原点,点 的坐标为 ,把三角形 沿 轴向右平移2个单位长度,得到三角形 ,连接 ,若三角形 的面积为3,则图中阴影部分的面积为( )
3. 在平面直角坐标系中,点(3,—4)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列调查方式,你认为最合适的是( )A、了解杨家坪步行街每天的流动人口数,采用抽样调查方式 B、旅客上飞机前的安检,采用抽样调查方式 C、了解重庆市居民端午小长假期间的出行方式,采用全面调查方式 D、日光灯管厂要检测一批灯管的使用寿命,采用全面调查方式5. 若 是关于 的二元一次方程 的解,则a的值是( )A、1 B、2 C、3 D、46. 不等式 的最大整数解为 ( )A、2 B、3 C、4 D、57. 估计 的值在下列哪两个整数之间( )A、6和7之间 B、7和8之间 C、8和9之间 D、9和10之间8. 《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术.其中方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有共买鸡,人出八,盈三;人出七,不足四问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,多余3钱,每人出7钱,还缺4钱.问人数和鸡的价钱各是多少?”设人数有 人,鸡的价钱是 钱,则可列方程组为( )A、 B、 C、 D、9. 下列命题是假命题的是( )A、两条直线被第三条直线所截,如果同位角相等,那么内错角的角平分线互相平行 B、在实数 中,有4个有理数,2个无理数 C、在平面直角坐标系中,点 在 轴上,则点 的坐标为 D、不等式组 的所有整数解的和为710. 如图,三角形 的边 在 轴的正半轴上,点 是原点,点 的坐标为 ,把三角形 沿 轴向右平移2个单位长度,得到三角形 ,连接 ,若三角形 的面积为3,则图中阴影部分的面积为( )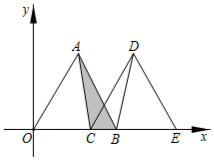 A、 B、1 C、2 D、11. 甲、乙两人分别从 两地同时骑自行车相向而行,2小时后在途中相遇,相遇后,甲、乙骑自行车的速度都提高了1千米/小时,当甲到达地后立刻以原路和提高后的速度向地返行,乙到达 地后也立刻以原路和提高后的速度向 地返行.甲、乙两人在开始 出发后的5小时36分钟又再次相遇,则 两地的距离是( )A、24千米 B、30千米 C、32千米 D、36千米12. 已知 关于的二元一次方程组 的解满足 ,且关于x的不等式组 无解,那么所有符合条件的整数a的个数为( )A、6个 B、7个 C、8个 D、9个
A、 B、1 C、2 D、11. 甲、乙两人分别从 两地同时骑自行车相向而行,2小时后在途中相遇,相遇后,甲、乙骑自行车的速度都提高了1千米/小时,当甲到达地后立刻以原路和提高后的速度向地返行,乙到达 地后也立刻以原路和提高后的速度向 地返行.甲、乙两人在开始 出发后的5小时36分钟又再次相遇,则 两地的距离是( )A、24千米 B、30千米 C、32千米 D、36千米12. 已知 关于的二元一次方程组 的解满足 ,且关于x的不等式组 无解,那么所有符合条件的整数a的个数为( )A、6个 B、7个 C、8个 D、9个二、填空题
-
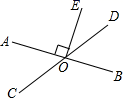
13. 如图,直线 相交于点 为垂足, ,则 度.
 14. 计算: .15. 某超市为了测定某个队付款的等待时间,并经收银台开放方案,统计了这个时间段本超市顾客在收银台排并绘制成如下的频数分布直方图(图中等待时间2分钟到3分钟表示大于或等于2分钟而小于3分钟,其它同类).这个时间段内顾客等待时间不少于6分钟的人数为.
14. 计算: .15. 某超市为了测定某个队付款的等待时间,并经收银台开放方案,统计了这个时间段本超市顾客在收银台排并绘制成如下的频数分布直方图(图中等待时间2分钟到3分钟表示大于或等于2分钟而小于3分钟,其它同类).这个时间段内顾客等待时间不少于6分钟的人数为. 16. 在平面直角坐标系中,点 在第三象限,则 的取值范围是.17. 如图,点A、B为定点,直线l∥AB,P是直线l上一动点,对于下列各值:①线段AB的长;②△PAB的周长;③△PAB的面积;④∠APB的度数,其中不会随点P的移动而变化的是(填写所有正确结论的序号) .
16. 在平面直角坐标系中,点 在第三象限,则 的取值范围是.17. 如图,点A、B为定点,直线l∥AB,P是直线l上一动点,对于下列各值:①线段AB的长;②△PAB的周长;③△PAB的面积;④∠APB的度数,其中不会随点P的移动而变化的是(填写所有正确结论的序号) . 18. 一个农场的工人们要把两片草地的草锄掉,大的一片草地的锄草量是小的一片的两倍.上午半天工人们都在大的一片上锄草,中午后工人们对半分开,一半人留在大的草地上,刚好下午半天就把草锄完了;另一半人到小的草地上去锄草,下午半天锄草后还剩一小块,第二天由一个工人去锄,恰好用了一天时间将草锄完成.如果每一个工人每天锄草量相同,那么这个农场有个工人.
18. 一个农场的工人们要把两片草地的草锄掉,大的一片草地的锄草量是小的一片的两倍.上午半天工人们都在大的一片上锄草,中午后工人们对半分开,一半人留在大的草地上,刚好下午半天就把草锄完了;另一半人到小的草地上去锄草,下午半天锄草后还剩一小块,第二天由一个工人去锄,恰好用了一天时间将草锄完成.如果每一个工人每天锄草量相同,那么这个农场有个工人.三、解答题
-
19.(1)、解方程组: ;(2)、解不等式组: 并把它的解集表示在数轴上.20. 如图, ,点 在直线 上,射线 经过点 ,平分 交 于点 .
 (1)、求证: ;(2)、若 ,求 的度数.21. 如图,在平面直角坐标系中, 的三个顶点的坐标分别为 .
(1)、求证: ;(2)、若 ,求 的度数.21. 如图,在平面直角坐标系中, 的三个顶点的坐标分别为 .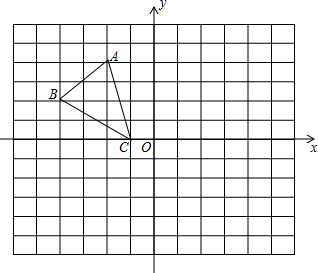 (1)、将 先向右平移3个单位,再向下平移4个单位,则得到 ,请在图中画出 ;(2)、请直接写出点 的坐标;(3)、求出 的面积.22. 某中学积极开展跳绳锻炼,一次体育测试后,体育委员统计了全班同学单位时间的跳绳次数,列出了频数分布表和頻数分布直方图,如图:
(1)、将 先向右平移3个单位,再向下平移4个单位,则得到 ,请在图中画出 ;(2)、请直接写出点 的坐标;(3)、求出 的面积.22. 某中学积极开展跳绳锻炼,一次体育测试后,体育委员统计了全班同学单位时间的跳绳次数,列出了频数分布表和頻数分布直方图,如图:次数
频数
4
18
13
8
1
 (1)、补全频数分布表和频数分布直方图;(2)、表中组距是次,组数是组;(3)、跳绳次数在 范围的学生有人,全班共有人;(4)、若规定跳绳次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?23. 某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.(1)、孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?(2)、某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?(3)、如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?24. 对 定义一种新运算 ,规定: (其中 均为非零常数).例如: .(1)、已知 .
(1)、补全频数分布表和频数分布直方图;(2)、表中组距是次,组数是组;(3)、跳绳次数在 范围的学生有人,全班共有人;(4)、若规定跳绳次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?23. 某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.(1)、孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?(2)、某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?(3)、如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?24. 对 定义一种新运算 ,规定: (其中 均为非零常数).例如: .(1)、已知 .①求 的值;
②若关于 的不等式组 恰好有3个整数解,求 的取值范围;
(2)、当 时, 对任意有理数 都成立,请直接写出 满足的关系式.学习参考:① ,即单项式乘以多项式就是用单项式去乘多项式的每一项,再把所得的结果相加;② ,即多项式乘以多项式就是用一个多项式的每一项去乘另一个多项式的每一项,再把所得的结果相加.
25. 如图,在平面直角坐标系中,长方形 的顶点 分别在 轴、 轴上, 轴, 轴,点 的坐标为 ,且 .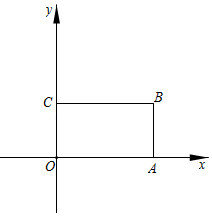 (1)、请直接写出点 的坐标;(2)、若动点 从原点 出发,沿 轴以每秒2个长度单位的速度向右运动,在运动过程中形成的三角形 的面积是长方形 面积的 时,点停止运动,求点 的运动时间;(3)、在(2)的条件下,在 轴上是否存在一点 ,连接 ,使三角形 的面积与长方形 的面积相等?若存在,求出点 的坐标;若不存在,请说明理由.26. 已知, ,点 在 上,点 在 上.
(1)、请直接写出点 的坐标;(2)、若动点 从原点 出发,沿 轴以每秒2个长度单位的速度向右运动,在运动过程中形成的三角形 的面积是长方形 面积的 时,点停止运动,求点 的运动时间;(3)、在(2)的条件下,在 轴上是否存在一点 ,连接 ,使三角形 的面积与长方形 的面积相等?若存在,求出点 的坐标;若不存在,请说明理由.26. 已知, ,点 在 上,点 在 上. (1)、如图1中, 的数量关系为:;(不需要证明)
(1)、如图1中, 的数量关系为:;(不需要证明)如图2中, 的数量关系为:;(不需要证明)
(2)、如图3中, 平分 , 平分 ,且 ,求 的度数;(3)、如图4中, , 平分 , 平分 ,且 ,则 的大小是否发生变化,若变化,请说明理由,若不变化,求出 的度数.