宁夏石嘴山市惠农区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2021-08-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子中正确的是（）

A、 $\sqrt{{(- 13)}^{2}} = - 13$ B、 $\sqrt[3]{- 5} = - \sqrt[3]{5}$ C、 $| 3 - π | = 3 - π$ D、 $\sqrt{9} = \pm 3$

查看试题解析
2. 如图所示，直线AB⊥CD于点O，直线EF经过点O，若∠1＝26°，则∠2的度数是（）

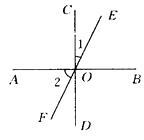A、26° B、64° C、54° D、以上答案都不对

查看试题解析
3. 若 $a > b$ ，则下列各式中不一定成立的是（）

A、 $a - 1 > b - 1$ B、 $\frac{a}{3} > \frac{b}{3}$ C、 $- a < - b$ D、 $a c < b c$

查看试题解析
4. 如图，直线 $l_{1} // l_{2}$ ，则 $∠ α$ 为（）

A、150° B、140° C、130° D、120°

查看试题解析
5. 如图，数轴上有A，B，C，D四点，根据图中各点的位置，判断哪一点所表示的数与， $11 - 2 \sqrt{39}$ 最接近（）

A、A B、B C、C D、D

查看试题解析
6. 下列说法中正确的个数有（）
（ 1 ）直线外一点与直线上各点连接的所有线段中，垂线段最短.

（ 2 ）画一条直线的垂线段可以画无数条.

（ 3 ）在同一平面内，经过一个已知点能画一条且只能画一条直线和已知直线垂直.

（ 4 ）从直线外一点到这条直线的垂线段叫做点到直线的距离.

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 2018年11月贵阳市教育局对某校七年级学生进行体质监测共收集了200名学生的体重，并绘制成了频数分布直方图，从左往右数每个小长方形的长度之比为2:3:4:1，其中第三组的频数为（）

A、 80人 B、60人 C、20人 D、10人

查看试题解析
8. 如图，直线AB和CD相交于O点，OE⊥CD，∠EOF＝142°，∠BOD：∠BOF＝1：3，则∠AOF的度数为（）

A、138° B、128° C、117° D、102°

查看试题解析

二、填空题

9. 如图，已知 $a / / b$ ，李明把三角板的直角顶点放在直线 $b$ 上．若∠1=42°，则∠2的度数为.

查看试题解析
10. 若 $\sqrt{x + 1} + \sqrt{y - 3} = 0$ ，则 $x + y =$ .

查看试题解析
11. 若二元一次方程组 ${\begin{array}{l} x - 2 y = 4 \\ 2 x - y = 3 \end{array}$ 则 $x + y$ 的值为.

查看试题解析
12. 若点（1－2m，m－4）在第三象限内，则m的取值范围是.

查看试题解析
13. 方程 ${(x - 1)}^{3} = \frac{1}{8}$ 的解是.

查看试题解析
14. 如图，在Rt△ABC中，∠C=90°，AC=4，将△ABC沿CB方向平移得到△DEF，若四边形ABED的面积等于8，则平移的距离为．

查看试题解析
15. 如图，在平面直角坐标系中：A(1，1)，B(-1，1)，C(-1，-2)，D(1，-2)，现把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处，并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是.

查看试题解析

三、解答题

16. 解方程式组： ${\begin{array}{l} 5 x - 2 y = 2 \\ x + 3 y = 3 \end{array}$

查看试题解析
17. 解下列不等式组，并把解集在数轴上表示出来. ${\begin{array}{l} 4 x - 7 < 5 (x - 1) \\ \frac{x}{3} \leq 3 - \frac{x - 2}{2} \end{array}$

查看试题解析
18. 已知△ABC三个顶点的坐标分别是 A（﹣3，﹣1）、B（1，3）、C（2，﹣3），

（ 1 ）在平面直角坐标系中描出各点并画出△ABC；

（ 2 ）将△ABC向下平移3个单位，再向右平移2个单位，得到△A′B′C′，画出△A′B′C′；

（ 3 ）求△ABC的面积.

查看试题解析
19. 某校开展了为期一周的“敬老爱亲”社会活动，为了解情况，学生会随机调查了部分学生在这次活动中做家务的时间，并将统计的时间（单位：小时）分成5组，A：0.5≤x＜1，B：1≤x＜1.5，C：1.5≤x＜2，D：2≤x＜2.5，E：2.5≤x＜3，制作成两幅不完整的统计图（如图）.

请根据图中提供的信息，解答下列问题：

(1)、学生会随机调查了名学生；

(2)、补全频数分布直方图；

(3)、若全校有1800名学生，估计该校在这次活动中做家务的时间不少于2.5小时的学生有多少人？

查看试题解析
20. 如图，已知CB∥DE，∠B+∠D＝180°，求证：AB∥CD.

查看试题解析
21. 如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，∠BOD＝35°，求∠CON的度数.

查看试题解析
22. 某社区购买甲、乙两种树苗进行绿化，购买一棵甲种树苗的价钱比购买一棵乙种树苗的价钱多 10 元钱，已知购买 20 棵甲种树苗、30 棵乙种树苗共需 1 200 元钱．

(1)、求购买一棵甲种、一棵乙种树苗各多少元？

(2)、社区决定购买甲、乙两种树苗共 400 棵，总费用不超过 10 600 元，那么该社区最多可以购买多少棵甲种树苗?

查看试题解析
23. 如图，直线EF、CD相交于点O，OA⊥OB，OC平分∠AOF.

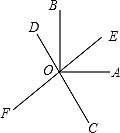(1)、若∠AOE=40°，求∠BOD的度数；

(2)、若∠AOE=30°，请直接写出∠BOD的度数；

(3)、观察(1)(2)的结果，猜想∠AOE和∠BOD的数量关系，并说明理由.

查看试题解析
24. 阅读运用：
当方程中的系数用字母表示时，这样的方程叫做含字母系数的方程，也叫含参数的方程.

例如： $2 x + m = 4$ ，那么如何解这样的方程呢？实际上，我们可以把m当作常数，解出方程，

解得： $2 x = 4 - m$ . $x = \frac{4 - m}{2}$ ，

请仿照上面的解法解答下列问题：

(1)、解关于x，y的二元一次方程组 ${\begin{array}{l} 5 x + 2 y = 5 a \\ 7 x + 4 y = 4 a \end{array}$

(2)、若关于x，y的二元一次方程组： ${\begin{array}{l} 5 x + 2 y = 5 a \\ 7 x + 4 y = 4 a \end{array}$ 的解满足不等式组 ${\begin{matrix} 2 x + y < 5 \\ x - y > - 9 \end{matrix}$ 求出整数a的所有值.

查看试题解析
25. 已知 $A B // C D$ ，点E、F分别在 $A B$ 、 $C D$ 上，点G为平面内一点，连接 $E G$ 、 $F G$ .

(1)、如图，当点G在 $A B$ 、 $C D$ 之间时，请直接写出 $∠ A E G$ 、 $∠ C F G$ 与 $∠ G$ 之间的数量关系.

(2)、如图，当点G在 $A B$ 上方时，且 $∠ E G F = 90^{°}$ ，求证： $∠ B E G - ∠ D F G = 90^{°}$ ；

(3)、如图，在（2）的条件下，过点E作直线 $H K$ 交直线 $C D$ 于K， FT平分 $∠ D F G$ 交 $H K$ 于点T，延长 $G E$ 、 $F T$ 交于点R，若 $∠ E R T = ∠ T E B$ ，请你判断 $F R$ 与 $H K$ 的位置关系，并证明. （不可以直接用三角形内角和180°）

查看试题解析