吉林省白城市四校2020-2021学年高一下学期数学期末考试试卷

试卷更新日期：2021-08-05 类型：期末考试

进入出卷网下载

一、单项选择题（本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 在复平面内，复数 $\frac{1}{1 + 2 i}$ 的共轭复数对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 从2021名学生中选取50名学生参与一项调查，若采用下面的方法选取：先用简单随机抽样从2021人中剔除21人，剩下的2000人再按系统抽样的方法抽取，则每人入选的概率（）

A、不全相等 B、均不相等 C、都相等，且为 $\frac{50}{2021}$ D、都相等，且为 $\frac{1}{40}$

查看试题解析
3. 如图，在 $△ A B C$ 中， $\vec{A N} = \frac{1}{2} \vec{A C}$ ， $P$ 是 $B N$ 的中点，若 $\vec{A P} = m \vec{A B} + \frac{1}{4} \vec{A C}$ ，则实数 $m$ 的值是（）

A、 $\frac{1}{4}$ B、1 C、 $\frac{1}{2}$ D、 $\frac{3}{2}$

查看试题解析
4. 如图，正方形 $O A B C$ 的边长为1，它是水平放置的一个平面图形的直观图，则原图形的面积为（）

A、 $2 \sqrt{2}$ B、1 C、 $\sqrt{2}$ D、 $2 (1 + \sqrt{2})$

查看试题解析
5. 已知 $α \in (\frac{π}{2} ， π)$ ．若 $\cos (\frac{π}{6} - α) = - \frac{\sqrt{2}}{4}$ ，则 $\sin (α + \frac{5 π}{6})$ 的值为（）

A、 $- \frac{\sqrt{2}}{4}$ B、 $\frac{\sqrt{2}}{4}$ C、 $- \frac{\sqrt{14}}{4}$ D、 $\frac{\sqrt{14}}{4}$

查看试题解析
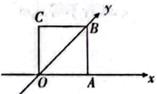6. 在发生某公共卫生事件期间，有专业机构认为该事件在一段时间内没有引起大规模群体感染的标志为“连续10天，每天新增疑似病例不超过7人”．根据过去10天甲、乙、丙、丁四地新增疑似病例数据，一定符合该标志的是（）

A、甲地：总体平均数为3，中位数为4 B、乙地：总体平均数为1，总体方差大于0 C、丙地：中位数为2，众数为3 D、丁地：总体平均数为2，总体方差为3

查看试题解析
7. 已知 $A (- 2 ， 1)$ ， $B (6 ， - 3)$ ， $C (0 ， 5)$ ，则 $△ A B C$ 的形状是（）

A、钝角三角形 B、锐角三角形 C、直角三角形 D、等边三角形

查看试题解析
8. 设偶函数 $f (x)$ 的定义域为R，当 $x \in [0 ， + \infty)$ 时 $f (x)$ 是增函数，则 $f (- 2) ， f (π) ， f (- 3)$ 的大小关系是（）

A、 $f (π) > f (- 3) > f (- 2)$ B、 $f (π) > f (- 2) > f (- 3)$ C、 $f (π) < f (- 3) < f (- 2)$ D、 $f (π) < f (- 2) < f (- 3)$

查看试题解析

二、多项选择题（本大题共4小题，每小题5分，共20分，在每小题给出的四个选项中，有多项符合题目要求全部选对的得5分，部分选对的得3分，有选错的得0分）

9. 设 $m$ ， $n$ 是两条不同的直线， $α$ ， $β$ 是两个不同的平面，下列命题中正确的是（）

A、若 $m ⊥ α$ ， $n // α$ ，则 $m ⊥ n$ B、若 $m // n$ ， $n // α$ ，则 $m // α$ C、若 $m // n$ ， $n ⊥ β$ ， $m // α$ ，则 $α ⊥ β$ D、若 $m ⊥ α$ ， $n ⊥ α$ ，则 $m // n$

查看试题解析
10. 下列函数中是偶函数，且在 $(0 ， + \infty)$ 上为增函数的有（）

A、 $y = \cos x$ B、 $y = x^{3}$ C、 $y = x^{2} + 4$ D、 $y = \log_{2} | x |$

查看试题解析
11. 下列说法错误的是（）

A、若 $\vec{a} // \vec{b}$ ， $\vec{b} // \vec{c}$ ，则 $\vec{a} // \vec{c}$ B、若 $\vec{a} // \vec{b}$ ，则存在唯一实数 $λ$ 使得 $\vec{a} = λ \vec{b}$ C、若 $\vec{a} \cdot \vec{b} = \vec{a} \cdot \vec{c}$ ，且 $\vec{a} \neq 0$ ，则 $\vec{b} = \vec{c}$ D、两个非零向量 $\vec{a}$ ， $\vec{b}$ ，若 $| \vec{a} - \vec{b} | = | \vec{a} | + | \vec{b} |$ ，则 $\vec{a}$ 与 $\vec{b}$ 共线且反向

查看试题解析
12. 已知在正三棱锥 $A - B C D$ 中，底面 $△ B C D$ 的边长为4， $E$ 为 $A D$ 的中点， $A B ⊥ C D$ ， $A B ⊥ C E$ ，下列结论正确的为（）

A、正三棱锥 $A - B C D$ 的体积为 $2 \sqrt{2}$ B、三棱锥 $A - B C D$ 的外接球的表面积为 $24 π$ C、 $A D ⊥ B C$ D、 $C E$ 与 $C D$ 所成角的正切值为 $\frac{3}{4}$

查看试题解析

三、填空题（本大题共4小题，每小题5分，共20分）

13. 设集合 $M = {0 ， 1 ， 2}$ ， $N = {x | x^{2} - 3 x < 0}$ ，则 $M \cap N =$ ．

查看试题解析
14. 从集合 ${2 ， 3 ， \frac{1}{2}}$ 中任取两个不同的数 $a$ ， $b$ ，则 $\log_{a} b > 0$ 的概率为．

查看试题解析
15. 已知向量 $\vec{a} = (2 ， 2)$ ， $\vec{b} = (k ， 1)$ ，且 $\vec{a}$ 与 $\vec{b}$ 的夹角为锐角，则实数 $k$ 的取值范围是．

查看试题解析
16. 如图， $A B C D - A_{1} B_{1} C_{1} D_{1}$ 为正方体，下面结论中正确的是．（把你认为正确的结论都填上）

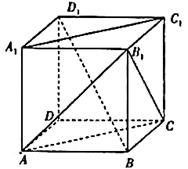
① $A C_{1} ⊥$ 平面 $B D D_{1} B_{1}$ ；

② $B D_{1} ⊥$ 平面 $A C B_{1}$ ；

③ $B D_{1}$ 与平面 $B C C_{1} B_{1}$ 所成角的正切值是 $\sqrt{2}$ ；

④过点 $A_{1}$ 与异面直线 $A D$ 与 $C B_{1}$ 成 $60 °$ 角的直线有2条．

查看试题解析

四、解答题（本大题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤）

17. 已知：复数 $z = {(1 + i)}^{2} + \frac{2 i}{1 - i}$ ，其中 $i$ 为虚数单位．

(1)、求 $z$ 及 $| z |$ ；

(2)、若 $z^{2} + a \bar{z} + b = 2 + 3 i$ ，求实数 $a$ ， $b$ 的值．

查看试题解析
18. 已知向量 $\vec{a}$ ， $\vec{b}$ 满足 $| \vec{a} | = 2$ ， $| \vec{b} | = 1$ ， $(\vec{a} + \vec{b}) \cdot (2 \vec{a} - \vec{b}) = 8$ ．

(1)、求 $\vec{a}$ 与 $\vec{b}$ 的夹角 $θ$ ；

(2)、求 $| \vec{a} + \vec{b} |$ ．

查看试题解析
19. 已知 $A = {x | x^{2} - 2 x - 3 \leq 0}$ ， $B = {x | (x - k) (x - k + 4) > 0}$ ．

(1)、若 $A \cap ∁_{R} B = [0 ， 3]$ ，求实数 $k$ 的值；

(2)、若 $p$ ： $x \in A$ ， $q$ ： $x \in B$ ，若 $p$ 是 $q$ 的充分条件，求实数 $k$ 的取值范围．

查看试题解析
20. 某学校为担任班主任的教师办理手机语音月卡套餐，为了解通话时长，采用随机抽样的方法，得到该校100位班主任每人的月平均通话时长 $T$ （单位：分钟）的数据，其频率分布直方图如图所示，将频率视为概率．

(1)、求图中 $m$ 的值；

(2)、在 $[450 ， 500)$ ， $[500 ， 550]$ 这两组中采用分层抽样的方法抽取6人，再从这6人中随机抽取2人，求抽取的2人恰在同一组的概率．

查看试题解析
21. 如图，已知四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是直角梯形， $A D // B C$ ， $B C = 2 A D$ ， $A D ⊥ C D$ ， $P D ⊥$ 平面 $A B C D$ ， $E$ 为 $P B$ 的中点．

求证：

(1)、若 $C D = P D$ ，证明： $A E ⊥$ 平面 $P B C$ ．

(2)、 $A E //$ 平面 $P D C$ ；

查看试题解析
22. 若向量 $\vec{a} = (\sin x ， \cos x)$ ， $\vec{b} = (\cos x ， - \cos x)$ ， $f (x) = \vec{a} \cdot \vec{b} + t$ 的最大值为 $\frac{\sqrt{2}}{2}$ ．

(1)、求 $t$ 的值及函数的对称中心；

(2)、若不等式 $m^{2} - \frac{1}{2} m \leq f (x)$ 在 $x \in [\frac{π}{4} ， \frac{11 π}{24}]$ 上恒成立，求 $m$ 的取值范围．

查看试题解析