初中数学华师大版九年级上学期第24章 解直角三角形 单元测试
试卷更新日期:2021-08-05 类型:单元试卷
一、单选题
-
1. 下列各组数据是线段的长度,其中,能构成三角形的是( )A、1cm , 2cm , 3cm B、2cm , 3cm , 5cm C、3cm , 4cm , 5cm D、3cm , 3cm , 6cm2. 如图,一棵大树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为( )
 A、6米 B、8米 C、10米 D、12米3. 如图,在 中, ,则 ( )
A、6米 B、8米 C、10米 D、12米3. 如图,在 中, ,则 ( )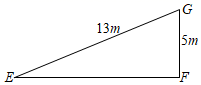 A、 B、 C、 D、4. 矩形ABCD中,对角线AC与BD相交于点O,若∠AOB=60°,AB=v3,则对角线AC的长是( )A、3 B、2 C、3 D、65. 如图,在 中, 按以下步骤作图:分别以点 和 为圆心,大于 的边长为半径作圆弧,两弧相交于点 和 ;作直线 交 于点 ,连结 .若 ,则 的长可能是( )
A、 B、 C、 D、4. 矩形ABCD中,对角线AC与BD相交于点O,若∠AOB=60°,AB=v3,则对角线AC的长是( )A、3 B、2 C、3 D、65. 如图,在 中, 按以下步骤作图:分别以点 和 为圆心,大于 的边长为半径作圆弧,两弧相交于点 和 ;作直线 交 于点 ,连结 .若 ,则 的长可能是( )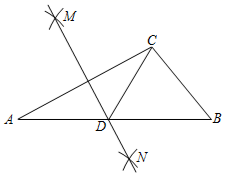 A、 B、 C、 D、6. 如图, 的顶点是正方形网格的格点,则 的值为( )
A、 B、 C、 D、6. 如图, 的顶点是正方形网格的格点,则 的值为( )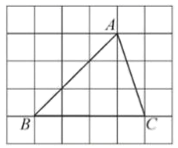 A、 B、 C、 D、7. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )
A、 B、 C、 D、7. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 .据此,可求得学校与工厂之间的距离 等于( )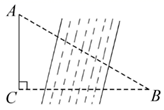 A、 B、 C、 D、8. 如图是一架人字梯,已知 米,AC与地面BC的夹角为 ,则两梯脚之间的距离BC为( )
A、 B、 C、 D、8. 如图是一架人字梯,已知 米,AC与地面BC的夹角为 ,则两梯脚之间的距离BC为( )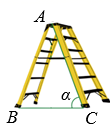 A、 米 B、 米 C、 米 D、 米9. 如图是一张高脚木凳,AC∥EF∥GH,AB=CD,点E,G是AB的三等分点,已知EF与GH之间的距离为25cm,∠EGH=80°,则椅脚AB的长度为 cm( )
A、 米 B、 米 C、 米 D、 米9. 如图是一张高脚木凳,AC∥EF∥GH,AB=CD,点E,G是AB的三等分点,已知EF与GH之间的距离为25cm,∠EGH=80°,则椅脚AB的长度为 cm( ) A、 B、75sin80° C、 D、10. 如图,矩形 中, ,将矩形 绕点 旋转得到矩形 ,使点 的对应点 落在 上, 交 于点 ,在 上取点 ,使 .若 ,则 的长为( )
A、 B、75sin80° C、 D、10. 如图,矩形 中, ,将矩形 绕点 旋转得到矩形 ,使点 的对应点 落在 上, 交 于点 ,在 上取点 ,使 .若 ,则 的长为( )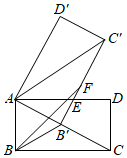 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图所示的正方形网格中有 ,则 的值为 .
 12. 如图,测高仪CD距建筑物底部5m,在测高仪D处观测建筑物顶端的仰角为50°,测高仪高度为1.5m,则建筑物AB的高度为m.(精确到0.1m,sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
12. 如图,测高仪CD距建筑物底部5m,在测高仪D处观测建筑物顶端的仰角为50°,测高仪高度为1.5m,则建筑物AB的高度为m.(精确到0.1m,sin50°≈0.77,cos50°≈0.64,tan50°≈1.19) 13. 将一副直角三角尺按如图所示放置, , , ,则 的长为.
13. 将一副直角三角尺按如图所示放置, , , ,则 的长为. 14. 一条上山直道的坡度为1:7,沿这条直道上山,则前进100米所上升的高度为米.15. 如图,某活动小组利用无人机航拍校园,已知无人机的飞行速度为 ,从A处沿水平方向飞行至B处需 ,同时在地面C处分别测得A处的仰角为 ,B处的仰角为 .则这架无人机的飞行高度大约是 ( ,结果保留整数)
14. 一条上山直道的坡度为1:7,沿这条直道上山,则前进100米所上升的高度为米.15. 如图,某活动小组利用无人机航拍校园,已知无人机的飞行速度为 ,从A处沿水平方向飞行至B处需 ,同时在地面C处分别测得A处的仰角为 ,B处的仰角为 .则这架无人机的飞行高度大约是 ( ,结果保留整数)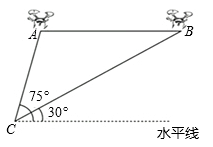 16. 如图,将三角形纸片 折叠,使点 、 都与点 重合,折痕分别为 、 .已知 , , ,则 的长为.
16. 如图,将三角形纸片 折叠,使点 、 都与点 重合,折痕分别为 、 .已知 , , ,则 的长为.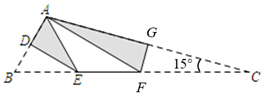 17. 如图,在 中, .点D为 边上一点,将 沿 翻折得到 交 于点E.已知 平分 ,则 .
17. 如图,在 中, .点D为 边上一点,将 沿 翻折得到 交 于点E.已知 平分 ,则 .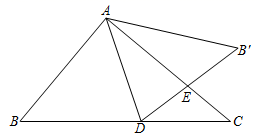
三、解答题
-
18. 如图,在Rt△ABC中,∠B=90°,∠C=30°,AB=4,求BC的长
 19. 有诗云:东山雨霁画屏开,风卷松声入耳来.一座楼阁镇四方,团结一心建家乡.1987年为庆祝湘西自治州成立三十周年,湘西州政府在花果山公园内修建了一座三层楼高的“一心阁”民族团结楼阁.芙蓉学校数学实践活动小组为测量“一心阁” 的高度,在楼前的平地上A处,观测到楼顶 处的仰角为30°,在平地上 处观测到楼顶 处的仰角为 ,并测得A、 两处相距 ,求“一心阁” 的高度.(结果保留小数点后一位,参考数据: , )
19. 有诗云:东山雨霁画屏开,风卷松声入耳来.一座楼阁镇四方,团结一心建家乡.1987年为庆祝湘西自治州成立三十周年,湘西州政府在花果山公园内修建了一座三层楼高的“一心阁”民族团结楼阁.芙蓉学校数学实践活动小组为测量“一心阁” 的高度,在楼前的平地上A处,观测到楼顶 处的仰角为30°,在平地上 处观测到楼顶 处的仰角为 ,并测得A、 两处相距 ,求“一心阁” 的高度.(结果保留小数点后一位,参考数据: , ) 20. 一种千斤顶利用了四边形的不稳定性.如图为一个水平放置的千斤顶,其基本形状是一个菱形,中间通过螺杆连接,转动手柄可改变 的大小(菱形的边长不变),从而改变千斤顶的高度(即 、 之间的距离).若 ,当 从 变为 时,千斤顶升高了多少?( , ,结果保留整数)
20. 一种千斤顶利用了四边形的不稳定性.如图为一个水平放置的千斤顶,其基本形状是一个菱形,中间通过螺杆连接,转动手柄可改变 的大小(菱形的边长不变),从而改变千斤顶的高度(即 、 之间的距离).若 ,当 从 变为 时,千斤顶升高了多少?( , ,结果保留整数)
四、作图题
-
21. 按要求作图(必须用直尺连线):
 (1)、在图①中以点C为位似中心,在网格中画出△DEC,使△DEC与△ABC位似,且△DEC与△ABC的位似比为2:1,(2)、在图②中找到一个格点C,使∠ACB是锐角,且tan∠ACB=1,并画出△ACB.
(1)、在图①中以点C为位似中心,在网格中画出△DEC,使△DEC与△ABC位似,且△DEC与△ABC的位似比为2:1,(2)、在图②中找到一个格点C,使∠ACB是锐角,且tan∠ACB=1,并画出△ACB.五、综合题
-
22. 某种落地灯如图1所示, 为立杆,其高为 ; 为支杆,它可绕点 旋转,其中 长为 ; 为悬杆,滑动悬杆可调节 的长度.支杆 与悬杆 之间的夹角 为 .
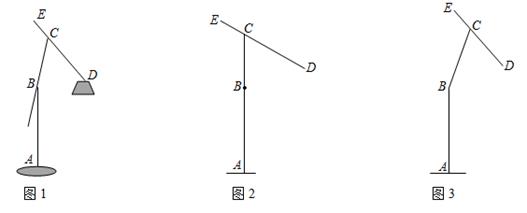 (1)、如图2,当支杆 与地面垂直,且 的长为 时,求灯泡悬挂点 距离地面的高度;(2)、在图2所示的状态下,将支杆 绕点 顺时针旋转 ,同时调节 的长(如图3),此时测得灯泡悬挂点 到地面的距离为 ,求 的长.(结果精确到 ,参考数据: , , , , , )23. 如图,在△ABC中,AB= ,∠B=45°,∠C=60°.
(1)、如图2,当支杆 与地面垂直,且 的长为 时,求灯泡悬挂点 距离地面的高度;(2)、在图2所示的状态下,将支杆 绕点 顺时针旋转 ,同时调节 的长(如图3),此时测得灯泡悬挂点 到地面的距离为 ,求 的长.(结果精确到 ,参考数据: , , , , , )23. 如图,在△ABC中,AB= ,∠B=45°,∠C=60°.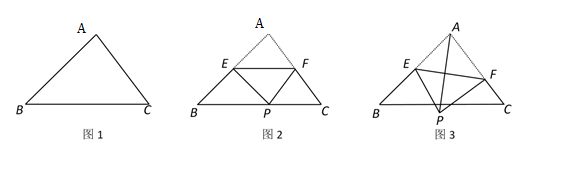 (1)、求BC边上的高线长.(2)、点E为线段AB的中点,点F在边AC上,连结EF , 沿EF将△AEF折叠得到△PEF .
(1)、求BC边上的高线长.(2)、点E为线段AB的中点,点F在边AC上,连结EF , 沿EF将△AEF折叠得到△PEF .①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP , 当PF⊥AC时,求AP的长.
-