初中数学华师大版九年级上学期第24章 24.4 解直角三角形 同步练习
试卷更新日期:2021-08-05 类型:同步测试
一、单选题
-
1. 如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )
 A、2sinα B、2tanα C、2cosα D、
A、2sinα B、2tanα C、2cosα D、 -
2. 如图,某河堤迎水坡AB的坡比 ,堤高 ,则坡面AB的长是( )
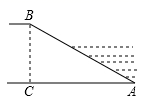 A、5m B、10m C、 m D、8m
A、5m B、10m C、 m D、8m -
3. 关于直角三角形,下列说法正确的是( )A、所有的直角三角形一定相似 B、如果直角三角形的两边长分别是3和4,那么第三边的长一定是5 C、如果已知直角三角形两个元素(直角除外),那么这个直角三角形一定可解 D、如果已知直角三角形一锐角的三角函数值,那么这个直角三角形的三边之比一定确定
-
4. 如图,从点 观测建筑物 的视角是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯 的倾斜角为 ,大厅两层之间的距离 为6米,则自动扶梯 的长约为( )( ).
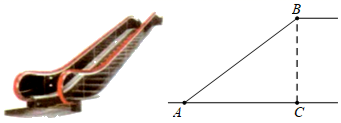 A、7.5米 B、8米 C、9米 D、10米
A、7.5米 B、8米 C、9米 D、10米 -
6. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 . ,则 的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7. 如图,拦水坝的横断面为梯形ABCD.其中 , , ,斜坡AB长8m.则斜坡CD的长为( )
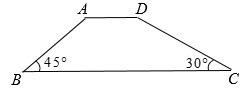 A、 B、 C、 D、
A、 B、 C、 D、 -
8. 如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为 时,梯子顶端靠在墙面上的点 处,底端落在水平地面的点 处,现将梯子底端向墙面靠近,使梯子与地面所成角为 ,已知 ,则梯子顶端上升了( )
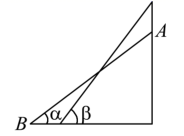 A、1米 B、1.5米 C、2米 D、2.5米
A、1米 B、1.5米 C、2米 D、2.5米 -
9. 小明使用测角仪在甲楼底端A处测得熊猫C处的仰角为53°,在甲楼B处测得熊猫C处的仰角 已知AB=4.5米,则熊猫C处距离地面AD的高度为( )(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
 A、13.6 B、18.1 C、17.3 D、16.8
A、13.6 B、18.1 C、17.3 D、16.8
二、填空题
-
10. 小华从斜坡底端沿斜坡走了100米后,他的垂直高度升高了50米,那么该斜坡的坡角为度
-
11. 平放在地面上的三角形铁板ABC的一部分被沙堆掩埋,其示意图如图所示,量得∠A为54°,∠B为36°,边AB的长为2.1m,BC边上露出部分BD的长为0.6m,则铁板BC边被掩埋部分CD的长是m.(结果精确到0.1m.参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38).

-
12. 如图,有一个小山坡 ,坡比 .已知小山坡的水平距离 ,则小山坡的高度 是.
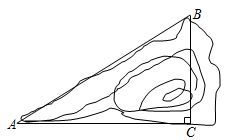
-
13. 如图,一艘轮船位于灯塔P的南偏东 方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东 方向上的B处,此时B处与灯塔P的距离为海里(结果保留根号).
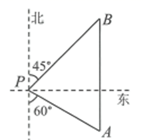
-
14. 高速公路上有一种标线叫纵向减速标线,外号叫鱼骨线,作用是为了提醒驾驶员在开车时减速慢行.如图,用平行四边形 表示一个“鱼骨”, 平行于车辆前行方向, ,过B作 的垂线,垂足为 (A点的视觉错觉点),若 ,则 .

-
15. 如图1是一台手机支架,图2是其侧面示意图, , 可分别绕点A,B转动,测量知 , .当 , 转动到 , 时,点C到 的距离为cm.(结果保留小数点后一位,参考数据: , )
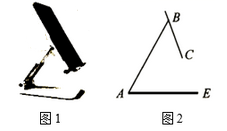
-
16. 某厂家设计一种双层长方体垃圾桶, cm, cm, cm,侧面如图1所示, 为隔板,等分上下两层.下方内桶 绕底部轴 旋转打开,若点 恰好能卡在原来点 的位置,则内桶边 的长度应设计为cm;现将 调整为25cm,打开最大角度时,点 卡在隔板上,如图2所示,可完全放入下方内桶的球体的直径不大于cm.

三、解答题
-
17. 如图,游客从旅游景区山脚下的地面A处出发,沿坡角α=30°的斜坡AB步行50m至山坡B处,乘直立电梯上升30m至C处,再乘缆车沿长为180m的索道CD至山顶D处,此时观测C处的俯角为19°30′,索道CD看作在一条直线上.求山顶D的高度.(精确到1m,sin19°30′≈0.33,cos19°30′≈0.94,tan19°30′≈0.35)
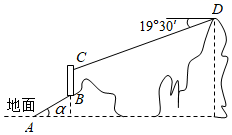
-
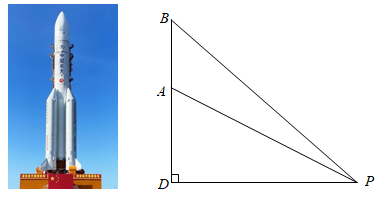
18. 我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角 为 且A与P两点的距离为6千米,它沿铅垂线上升75秒后到达B处,此时在P处测得B点的仰角 为 ,求天舟二号从A处到B处的平均速度.(结果精确到 ,取 )
四、综合题
-
19. 如图,斜坡 的坡角 ,计划在该坡面上安装两排平行的光伏板.前排光伏板的一端位于点 ,过其另一端 安装支架 , 所在的直线垂直于水平线 ,垂足为点 为 与 的交点.已知 ,前排光伏板的坡角 .
参考数据:
三角函数锐角
13°
28°
32°
0.22
0.47
0.53
0.97
0.88
0.85
0.23
0.53
0.62
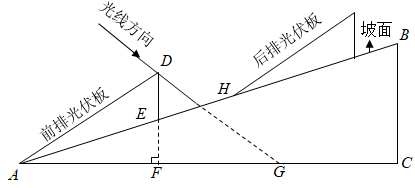 (1)、求 的长(结果取整数);(2)、冬至日正午,经过点 的太阳光线与 所成的角 .后排光伏板的前端 在 上.此时,若要后排光伏板的采光不受前排光伏板的影响,则 的最小值为多少(结果取整数)?
(1)、求 的长(结果取整数);(2)、冬至日正午,经过点 的太阳光线与 所成的角 .后排光伏板的前端 在 上.此时,若要后排光伏板的采光不受前排光伏板的影响,则 的最小值为多少(结果取整数)?
