初中数学华师大版九年级上学期第24章 24.2 直角三角形的性质 同步练习
试卷更新日期:2021-08-05 类型:同步测试
一、单选题
-
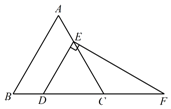
1. 下列各组数中,不可能成为一个三角形的三边的长的一组数是( )A、5,6,7 B、5,7,13 C、5,8,8 D、5,12,132. 下列长度的线段中,与长度为3,5的两条线段能组成三角形的是( )A、2 B、7 C、9 D、113. 图1是一个地铁站入口的双翼闸机.如图2,当双翼收起时,可以通过闸机的物体的最大宽度是64cm,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,此时双翼的边缘AC、BD与闸机侧立面夹角∠PCA=∠BDQ=30°,则双翼的边缘AC、BD(AC=BD)的长度为( )
 A、 cm B、 cm C、27cm D、54cm4. 一个三角形的三边长分别为6,8,11,则这个三角形是( )A、等腰三角形 B、锐角三角形 C、钝角三角形 D、直角三角形5. 如图, 中, 于点D , 若 ,则 的长为( )
A、 cm B、 cm C、27cm D、54cm4. 一个三角形的三边长分别为6,8,11,则这个三角形是( )A、等腰三角形 B、锐角三角形 C、钝角三角形 D、直角三角形5. 如图, 中, 于点D , 若 ,则 的长为( ) A、 B、 C、 D、6. 如图,在矩形ABCD中,对角线AC,BD相交于点O,AC=10,∠ACB=30°,则CD的长为( )
A、 B、 C、 D、6. 如图,在矩形ABCD中,对角线AC,BD相交于点O,AC=10,∠ACB=30°,则CD的长为( )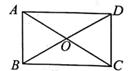 A、5 B、10 C、5 D、57. 如图,在 中, 两顶点 在 轴、 轴上滑动,点 在第一象限内,连接 ,则 的最大值为( )
A、5 B、10 C、5 D、57. 如图,在 中, 两顶点 在 轴、 轴上滑动,点 在第一象限内,连接 ,则 的最大值为( )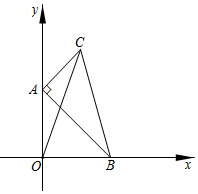 A、7 B、8 C、9 D、8. 已知 、 、为 的三边,且满足 ,则 是( )A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形9. 如图,直角三角板 中, ,一边平行于 的直尺将三角板 分成面积相等的三部分.若 ,则 的长为( )
A、7 B、8 C、9 D、8. 已知 、 、为 的三边,且满足 ,则 是( )A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形9. 如图,直角三角板 中, ,一边平行于 的直尺将三角板 分成面积相等的三部分.若 ,则 的长为( ) A、 B、 C、 D、10. 四边形 中, ,则 的值为( )
A、 B、 C、 D、10. 四边形 中, ,则 的值为( ) A、15 B、 C、 D、20
A、15 B、 C、 D、20二、填空题
-
11. 若长度分别为3,4,a的三条线段能组成一个三角形,则整数a的值可以是.(写出一个即可)12. 三角形三边长分别为3, ,7,则 的取值范围是.13. 如图,Rt△ABC中,∠C=90°,∠A=30°,AB=8cm,则BC=cm.
 14. 如右图,△ABC为等边三角形,DC∥AB,AD⊥CD于D.若△ABC的周长为12 cm,则CD =cm.
14. 如右图,△ABC为等边三角形,DC∥AB,AD⊥CD于D.若△ABC的周长为12 cm,则CD =cm. 15. 一艘快艇的航线如图所示,从O港出发,1小时后到达A地,若快艇的行驶速度保持不变,则快艇驶完AB这段路程的时间为小时。
15. 一艘快艇的航线如图所示,从O港出发,1小时后到达A地,若快艇的行驶速度保持不变,则快艇驶完AB这段路程的时间为小时。 16. 如图,在 中, , ,将 绕点A顺时针旋转 得到 ,直线 、 交于点D,则 的长为.
16. 如图,在 中, , ,将 绕点A顺时针旋转 得到 ,直线 、 交于点D,则 的长为. 17. 如图,在菱形 和菱形 中,点A、B、E在同一直线上,P是线段 的中点,连接 、 .若 ,则 的值为 .
17. 如图,在菱形 和菱形 中,点A、B、E在同一直线上,P是线段 的中点,连接 、 .若 ,则 的值为 .
三、解答题